二叉树OJ练习题（C语言版）

news2024/11/25 6:29:47

目录

 一、相同的树

 二、单值二叉树

 三、对称二叉树

 四、树的遍历

前序遍历

中序遍历

后序遍历

 五、另一颗树的子树

 六、二叉树的遍历

 七、翻转二叉树

 八、平衡二叉树

 一、相同的树

链接：100. 相同的树 - 力扣（LeetCode）

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    if (p == NULL && q == NULL)
        return true;

    if (p == NULL || q == NULL)
        return false;

    if (p->val != q->val)
        return false;

    return isSameTree(p->left, q->left)
        && isSameTree(p->right, q->right);
}
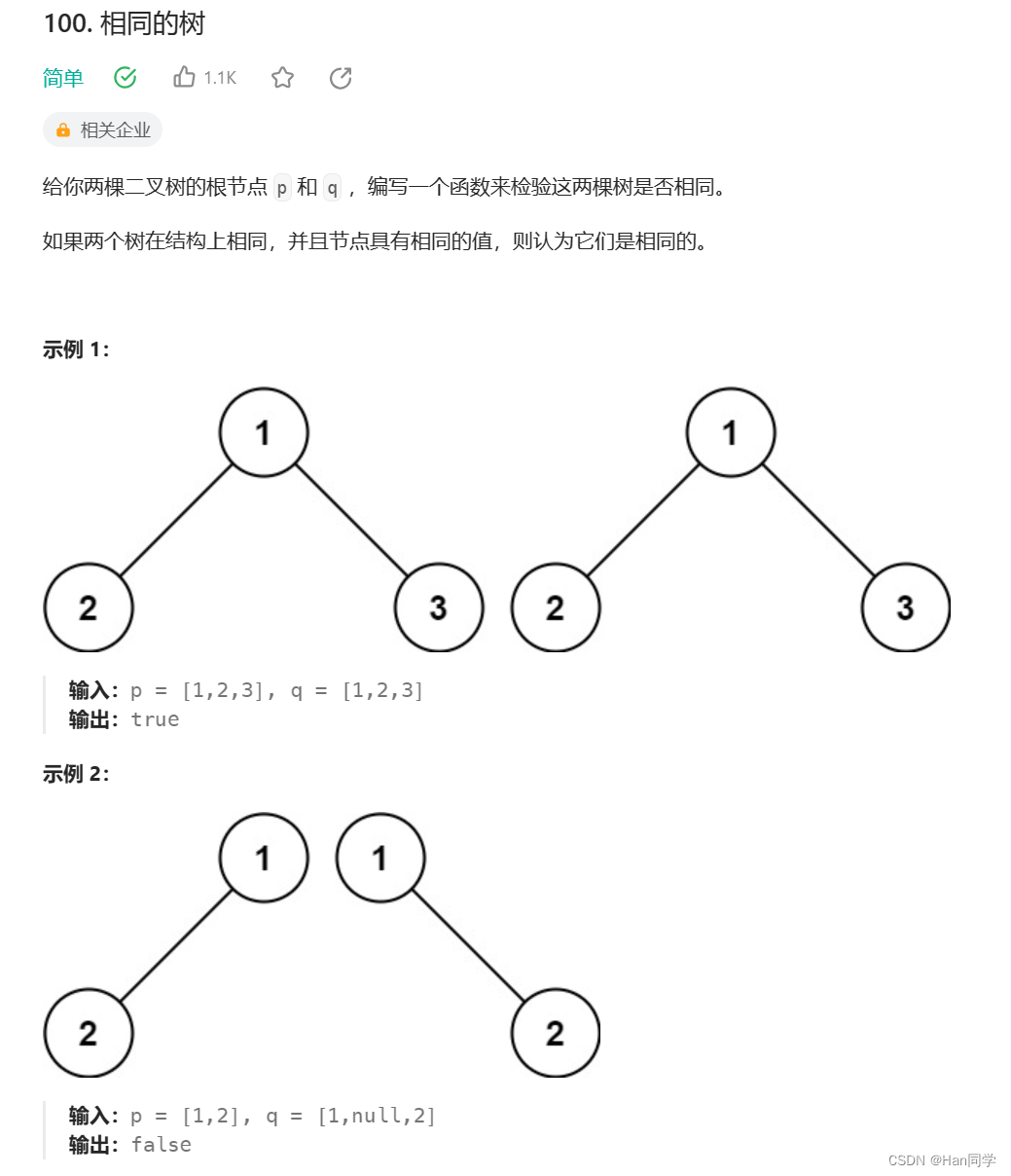
  • 首先考虑比较时节点为空的情况，当比较到二者节点都为空时，则当前二者节点相同，返回true。
  • 二者节点只有一个为空时， 当前二者节点不相同，返回false。
  • 然后考虑不为空时，判断二者的值是否相等，不相等返回false。
  • 最后递归调用比较二者当前节点的左子树和右子树，都为true则返回true。

 二、单值二叉树

链接：965. 单值二叉树 - 力扣（LeetCode）

bool isUnivalTree(struct TreeNode* root) {
    if (root == NULL)
        return true;

    if (root->left && root->left->val != root->val)
        return false;

    if (root->right && root->right->val != root->val)
        return false;

    return isUnivalTree(root->left) &&
        isUnivalTree(root->right);
}
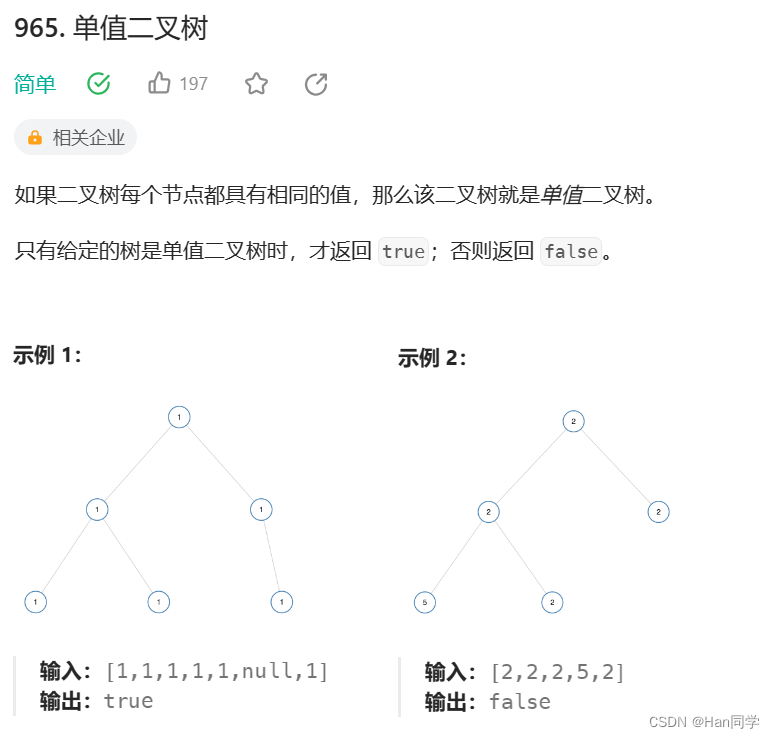
  • 首先判断当前节点是否为空，如果为空则返回true。
  • 如果当前节点不为空，则判断其左右子树的值是否与当前节点的值相同，如果不同则返回false。
  • 如果左右子树的值都与当前节点的值相同，则递归判断左右子树是否为同值二叉树，即左右子树的所有节点的值都相同。
  • 这个递归过程会一直往下遍历到叶子节点，如果所有节点的值都相同，则返回true，否则返回false。

 三、对称二叉树

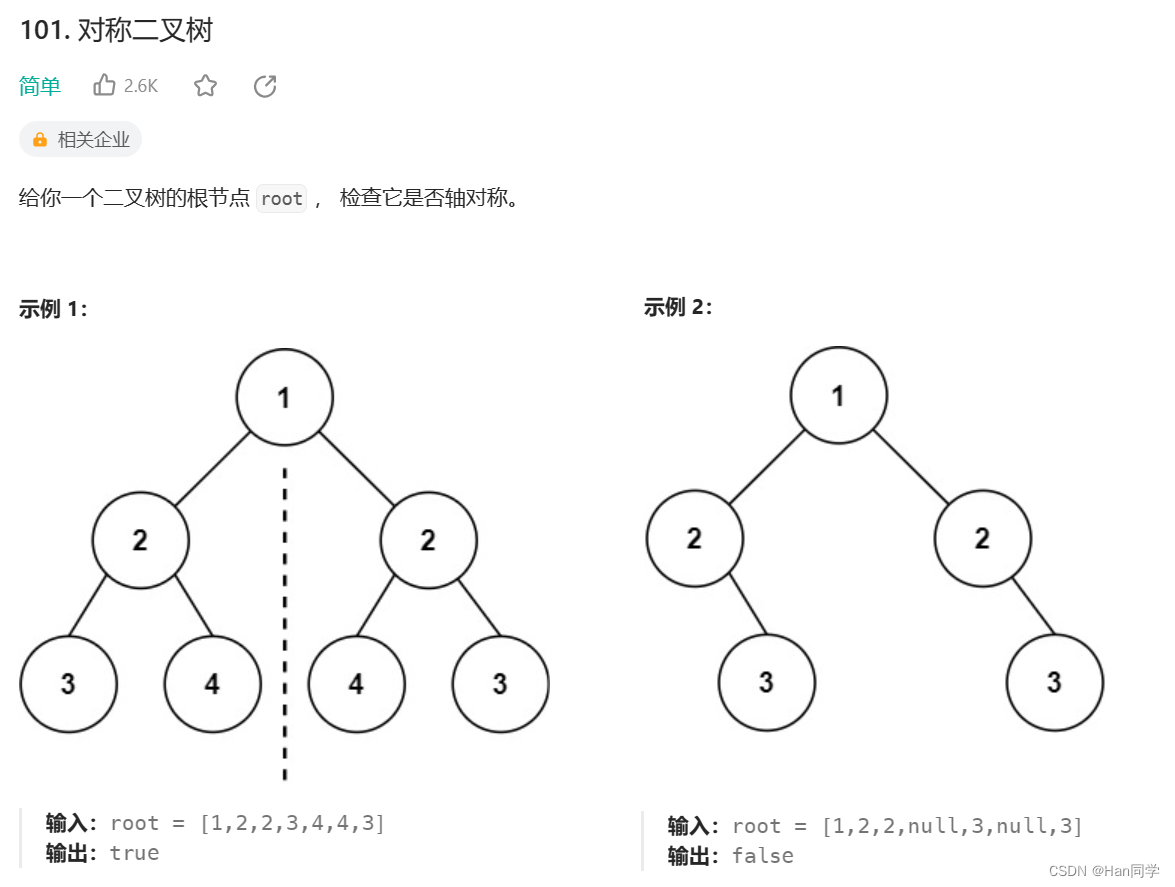
思路：左子树的左节点与右子树的右节点比较，左子树的右节点和右子树的左节点比较

bool _isSymmetric(struct TreeNode* leftRoot, struct TreeNode* rightRoot) {
    if (leftRoot == NULL && rightRoot == NULL)
        return true;
    if (leftRoot == NULL || rightRoot == NULL)
        return false;
    if (leftRoot->val != rightRoot->val)
        return false;
    return _isSymmetric(leftRoot->left, rightRoot->right) 
        && _isSymmetric(leftRoot->right, rightRoot->left);
}

bool isSymmetric(struct TreeNode* root) {
    return _isSymmetric(root->left, root->right);
}

OJ是允许我们额外根据需要创建函数的，原函数的参数只有一个，不能满足同时判断两个节点的是否相等的要求，所以我们创建递归函数_isSymmetric()，用来判断左右子树是否对称。

  • 如果左右子树都为空，说明对称，返回true；
  • 如果左右子树只有一个为空，说明不对称，返回false；
  • 如果左右子树的值不相等，说明不对称，返回false；
  • 否则，递归判断左子树的左子树和右子树的右子树是否对称，以及左子树的右子树和右子树的左子树是否对称，如果都对称，返回true，否则返回false。
  • 函数isSymmetric()则是调用_isSymmetric()函数，传入根节点的左子树和右子树，判断整个二叉树是否对称。

 四、树的遍历

前序遍历

链接：144. 二叉树的前序遍历 - 力扣（LeetCode）

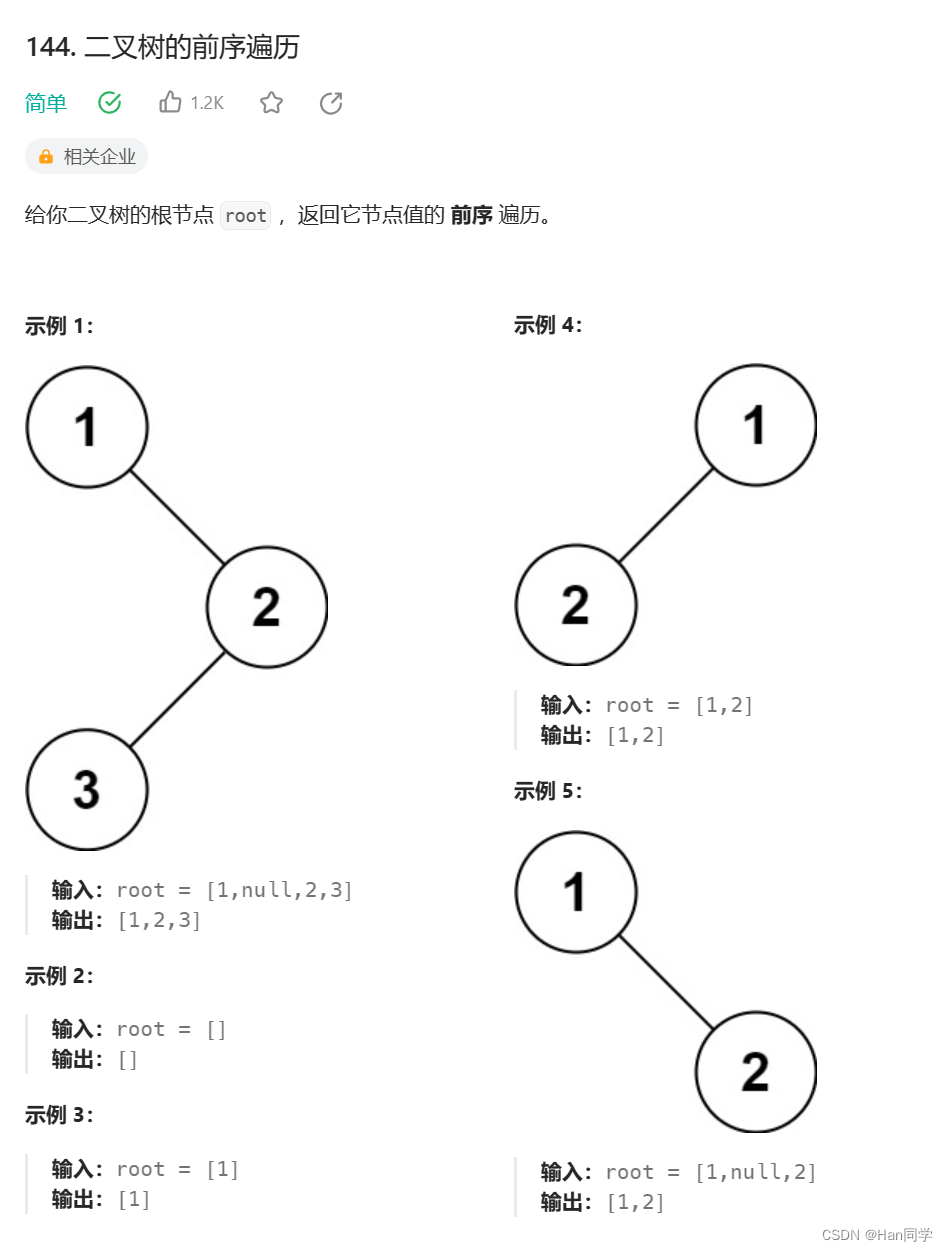
int TreeSize(struct TreeNode* root) {
    return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
void _preorder(struct TreeNode* root, int* a, int* i) {
    if (root == NULL)
        return;
    a[(*i)++] = root->val;
    _preorder(root->left, a, i);
    _preorder(root->right, a, i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
    *returnSize = TreeSize(root);
    int* a = (int*)malloc(*returnSize * sizeof(int));
    int i = 0;
    _preorder(root, a, &i);
    return a;
}

题中要求我们将前序遍历的结果存到数组中并输出数组，那么我们需要创建一个数组插入数据，同时我们也需要数组的大小，所以我们增加了

  • TreeSize函数统计树的节点个数，
  • _preorder递归函数将节点插入数组。

 preorderTraversal函数中：

  • 首先将TreeSize统计的树的大小赋值给returnSize。
  • 为指针a开辟数组所需的空间，用于存放数组元素。
  • 整型变量 i 用于记录数组当前的索引。
  • 调用_preorder函数对数组进行插入数据。
  • 返回数组a。

 _preorder函数中：

  • 如果当前节点为空，则结束函数。
  • 否则，将当前节点的值插入数组中，每次插入结束后，数组的索引值加一。
  • 这里索引参数为指针类型，用于接收索引 i 的地址，这样才能在函数中及时更新索引值。
  • 递归调用_preorder函数对当前节点的左节点进行处理。
  • 左节点处理后，递归调用_preorder函数对当前节点的右节点进行处理。 

中序遍历

94. 二叉树的中序遍历 - 力扣（LeetCode）

int TreeSize(struct TreeNode* root) {
    return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
void _inorder(struct TreeNode* root, int* a, int* i) {
    if (root == NULL)
        return;
    _inorder(root->left, a, i);
    a[(*i)++] = root->val;
    _inorder(root->right, a, i);
}
int* inorderTraversal(struct TreeNode* root, int* returnSize) {
    *returnSize = TreeSize(root);
    int* a = (int*)malloc(*returnSize * sizeof(int));
    int i = 0;
    _inorder(root, a, &i);
    return a;
}

后序遍历

145. 二叉树的后序遍历 - 力扣（LeetCode）

int TreeSize(struct TreeNode* root) {
    return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
void _postorder(struct TreeNode* root, int* a, int* i) {
    if (root == NULL)
        return;
    _postorder(root->left, a, i);
    _postorder(root->right, a, i);
    a[(*i)++] = root->val;
}
int* postorderTraversal(struct TreeNode* root, int* returnSize) {
    *returnSize = TreeSize(root);
    int* a = (int*)malloc(*returnSize * sizeof(int));
    int i = 0;
    _postorder(root, a, &i);
    return a;
}

五、另一颗树的子树

链接：572. 另一棵树的子树 - 力扣（LeetCode）

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    if (p == NULL && q == NULL)
        return true;
    if (p == NULL || q == NULL)
        return false;
    if (p->val != q->val)
        return false;

    return isSameTree(p->left, q->left)
        && isSameTree(p->right, q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {
    if (root == NULL)
        return false;
    
    if (isSameTree(root, subRoot))
        return true;
    
    return isSubtree(root->left, subRoot)
        || isSubtree(root->right, subRoot);
}

调用 isSameTree 辅助判断子树是否相等：

  • 首先考虑比较时节点为空的情况，当比较到二者节点都为空时，则当前二者节点相同，返回true。
  • 二者节点只有一个为空时， 当前二者节点不相同，返回false。
  • 然后考虑不为空时，判断二者的值是否相等，不相等返回false。
  • 最后递归调用比较二者当前节点的左子树和右子树，都为true则返回true。

 isSubtree函数：

  • 如果 root 是 NULL，那么它不可能包含任何子树，函数返回 false。
  • 如果 isSameTree(root, subRoot) 返回 true，说明在当前的节点上，root 和 subRoot 完全相同，那么 subRoot 当然是 root 的子树，函数返回 true。
  • 如果当前节点不匹配，那么递归地在 root 的左子树和右子树中查找 subRoot。
  • 如果 subRoot 是 root 左子树或右子树的子树，函数就返回 true。

 六、二叉树的遍历

链接：二叉树遍历_牛客题霸_牛客网 (nowcoder.com) 

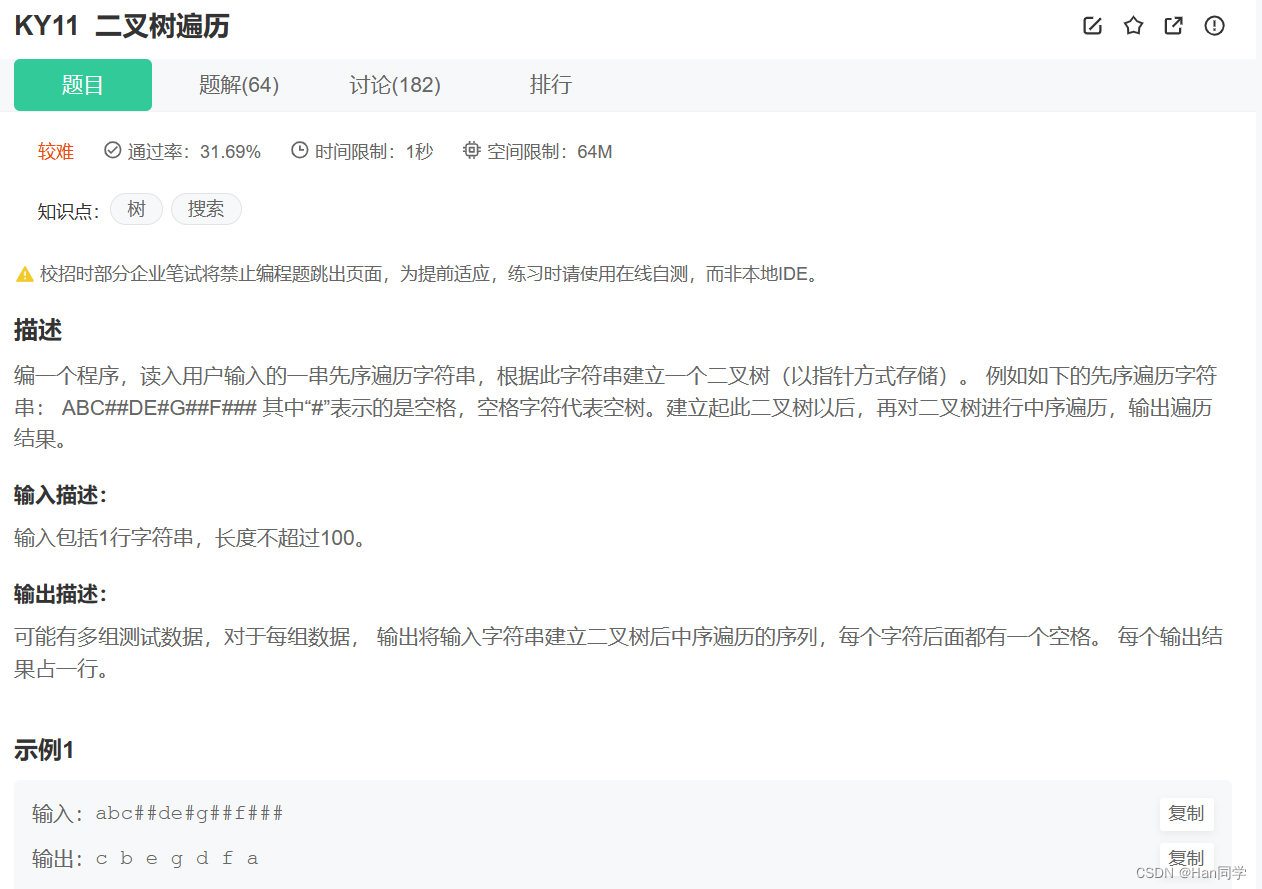
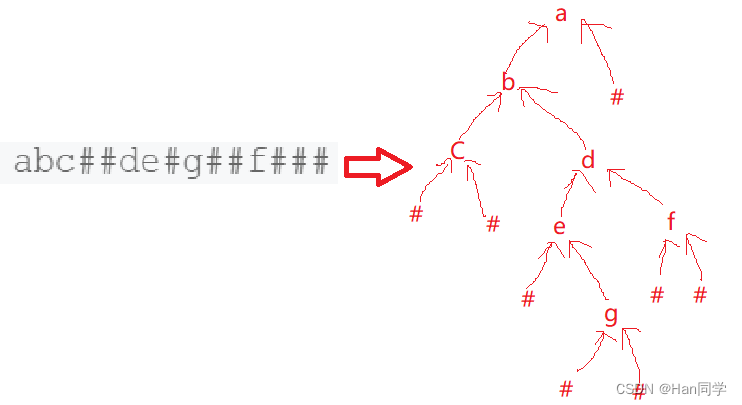
我们需要根据给出的先序(前序)遍历反推出树的样子，例如下图，我们可以动手试一试：

好的，如果你已经熟悉如何根据遍历反推二叉树的形状，那么试着推出题中的遍历的吧。

 注意：这道题需要写出主函数，并不像力扣提供接口。

首先我需要创建二叉树的结构体和相关函数：

#include <stdio.h>
#include <stdlib.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{
    BTDataType data;
    struct BinaryTreeNode* left;
    struct BinaryTreeNode* right;
}BTNode;
BTNode* BuyNode(BTDataType x)
{
    BTNode* node=(BTNode*)malloc(sizeof(BTNode));
    if(node==NULL){
        perror("malloc fail");
        return NULL;
    }
    node->data=x;
    node->left=node->right=NULL;
    return node;
}

然后进行二叉树的创建：

  • 该函数接收两个参数，一个是字符串a，另一个是指向整型变量i的指针，用于记录当前处理到字符串a的哪个位置。
  • 当前位置数组元素为 # 表示元素值为空，更新数组索引到下一个位置，返回NULL
  • 当前位置元素不为空则为其开辟空间，为树创建新节点，更新数组索引到下一个位置。
  • 递归调用CreateTree函数分别创建该节点的左右子树。
  • 最后返回该节点的指针。

在main函数中：

  • 先定义了一个字符数组a，用于存储输入的字符串，
  • 然后调用CreateTree函数创建二叉树，将根节点的指针赋值给root，
  • 最后调用InOrder函数对二叉树进行中序遍历，并输出换行符。
BTNode* CreateTree(char* a,int* i)
{
    if(a[*i]=='#'){
        (*i)++;
        return NULL;
    }
    BTNode* root=BuyNode(a[*i]);
    (*i)++;
    root->left=CreateTree(a, i);
    root->right=CreateTree(a, i);
    return root;
}
void InOrder(BTNode* root)
{
    if(root==NULL)
        return;
    InOrder(root->left);
    printf("%c ",root->data);
    InOrder(root->right);
}
int main() {
    char a[1000];
    scanf("%s",a);
    int i=0;
    BTNode* root=CreateTree(a,&i);
    InOrder(root);
    printf("\n");
    return 0;
}

 七、翻转二叉树

链接：226. 翻转二叉树 - 力扣（LeetCode）

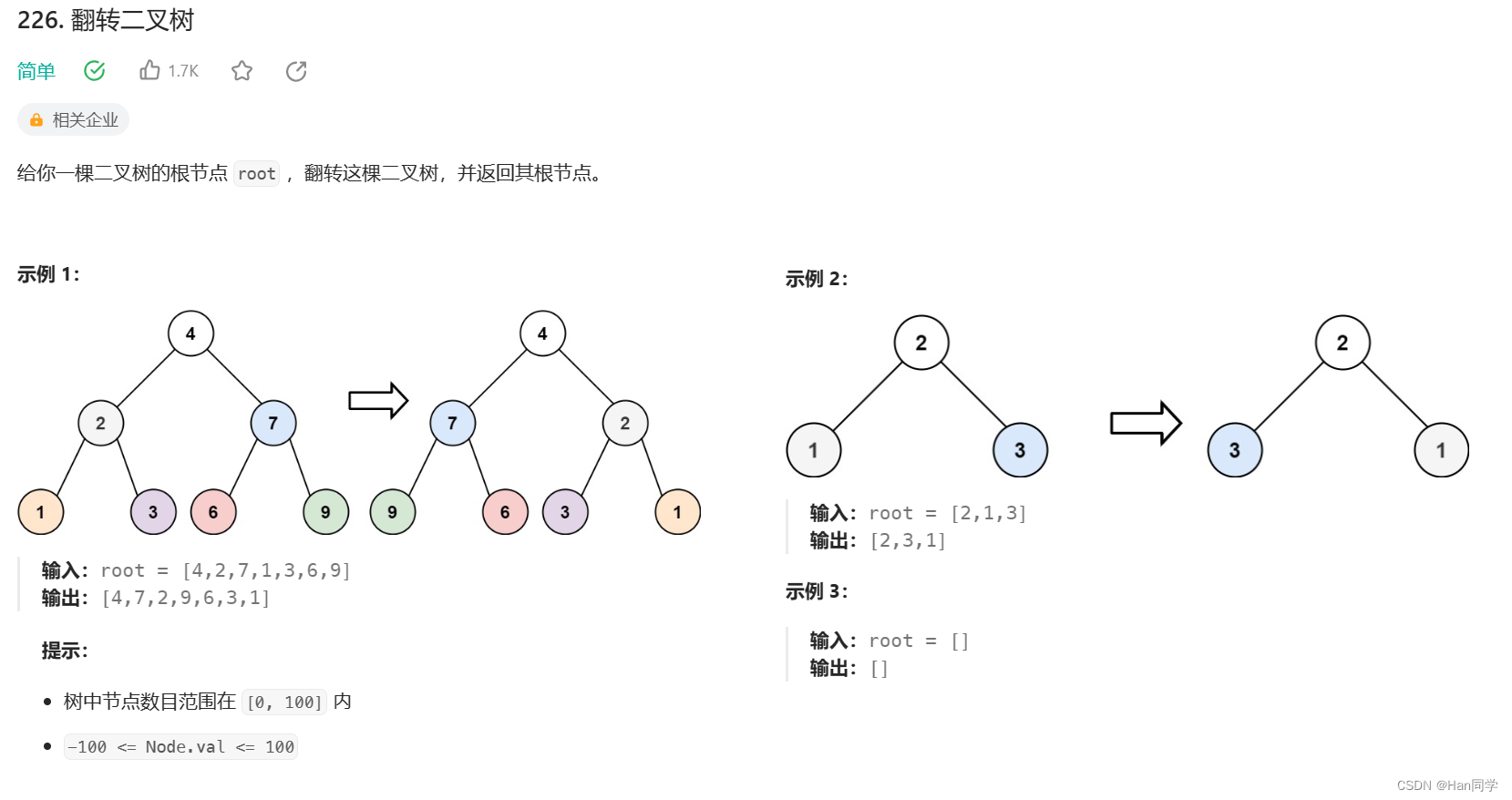
truct TreeNode* invertTree(struct TreeNode* root) {
    if(root==NULL)
        return NULL;
    struct TreeNode* left=invertTree(root->left);
    struct TreeNode* right=invertTree(root->right);
    root->left=right;
    root->right=left;
    return root;
}
  •  如果当前节点为空，则返回NULL.
  • 否则，递归调用函数对左右子树进行处理，递归到二叉树最底部，从最底部往上进行翻转。
  • 将节点的左节点赋值为右节点，右节点赋值为左节点，
  • 最后返回根节点。

八、平衡二叉树

链接：110. 平衡二叉树 - 力扣（LeetCode）

第一种：求出左右子树高度进行判断比较。

  • height函数用于计算二叉树的高度，它采用递归的方式计算左右子树的高度，然后返回左右子树高度的较大值加1，表示当前节点的高度。

  • isBalanced函数则是用于判断二叉树是否平衡，它首先判断当前节点是否为空，如果为空则返回true，否则通过 abs 函数计算左右子树的高度差的绝对值，如果高度差大于1，则返回false，否则递归判断左右子树是否平衡。

int height(struct TreeNode* root){
     if(root == NULL)
	    return 0;
    int leftHeight = height(root->left);
    int rightHeight = height(root->right);
    return leftHeight > rightHeight ?       leftHeight + 1 : rightHeight + 1;
}

bool isBalanced(struct TreeNode* root) {
    if (root == NULL) {
        return true;
    }
    int leftHeight = height(root->left);
    int rightHeight = height(root->right);
    if (abs(leftHeight - rightHeight) > 1) {
        return false;
    }
    return isBalanced(root->left) && isBalanced(root->right);
}

 第二种与第一种功能方法一样，但这种方式更简洁

同样首先写出求树高度的函数，但这里使用三目运算符使函数更简洁。（fmax返回两个参数中较大的那个。）

int maxDepth(struct TreeNode* root){
    return root ? 1 + fmax(maxDepth(root->left) , maxDepth(root->right)) : 0;      
}

bool isBalanced(struct TreeNode* root){
    if(root == NULL)
        return true;
    int left = maxDepth(root->left);
    int right = maxDepth(root->right);
    return abs(left - right) < 2
        && isBalanced(root->left)
        && isBalanced(root->right);
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1173801.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

前端框架Vue学习 ——（一）快速入门

前端框架Vue学习 ——（一）快速入门

文章目录 Vue 介绍Vue快速入门 Vue 介绍 Vue 是一套前端框架&#xff0c;免除原生 JavaScript 中的 DOM 操作&#xff0c;简化书写。基于 MVVM (Model-View-ViewModel)思想&#xff0c;实现数据的双向绑定&#xff0c;将编程的关注点放在数据上。官网: https://v2.cn.vuejs.or…
阅读更多...
Flow-based models(NICE)；流模型+NICE+代码实现

Flow-based models(NICE)；流模型+NICE+代码实现

参考&#xff1a; 李宏毅春季机器学习NICE: Non-linear Independent Components Estimationhttps://github.com/gmum/nice_pytorch 文章目录 大致思想数学预备知识Jacobian矩阵行列式以及其几何意义Change of Variable Theorem Flow-based modelNICE理论代码 大致思想 Flow-B…
阅读更多...
【Linux系统化学习】开发工具——gdb（调试器）

【Linux系统化学习】开发工具——gdb（调试器）

个人主页点击直达&#xff1a;小白不是程序媛 Linux专栏&#xff1a;Linux系统化学习 个人仓库&#xff1a;Gitee 目录 前言&#xff1a; gdb版本检查和安装 Debug和Release gdb的使用 其他指令 前言&#xff1a; 前几篇文章分别介绍了在Linux下的代码编辑器、编译器。…
阅读更多...
c面向对象编码风格（上）

c面向对象编码风格（上）

面向对象和面向过程的基本概念 面向对象和面向过程是两种不同的编程范式&#xff0c;它们在软件开发中用于组织和设计代码的方式。 面向过程编程&#xff08;Procedural Programming&#xff09;是一种以过程&#xff08;函数、方法&#xff09;为核心的编程方式。在面向过程…
阅读更多...
2021年电工杯数学建模B题光伏建筑一体化板块指数发展趋势分析及预测求解全过程论文及程序

2021年电工杯数学建模B题光伏建筑一体化板块指数发展趋势分析及预测求解全过程论文及程序

2021年电工杯数学建模 B题 光伏建筑一体化板块指数发展趋势分析及预测 原题再现&#xff1a; 国家《第十四个五年规划和 2035 年远景目标纲要》中提出&#xff0c;将 2030 年实现“碳达峰”与 2060 年实现“碳中和”作为我国应对全球气候变暖的一个重要远景目标。光伏建筑一体…
阅读更多...
七月论文审稿GPT第二版：从Meta Nougat、GPT4审稿到LongLora版LLaMA、Mistral

七月论文审稿GPT第二版：从Meta Nougat、GPT4审稿到LongLora版LLaMA、Mistral

前言 如此前这篇文章《学术论文GPT的源码解读与微调&#xff1a;从chatpaper、gpt_academic到七月论文审稿GPT》中的第三部分所述&#xff0c;对于论文的摘要/总结、对话、翻译、语法检查而言&#xff0c;市面上的学术论文GPT的效果虽暂未有多好&#xff0c;可至少还过得去&am…
阅读更多...
1.Netty概述

1.Netty概述

原生NIO存在的问题(Netty要解决的问题) 虽然JAVA NIO 和 JAVA AIO框架提供了多路复用IO/异步IO的支持&#xff0c;但是并没有提供给上层“信息格式”的良好封装。JAVA NIO 的 API 使用麻烦,需要熟练掌握 ByteBuffer、Channel、Selector等 , 所以用这些API实现一款真正的网络应…
阅读更多...
题解：轮转数组及复杂度分析

题解：轮转数组及复杂度分析

文章目录 &#x1f349;前言&#x1f349;题目&#x1f34c;解法一&#x1f34c;解法二&#xff1a;以空间换时间&#x1f95d;补充&#xff1a;memmove &#x1f34c;解法三&#xff08;选看&#xff09; &#x1f349;前言 本文侧重对于复杂度的分析&#xff0c;题解为辅。 …
阅读更多...
02-React组件与模块

02-React组件与模块

组件与模块 前期准备 安装React官方浏览器调试工具&#xff0c;浏览器扩展搜索即可 比如红色的React就是本地开发模式 开启一个用React写的网站&#xff0c;比如美团 此时开发状态就变成了蓝色 组件也能解析出来 何为组件&模块 模块&#xff0c;简单来说就是JS代…
阅读更多...
亚马逊云科技大语言模型下的六大创新应用功能

亚马逊云科技大语言模型下的六大创新应用功能

目录 前言 亚马逊云科技的AI创新应用 ​编辑 Amazon CodeWhisperer Amazon CodeWhisperer产品的优势 更快地完成更多工作 自信地进行编码 增强代码安全性 使用收藏夹工具 自定义 CodeWhisperer 以获得更好的建议 如何使用Amazon CodeWhisperer 步骤 1 步骤 2 具体…
阅读更多...
php7.4.32如何快速正确的开启OpenSSL扩展库,最简单的办法在这里!

php7.4.32如何快速正确的开启OpenSSL扩展库,最简单的办法在这里!

&#x1f680; 个人主页 极客小俊 ✍&#x1f3fb; 作者简介&#xff1a;web开发者、设计师、技术分享博主 &#x1f40b; 希望大家多多支持一下, 我们一起进步&#xff01;&#x1f604; &#x1f3c5; 如果文章对你有帮助的话&#xff0c;欢迎评论 &#x1f4ac;点赞&#x1…
阅读更多...
GNU ld链接器 lang_process()(二）

GNU ld链接器 lang_process()(二）

一、ldemul_create_output_section_statements() 位于lang_process()中11行 。 该函数用于创建与目标有关的输出段的语句。这些语句将用于描述输出段的属性和分配。 void ldemul_create_output_section_statements (void) {if (ld_emulation->create_output_section_sta…
阅读更多...
PS Raw中文增效工具Camera Raw 16

PS Raw中文增效工具Camera Raw 16

Camera Raw 16 for mac&#xff08;PS Raw增效工具&#xff09;的功能特色包括强大的图像调整工具。例如&#xff0c;它提供白平衡、曝光、对比度、饱和度等调整选项&#xff0c;帮助用户优化图像的色彩和细节。此外&#xff0c;Camera Raw 16的界面简洁易用&#xff0c;用户可…
阅读更多...
每日一题 187. 重复的DNA序列（中等）

每日一题 187. 重复的DNA序列（中等）

由于今天做了周赛&#xff0c;每日一题就简单点直接暴力哈希 class Solution:def findRepeatedDnaSequences(self, s: str) -> List[str]:d defaultdict(int)ans []for i in range(len(s) - 9):t s[i: i 10]d[t] 1if d[t] 2:ans.append(t)return ans
阅读更多...
CCC数字钥匙设计【NFC】 --通过NFC进行车主配对Phase4

CCC数字钥匙设计【NFC】 --通过NFC进行车主配对Phase4

1、车主配对流程介绍 车主配对可以通过车内NFC进行&#xff0c;若支持UWB测距&#xff0c;也可以通过蓝牙/UWB进行。通过NFC进行车主配对总共有5个Phase。本文档主要对Phase4进行介绍。 1) Phase0&#xff1a;准备阶段&#xff1b; 2) Phase1&#xff1a;启动流程&#xff1…
阅读更多...
凸优化问题（最简单）

凸优化问题（最简单）

一、凸优化问题 1.1 概念 凸优化问题minf(x)&#xff1a;需要同时满足两个条件&#xff1a;变量可行域时凸的(convex)&#xff1b;目标函数也是凸函数(convex)。 &#xff08;1&#xff09;变量x的可行域Ω为凸集&#xff0c;即对于集合Ω中任意两点x1、x2∈Ω&#xff0c;他…
阅读更多...
使用阿里云服务器，httplib库在listen过程中，出现Cannot assign requested address错误？？？

使用阿里云服务器，httplib库在listen过程中，出现Cannot assign requested address错误？？？

今天&#xff0c;在做一个小项目的时候&#xff0c;使用httplib库进行建立tcp连接&#xff0c;但是一旦程序开始&#xff0c;并没有等待tcp连接的到来&#xff0c;而是直接结束了。 打印一下strerror(errno) 根本就没有进行客户端的连接。 找了一下午&#xff0c;检测是否…
阅读更多...
SEO优化的好帮手，5个必备的好工具

SEO优化的好帮手，5个必备的好工具

做海外市场的企业&#xff0c;谷歌SEO是一个非常重要的方式&#xff0c;帮助提高自己企业的网站曝光&#xff0c;起着至关重要的作用&#xff0c;因为人们普遍会通过网上搜索来找到那些适合的商品&#xff0c;与排名靠后的公司相比&#xff0c;出现在搜索结果顶部的公司往往能吸…
阅读更多...
有人物联网模块连接阿里云物联网平台的方法

有人物联网模块连接阿里云物联网平台的方法

摘要&#xff1a;本文介绍有人物联网模块M100连接阿里云的参数设置&#xff0c;作为说明书的补充。 没有阿里云功能需求的请略过本文&#xff0c;不要浪费您宝贵的时间。 网络选择LTE&#xff0c;请先确保插入的SIM卡有流量。 接下来配置阿里云云服务。如下图所示&#xff0c;…
阅读更多...
802.11 CSMA/CA协议

802.11 CSMA/CA协议

《计算机网络自顶向下》P351的总结提炼
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023