今天我们讲一种针对有序数据集合的查找算法:二分查找(Binary Search)算法,也叫折半查找算法。二分查找的思想非常简单,很多非计算机专业的同学很容易就能理解,但是看似越简单的东西往往越难掌握好,想要灵活应用就更加困难。
老规矩,我们还是来看一道思考题。
假设我们有1000万个整数数据,每个数据占8个字节,如何设计数据结构和算法,快速判断某个整数是否出现在这1000万数据中? 我们希望这个功能不要占用太多的内存空间,最多不要超过100MB,你会怎么做呢?带着这个问题,让我们进入今天的内容吧!
无处不在的二分思想
二分查找是一种非常简单易懂的快速查找算法,生活中到处可见。比如说,我们现在来做一个猜字游戏。我随机写一个0到99之间的数字,然后你来猜我写的是什么。猜的过程中,你每猜一次,我就会告诉你猜的大了还是小了,直到猜中为止。你来想想,如何快速猜中我写的数字呢?
假设我写的数字是23,你可以按照下面的步骤来试一试。(如果猜测范围的数字有偶数个,中间数有两个,就选择较小的那个。)
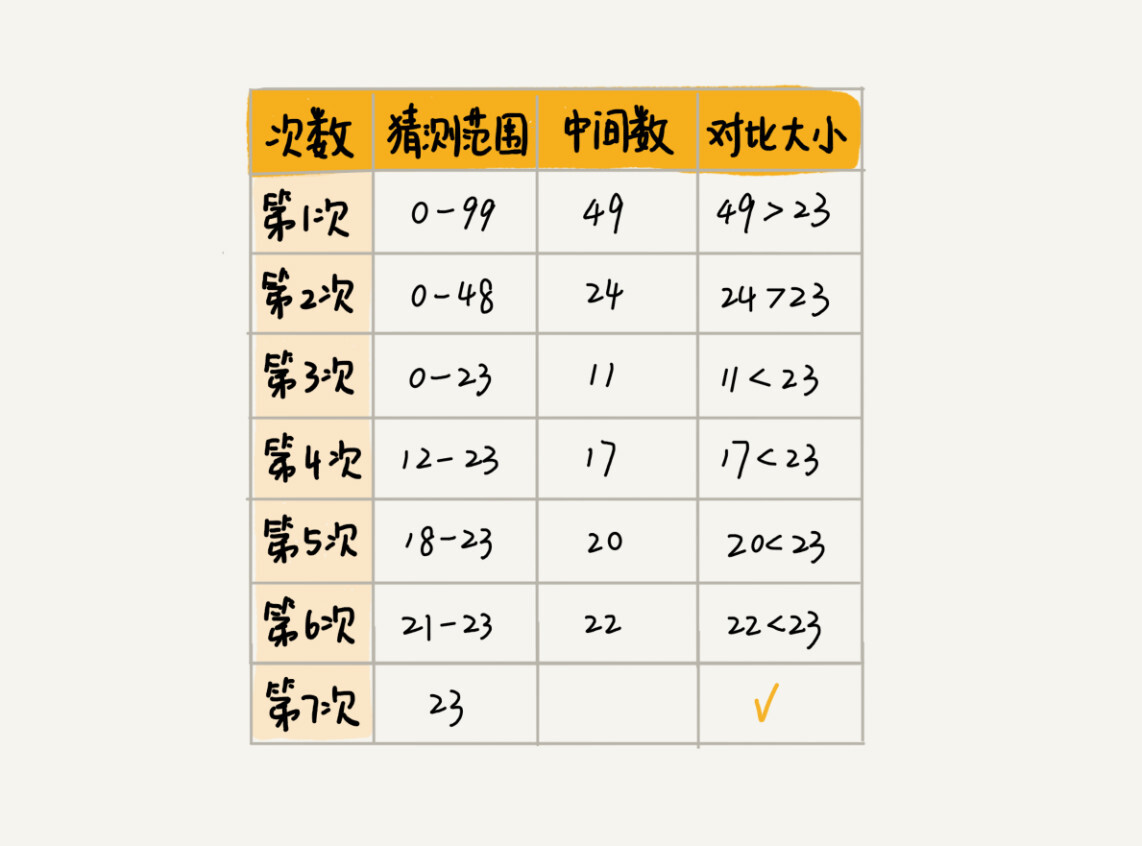
7次就猜出来了,是不是很快?这个例子用的就是二分思想,按照这个思想,即便我让你猜的是0到999的数字,最多也只要10次就能猜中。不信的话,你可以试一试。
这是一个生活中的例子,我们现在回到实际的开发场景中。假设有1000条订单数据,已经按照订单金额从小到大排序,每个订单金额都不同,并且最小单位是元。我们现在想知道是否存在金额等于19元的订单。如果存在,则返回订单数据,如果不存在则返回null。
最简单的办法当然是从第一个订单开始,一个一个遍历这1000个订单,直到找到金额等于19元的订单为止。但这样查找会比较慢,最坏情况下,可能要遍历完这1000条记录才能找到。那用二分查找能不能更快速地解决呢?
为了方便讲解,我们假设只有10个订单,订单金额分别是:8,11,19,23,27,33,45,55,67,98。
还是利用二分思想,每次都与区间的中间数据比对大小,缩小查找区间的范围。为了更加直观,我画了一张查找过程的图。其中,low和high表示待查找区间的下标,mid表示待查找区间的中间元素下标。