文章目录
- 🍉前言
- 🍉题目
- 🍌解法一
- 🍌解法二:以空间换时间
- 🥝补充:memmove
- 🍌解法三(选看)
🍉前言
本文侧重对于复杂度的分析,题解为辅。
🍉题目
🍌解法一
最简单的思路就是写个循环,每次移动一次,移动k次。得到如下代码:
void rotate(int* nums, int numsSize, int k) {
for(int i = 0;i < k;i++) {
int tmp = nums[numsSize-1]; //保存最后一个元素
for(int j = numsSize-2;j >= 0;j--) {
nums[j+1] = nums[j]; //从后往前覆盖
}
nums[0] = tmp; //原本最后一个元素的值给到现在第一个元素
}
}
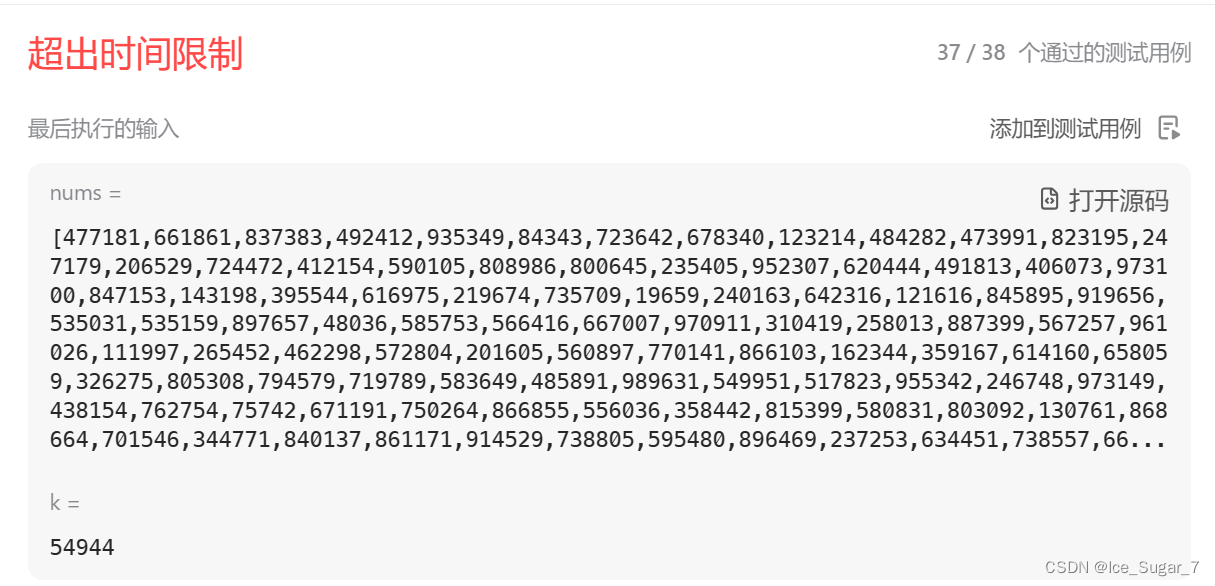
当你以为已经完成了,兴冲冲跑去提交的代码的时候,意外发生了:
啊?超时了!!!
这就涉及到时间复杂度的问题了,来分析一下上面的算法:
你可能会这样认为:外层循环走了k次,而由于numsSize是变量,把它看为n的话,就相当于内层循环跑了(n-1)次,那么总共就跑了k*(n-1)次,时间复杂度就为O(n)咯。
但是,你忽略了k,你以为它是一个常数,而它又是n的系数,就把它给忽略了。实际上k也是一个变量。按照时间复杂度取最坏的情况,我们来思考一下:每次移动一个单位,在什么情况下需要移动的次数最多?
在此我们要考虑“净轮转”,比如数组长度为6,那你往右轮转11个单位和轮转5个单位是等效的。
那显然,最坏的情况就是你轮转的k为(n-1)个单位,结合上面分析,可知时间复杂度为O(n^2)。
🍌解法二:以空间换时间
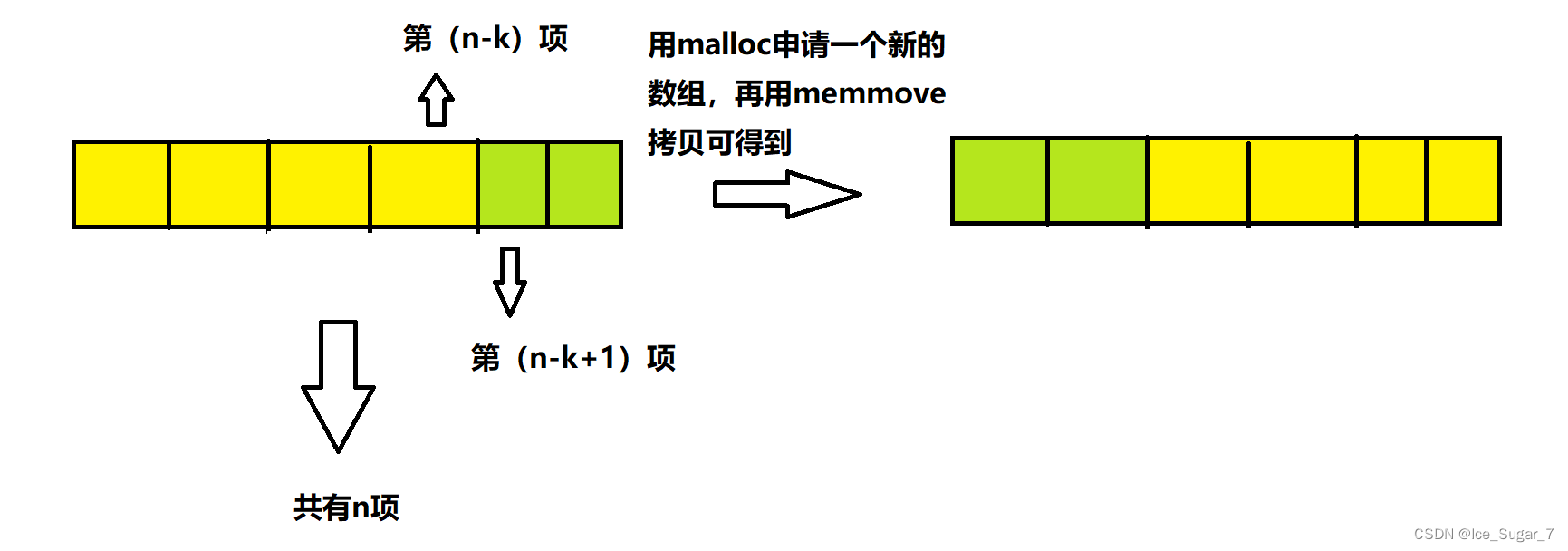
void rotate(int* nums, int numsSize, int k) {
k %= numsSize;
int* arr = (int*)malloc(sizeof(int)*numsSize);
memmove(arr,nums+numsSize-k,sizeof(int)*k);
memmove(arr+k,nums,sizeof(int)*(numsSize-k));
memmove(nums,arr,sizeof(int)*numsSize);
}
注意:这个题有个小坑,就是题干给的k没有限定范围,当k超过数组长度的时候使用memmove拷贝就会越界,所以在一开始就 k %= numsSize,这样处理后的 k 就是“净轮转”的位置
看到这里你可能想说:你上面解法一超时会不会是因为k没模numSize,移动次数太多导致超时了?确实是一部分原因,但只是特别小的一部分,更多的还是因为那个算法时间复杂度出问题。(其实我也有去试过模个numSize,可还是超时了)
不扯太远了,我们来观察一下,这个算法相比于解法一,时间复杂度降低了一一变为O(n),这就是一个很大的进步了,但是由于额外开辟一块空间,现在空间复杂度变为O(n)了(原先解法一是O(1))。这就是典型的以时间换空间,以后还会经常见到这种思想的。
🥝补充:memmove
memmove(目标地址,起始地址,拷贝的空间的大小)
若起始地址指向的空间和目标地址指向的空间有相互覆盖的部分,memmove也可以实现拷贝(虽然memcpy也可以,但我们一般还是用memmove)
🍌解法三(选看)
实际上本题还有有一个进阶的要求:要求算法空间复杂度为O(1)。
那这时候显然解法二不满足要求了。
所以有一个比较考验数学功底的解法:将要移动的和不移动的分为两部分,先将它们分别倒置,然后再整体倒置。
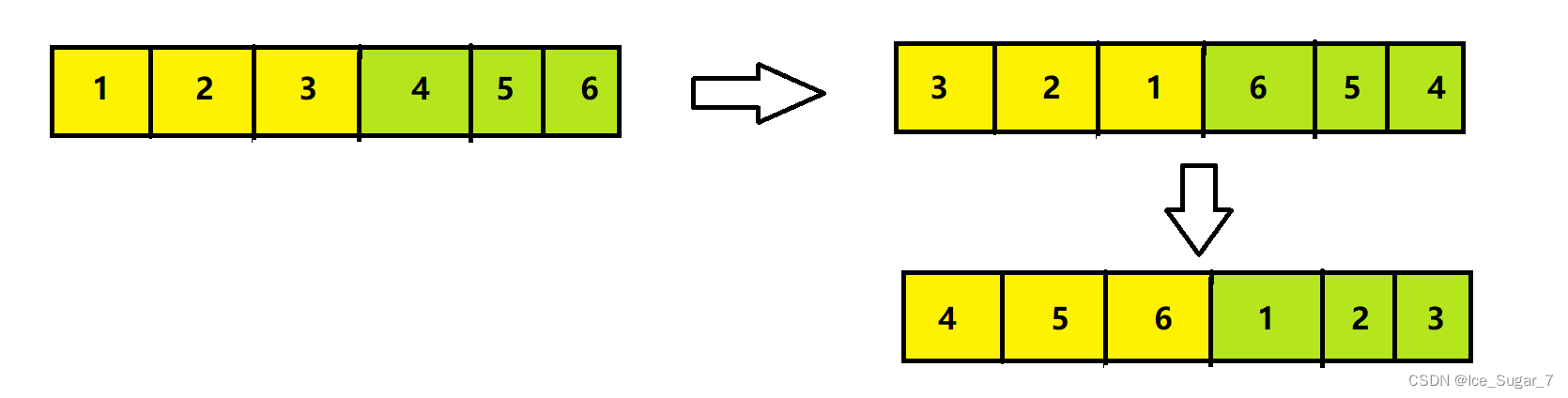
不过这种解法一般人真的很难想得到,普适性太低,所以在此不写代码演示了。