1.土地分割
【问题描述】
对于一块m×n 的地块,需要将其划分为若干个相同正方形的方块,且每个方块的边长尽量地长。
【输入形式】
输入 m 和 n ( 1 ≤ m、 n ≤0.5×109), 分别表示地块的长和宽。
【输出形式】
输出两个整数,表示划分以后的正方形的个数以及边长。
【样例输入】
1680 640
【样例输出】
168 80
//土地分割
//对于一块m×n 的地块,需要将其划分为若干个相同正方形的方块,且每个方块的边长尽量地长。
#include<iostream>
using namespace std;
int gcd(int,int);
int main()
{
int m,n;
cin>>m>>n;
int t1=m,t2=n;
long long res=gcd(m,n);
long long count=t1/res; //防止数据溢出
count=count*t2/res;
cout<<count<<" "<<res;
return 0;
}
int gcd(int m,int n)
{
if(n==0){
return m;
}else{
return gcd(n,m%n); //求最大公约数
}
}
2.过河卒
【问题描述】
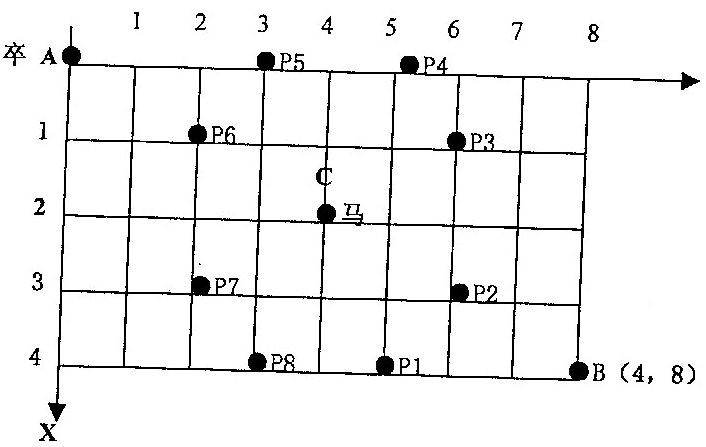
如图,A 点有一个过河卒,需要走到目标 B 点。卒行走规则:可以向下、或者向右。同时在棋盘上的任一点有一个对方的马(图中的C点),该马所在的点和所有跳跃一步可达的点称为对方马的控制点(中国象棋规定马走“日”字)。例如图中 C 点上的马可以控制 9 个点(图中的P1,P2 … P8 和 C)。卒不能通过对方马的控制点。
棋盘用坐标表示,A 点(0,0)、B 点(n,m)(n,m 为不超过 20 的整数,并由键盘输入),同样马的位置坐标是需要给出的(约定: C不等于A,同时C不等于B)。现在要求你计算出卒从 A 点能够到达 B 点的路径的条数。
【输入形式】
输入一行4个整数,分别表示B点的坐标(n,m)以及对方马的坐标(X,Y)
【输出形式】
输出一个整数,表示路径的条数
【样例输入】
6 6 3 2
【样例输出】
17
//过河卒
//A 点有一个过河卒,需要走到目标 B 点。卒行走规则:可以向下、或者向右。同时在棋盘上的任一点有一个对方的马(图中的C点),该马所在的点和所有跳跃一步可达的点称为对方马的控制点(中国象棋规定马走“日”字)。例如图中 C 点上的马可以控制 9 个点(图中的P1,P2 … P8 和 C)。卒不能通过对方马的控制点。
//
// 棋盘用坐标表示,A 点(0,0)、B 点(n,m)(n,m 为不超过 20 的整数,并由键盘输入),同样马的位置坐标是需要给出的(约定: C不等于A,同时C不等于B)。现在要求你计算出卒从 A 点能够到达 B 点的路径的条数。
#include<iostream>
using namespace std;
int path[30][30];
int main()
{
int n,m,x,y;
cin>>n>>m>>x>>y;
for(int i=0;i<=n;i++){
for(int j=0;j<=m;j++){
path[i][j]=1; //初始化path[i][j]表示到达该位置的方法数
}
}
if(x<n&&y<m-1)path[x+1][y+2]=0;
if(x<n&&y>1)path[x+1][y-2]=0;
if(x>0&&y<m-1)path[x-1][y+2]=0;
if(x>0&&y>1)path[x-1][y-2]=0;
if(x<n-1&&y<m)path[x+2][y+1]=0;
if(x<n-1&&y>0)path[x+2][y-1]=0;
if(x>1&&y<m)path[x-2][y+1]=0;
if(x>1&&y>0)path[x-2][y-1]=0; //列出所有不可以到达的位置置为0
path[x][y]=0;
for(int i=0;i<=n;i++){
for(int j=0;j<=m;j++){
if(path[i][j]==0){
continue;
}
if(i==0&&j==0){
continue;
}
if(i==0){
path[i][j]=path[i][j-1]; //就等于左边格子的方法数
}
if(j==0){
path[i][j]=path[i-1][j]; //等于上边格子方法数
}
if(i>=1&&j>=1 && path[i][j]!=0){
path[i][j]=path[i-1][j]+path[i][j-1]; //到达该位置的方法数等于到达其左边和上方方法数之和
}
}
}
cout<<path[n][m];
return 0;
}3.余数运算
【问题描述】
模运算,即求余运算,是数论中的重要内容,在加密领域有非常重要的应用,其运算公式为 ab mod p, 其中 a、b、p 均为正整数,输入a、b、p 的值,求上述运算的结果,建议用递归实现。
提示,x mod y等同于 x % y , 即求 x 除以 y 的余数。
【输入形式】
输入为一行三个数a、b、p (1≤a、p ≤1000,1≤ b <10000)
【输出形式】
输出为一个整数。
【样例输入1】
312 53 333
【样例输出1】
81
【样例输入2】
3 5 8
【样例输出2】
3
//余数运算
//模运算,即求余运算,是数论中的重要内容,在加密领域有非常重要的应用,其运算公式为 ab mod p, 其中 a、b、p 均为正整数,输入a、b、p 的值,求上述运算的结果,建议用递归实现。
// 提示,x mod y等同于 x % y , 即求 x 除以 y 的余数。
#include<iostream>
using namespace std;
typedef long long int ll;
ll getMod(ll a, ll b, ll p);
int main()
{
ll a, b, p;
cin>>a>>b>>p;
ll ans=getMod(a,b,p);///(a * b) mod n = (a mod n * b mod n) mod n
ans=ans%p;
cout<<ans<<endl;
return 0;
}
ll getMod(ll a, ll b, ll p)
{
int tem=a;//记录原值
a=a%p;
for(int i=1;i<b;i++){
a=a*tem%p;
}
return a;
}4.最大连续和
【问题描述】
对于一个具有 n 个元素的整型数组 a,求具有最大连续和的子数组(最少具有一个元素)。
【输入形式】
输入的第一行为一个整数 n ,接下来的一行为 n 个整数,表示数组的元素。
【输出形式】
输出具有最大连续和的子数组的起始编号和结束编号(数组编号为0~n-1)。
【样例输入】
8 3 -5 1 5 -4 12 0 -1
【样例输出】
2 5
//最大连续和
//对于一个具有 n 个元素的整型数组 a,求具有最大连续和的子数组(最少具有一个元素)。
# include <iostream>
using namespace std;
void getMaxSum(int a[], int n, int &Left, int &Right);
int main()
{
int n;
cin>>n;
int *p=new int[n];
for(int i=0; i<n; i++)
cin>>p[i];
int Left, Right;
getMaxSum(p,n,Left,Right);
cout<<Left<<" "<<Right<<endl;
delete[] p;
return 0;
}
void getMaxSum(int a[], int n, int &Left, int &Right)
{
int *dp=new int[n]; //dp[i]表示以i结尾的最大连续和
int m=dp[0];
Left=0;
Right=0;
for(int i=0;i<n;i++){
dp[i]=a[i];//初始化
}
for(int i=1;i<n;i++){
if(dp[i-1]+a[i]>a[i]){
dp[i]=dp[i-1]+a[i]; //要么加上前面的,要么只有自己
}else{
dp[i]=a[i];
}
if(dp[i]>m){
Right=i; //右边界
m=dp[i];
}
}
for(int i=Right;i>=0;i--){
m-=a[i];
if(m==0){
Left=i; //找到左边界
break;
}
}
}