归并排序
- 前言
- 一、归并排序递归实现
- (1)归并排序的核心思路
- (2)归并排序实现的核心步骤
- (3)归并排序码源详解
- (4)归并排序效率分析
- 1)时间复杂度 O(N*logN)
- 2)空间复杂度 O(N)
- 稳定性:稳定
- 二、归并排序的非递归实现
- (1) 关于递归的缺点的讨论
- (2) 归并排序 非递归算法实现思路
- (3)码源详解
- (4)运行结果
前言
快速排序:前序
归并排序:后序
一、归并排序递归实现
(1)归并排序的核心思路
将 已有序的子序列 合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
(2)归并排序实现的核心步骤
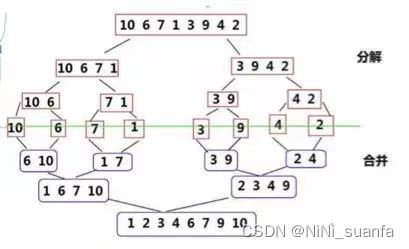
- 向下递归 对半分割 。
- 递归返回条件:递归到最小,1个即是有序 [ 控制的是范围 归并的区间 ]
- 递归到最深处,最小时,就递归回去,开始分按对半分割分出的范围, 将 已有序的子序列 合并,在 tmp 里进行归并。
- 再将tmp里形成的有序序列,拷贝回原数组 【 因为下一次递归回去上一层再进行下一次的归并过程中,会将数据在tmp中进行归并,会将tmp中的数据覆盖,所以要及时将小部分已归并排好序的子序列拷贝回原数组 】
- 再进行递归返回上一层的递归归并,直到递归层数都结束。
(3)归并排序码源详解
void _MergeSort(DataType* a, DataType* tmp, int begin, int end) {
if (begin>=end) { //递归返回的条件:不正常的的范围 或 只剩1个数
return;
}
int mid = (begin + end) / 2;
//先递归到最小
//[begin,mid][mid+1,end]
_MergeSort(a, tmp, begin, mid); //数组是从0开始,所以end=mid-1这样设计
_MergeSort(a, tmp, mid+1, end);
//再进行归并 —— 所以归并的过程,设计在递归后面(后序)
//归并到tmp数组,再拷贝回去
int begin1 = begin; int end1 = mid;
int begin2 = mid + 1; int end2 = end;
int index = begin; //指向tmp,=begin是 根据要进行比较插入的数组的位置 找到其对应在tmp中所对应的位置,则不会覆盖前面已经排好序的数据
//原型:合并两组数,且有序
while (begin1 <= end1 && begin2 <= end2) { //&&其中一组满足了条件就不再继续,就跳出循环
if (a[begin1] < a[begin2]) {
tmp[index++] = a[begin1++];
}
else {
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1) { //把剩下还没插入tmp的,插入进去
tmp[index++] = a[begin1++];
}
while (begin2 <= end2) { //把剩下还没插入tmp的,插入进去
tmp[index++] = a[begin2++];
}
//拷贝回原数组
//source dest 拷贝的数组大小
memcpy(a+begin,tmp+begin,sizeof(DataType)*(end-begin+1));
}
void MergeSort(DataType* a, int n) {
DataType* tmp = (DataType*)malloc(sizeof(DataType) * n); //开辟新的数组(临时存放)用于归并排序过程
if (tmp == NULL) {
perror("malloc fail");
return;
}
//将 待排序的数组、归并过程用的tmp临时数组、归并范围 传过去
_MergeSort(a, tmp, 0, n - 1); //因为 主函数中有malloc tmp的操作,若递归调用主函数,则每次调用都会malloc,再free 是对空间上的浪费
//因此用子函数进行递归 【_子函数】
free(tmp);
}
(4)归并排序效率分析
1)时间复杂度 O(N*logN)
二分 有 logN 层 ,也正是因为是logN层,递归深度不会太深,所以不用考虑非递归,当然非递归也能实现。
每层有N个数进行归并排序
=>N*logN
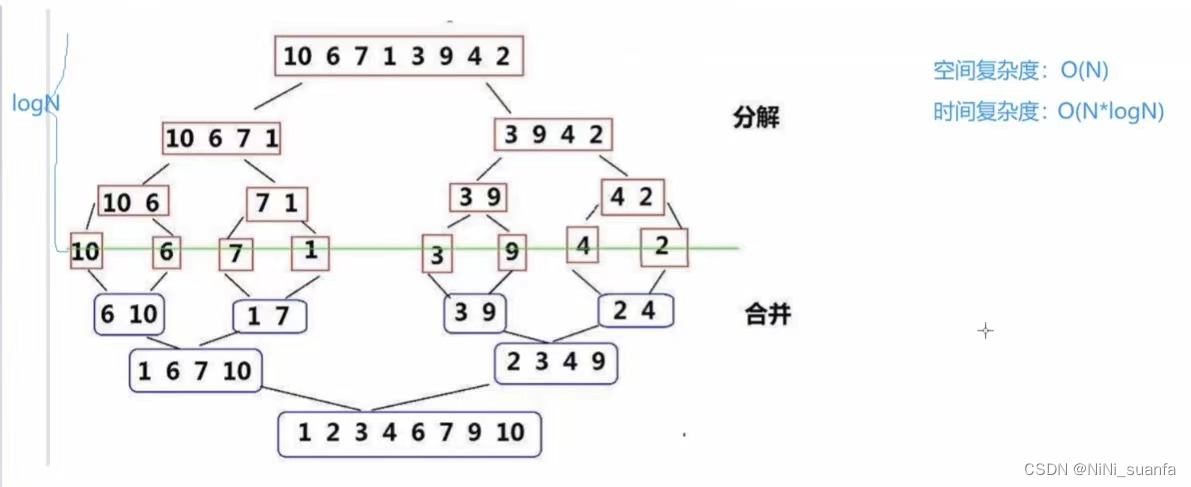
2)空间复杂度 O(N)
开辟了个 空间大小为N的 新的数组,用于归并有序的过程。
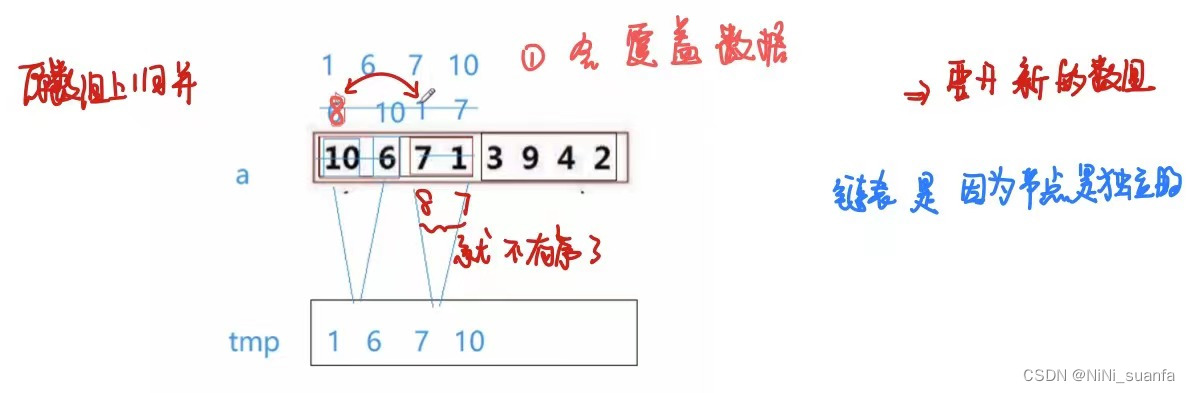
在原数组上归并会出现什么问题:
- 会覆盖数据
- 最小的1换到8的位置后,8和7就不再保持有序了。
稳定性:稳定
二、归并排序的非递归实现
归并排序是 二分的思想 => logN层 => 递归不会太深、且现编译器优化后,递归、非递归的性能差距没有那么大了 =>所以不用考虑非递归,但非递归实现也不难。下面带大家简单实现一下。
(1) 关于递归的缺点的讨论
递归的缺点:递归消耗栈帧,递归的层数太深,容易爆栈。
【栈的空间比较小,在x86(32位)环境下,只有8M。(对比同一环境下的堆,则有2G+)。因为平时函数调用开不了多少个栈帧。理论上递归深度>1w 可能就会爆 ,但实际上5k左右就爆掉了】
这时就需要改非递归了
★递归—>非递归:
- 改循环
- 利用 [ 数据结构 ] 栈(本质上是通过malloc 在堆上开辟的内存空间,内存空间足够大)
- 递归逆着来求(如斐波那契数列逆着来求也是可行的)【归并排序的非递归实现 也是个很好的例子】
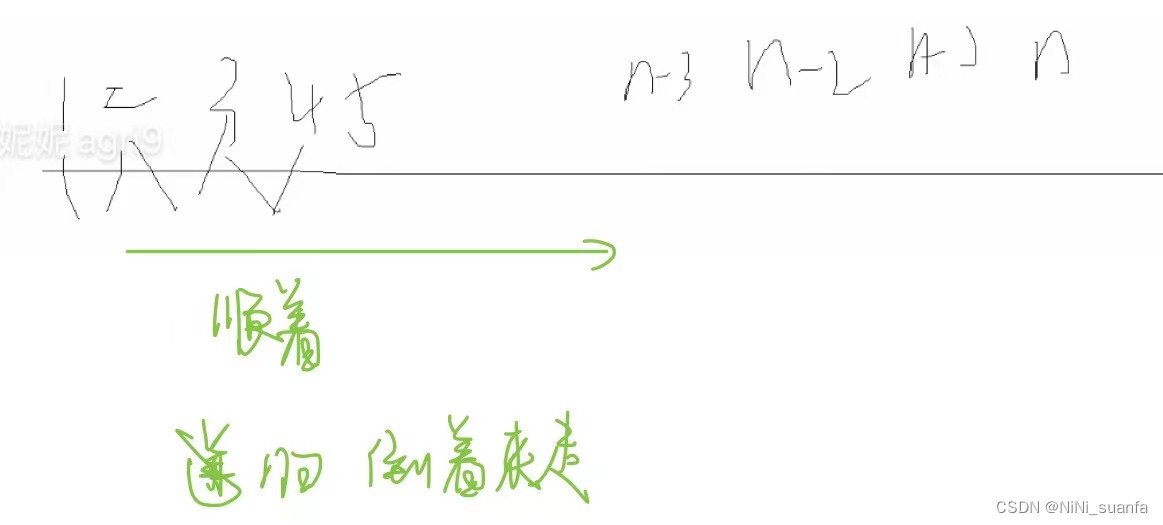 而归并排序的非递归实现则是用到了其中的第三点 。
而归并排序的非递归实现则是用到了其中的第三点 。
(2) 归并排序 非递归算法实现思路
虽说不是递归,是递归的逆序版。是直接从最深层次,逆序回去,直接开始归并排序,免去了向下深入递归。虽说不是递归,但也算是递归的思路的另一个种实现。

- 开辟新的数组(临时存放)用于归并排序过程
- int gap=1;gap*=2【gap控制归并的范围:11归并,22归并,44归并】
- for (int i = 0; i < n; i += 2 * gap) { 【i 控制进行比较轮到的组号,控制进行归并的组号】
- 归并完一轮,将归并好的有序数组拷贝回原数组memcpy 。
- 进入新的一轮归并,直至gap>n则归并完成
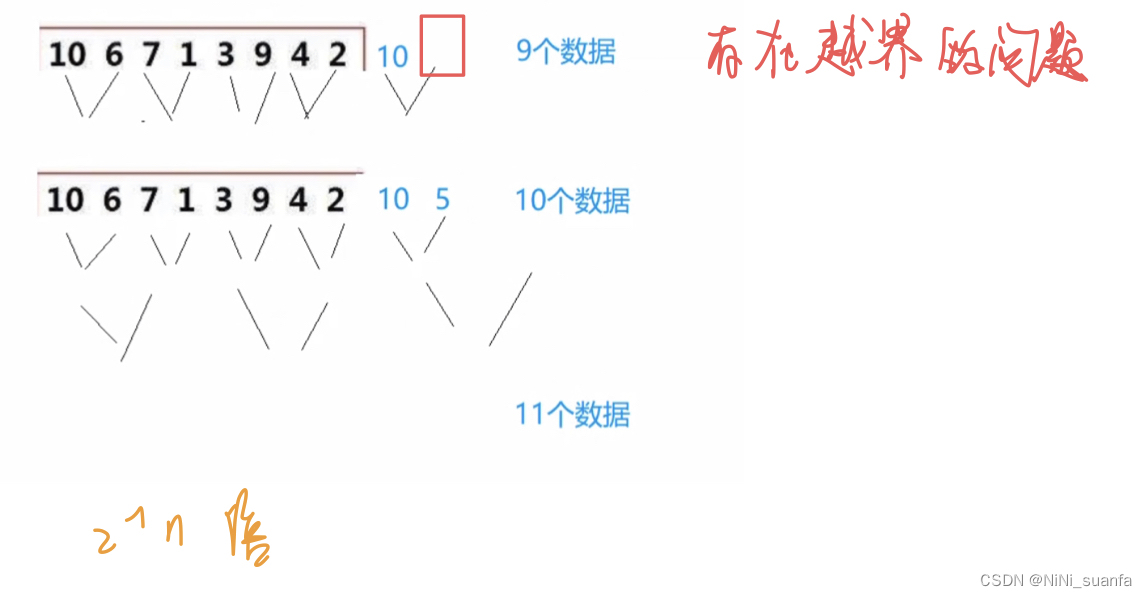
☆注意的两个情况
6. if (begin2 >= n) { break; } 第二组不存在,这一组不用归并了
7. if (end2 > n) { end2 = n - 1; } 第二组右边界越界问题,修正一下
(3)码源详解
//归并排序——非递归版 :从最底层开始,逆着往回求(如同斐波那契)
void MergeSortNonR(DataType* a,int n) {
DataType* tmp = (DataType*)malloc(sizeof(DataType) * n); //开辟新的数组(临时存放)用于归并排序过程
if (tmp == NULL) {
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n) { //gap控制 11归并,22归并,44归并
//i控制进行比较轮到的组号,控制归并的组号
for (int i = 0; i < n; i += 2 * gap) { //可以通过画出数组,在草稿纸上演示,理清要比较的数begin1、end1、begin2、end2之间和i、gap的数量关系
//[begin1,end1][begin2,end2]归并
int begin1 = i; int end1 = i + gap - 1; //-1 控制下标的边界
int begin2 = i + gap; int end2 = i + 2 * gap - 1;
//如果第二组不存在,这一组不用归并了
if (begin2 >= n) {
break;
}
//第二组右边界越界问题,修正一下
if (end2 > n) {
end2 = n - 1;
}
int index = i;
while (begin1 <= end1 && begin2 <= end2) { //&& 其中一组不满足了条件了(其中一个数组遍历完了)就不再继续,就跳出循环
if (a[begin1] < a[begin2]) { //两个数组比对,小的放进去
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1) { //把剩下的没遍历进去的数组剩余的部分 遍历进去
tmp[index++] = a[begin1++];
}
while (begin2 <= end2) {
tmp[index++] = a[begin2++];
}
//拷贝回原数组
//通过a+i、tmp+i来找到要拷贝数组部分的对应下标
memcpy(a + i, tmp + i,(end2-i+1)*sizeof(DataType));
}
printf("\n");
gap *= 2; //gap控制总体归并
}
free(tmp);
}
(4)运行结果
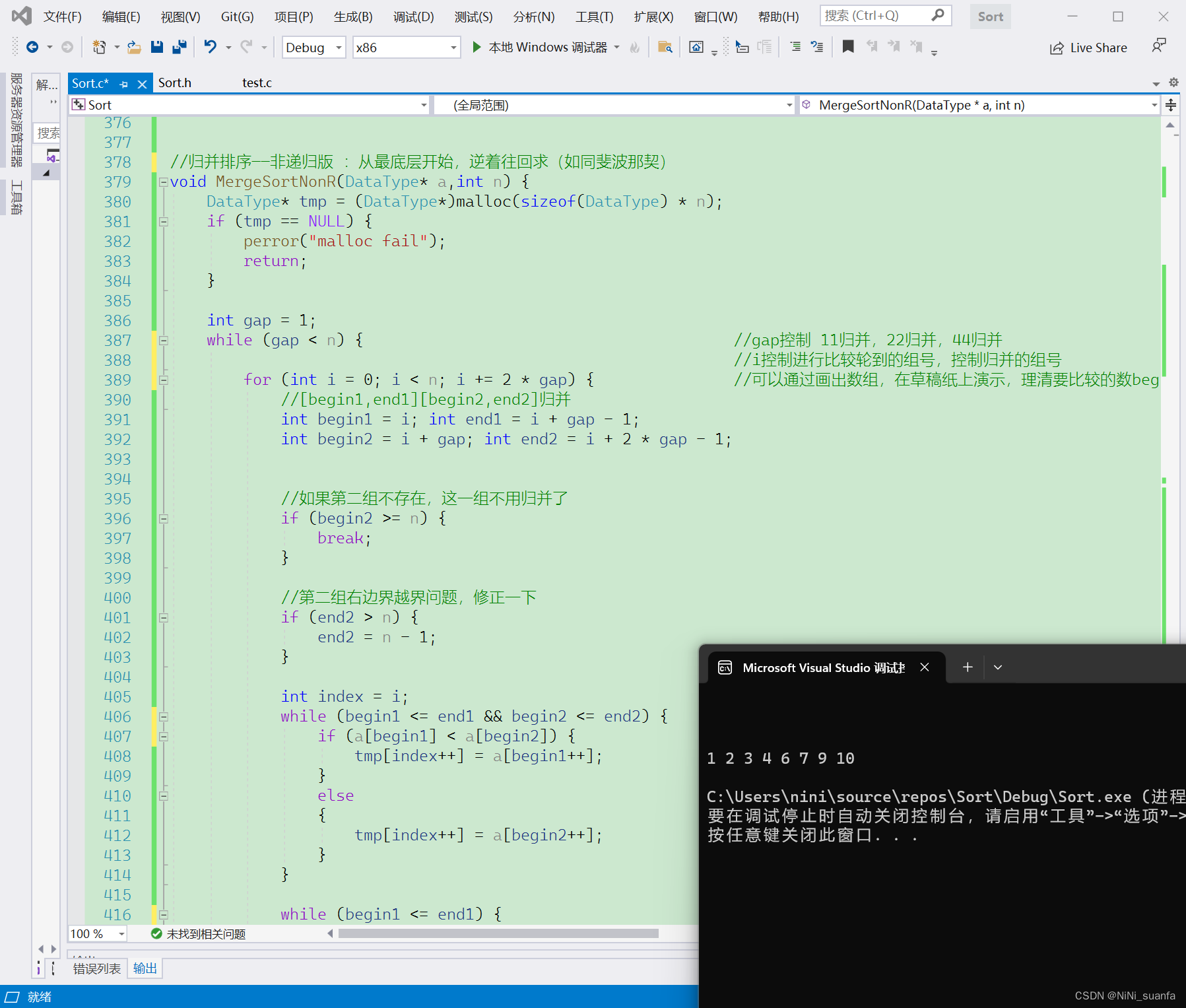
![[AUTOSAR][诊断管理][ECU][$85] 设置DTC功能](https://img-blog.csdnimg.cn/6bf34e200a2e400881c9ffaab2d3353b.png)


![[概述] 点云滤波器](https://img-blog.csdnimg.cn/68d8c556e3754a709bf28b13be560c45.png)