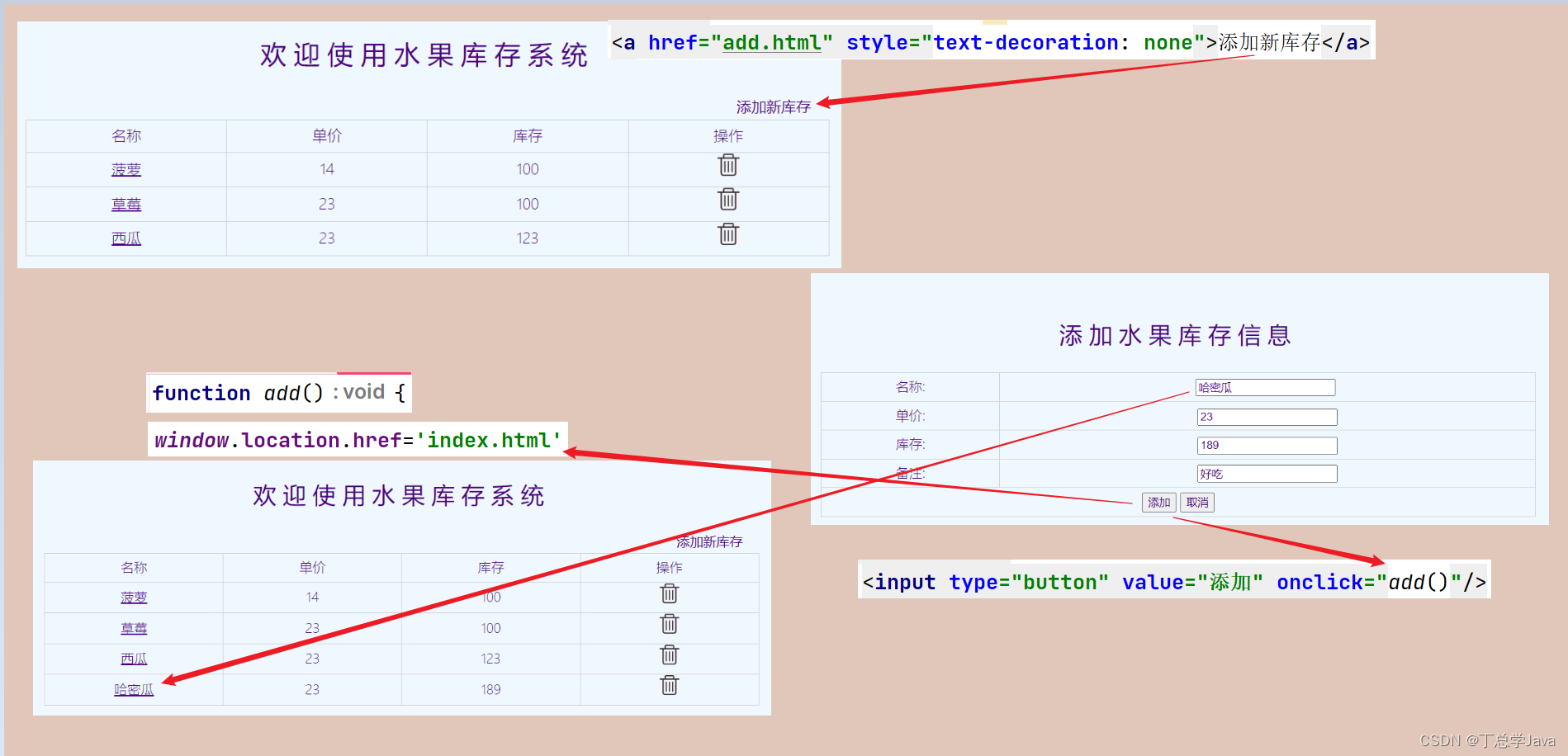
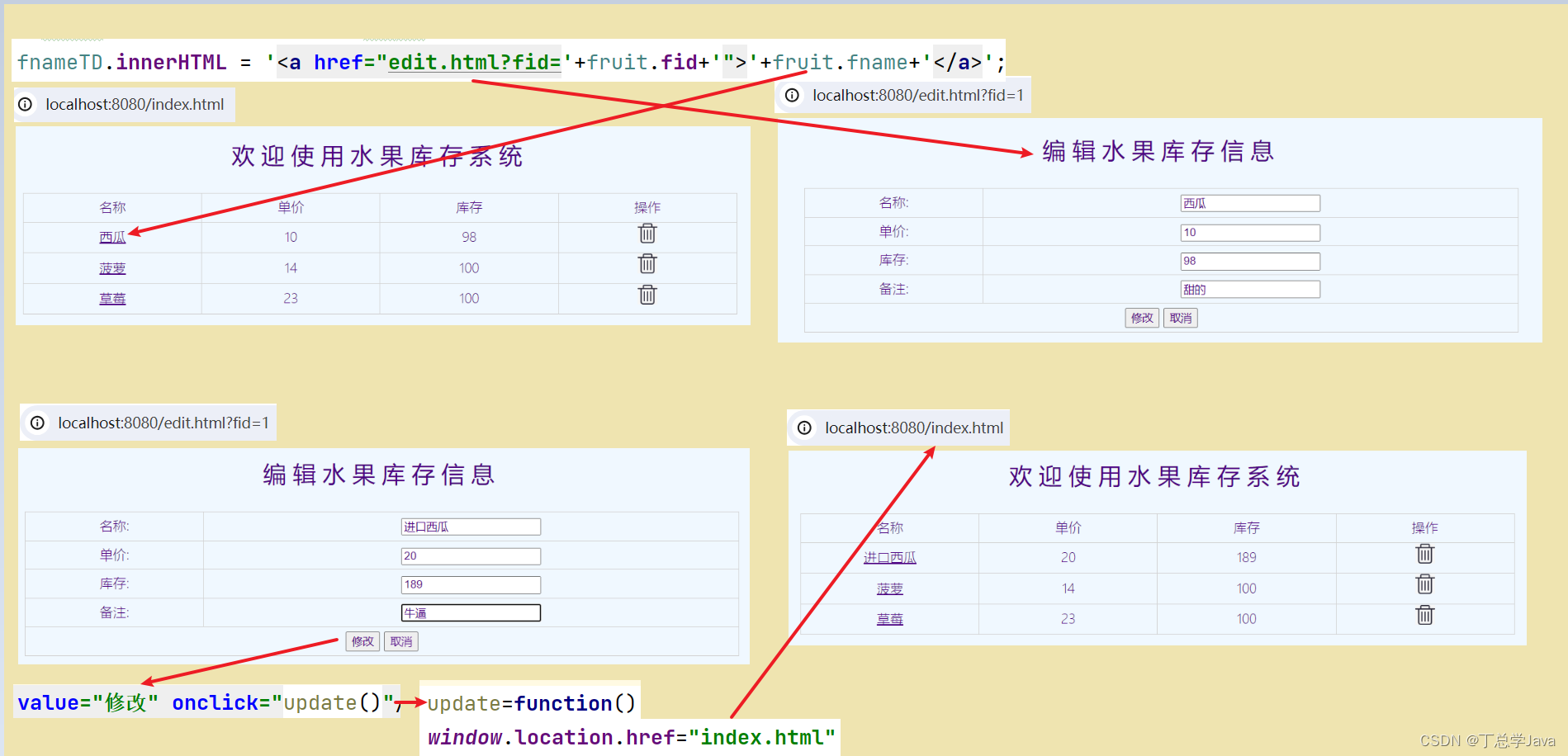
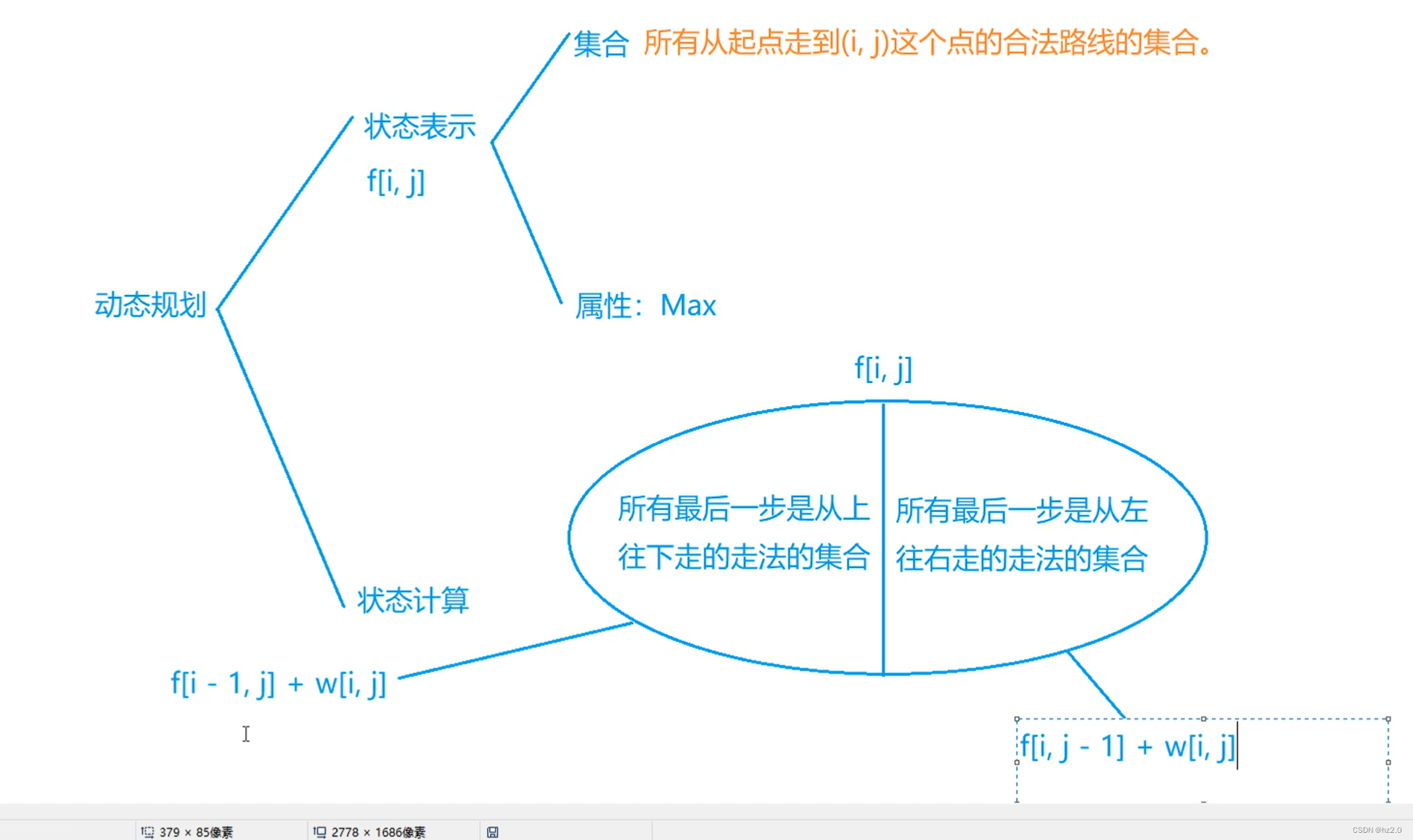
1.二叉树的性质

1.在二叉树的第 i 层上至多有 2^(i-1) 个结点。

2.深度为 k 的二叉树至多有 2^k - 1 个结点。

3.对于任意一棵二叉树，如果叶节点数为 N0 ，度数为 2 的结点总数为 N2 ，则 N0=N2+1 。

4.具有 n 个结点的完全二叉树的深度为 log2(n+1) 。

5.对于完全二叉树，从上至下，从左至右编号，编号为 i 的结点，左孩子编号必为 2i ，右孩子编号必为 2i+1 ，双亲编号必为 i/2 （ i=1 时除外）。

2.定义二叉树

定义二叉树：

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
}

定义N叉树：

public class TreeNode {
    int val;
    List<TreeNode> nodes;
}

3.树的遍历

树的遍历分为深度优先遍历和广度优先遍历。
广度优先遍历也叫层次遍历。
深度优先遍历分为先序遍历，中序遍历，后序遍历。

4.通过序列构造二叉树

给定三个序列：

先序：1 2 3 4 5 6 8 7 9 10 11 12 13 15 14
中序：3 4 8 6 7 5 2 1 10 9 11 15 13 14 12
后序：8 7 6 5 4 3 2 10 15 14 13 12 11 9 1

4.1 前中序列构造二叉树

根据先序确定根节点，然后根据中序将左子树和右子树分开。

第一轮：

第二轮：

第三轮：

重复步骤，最终结果为：

4.2 中后序列构造二叉树

后序序列的最后一个是根节点，根据根节点在中序序列中将左子树和右子树区分开。

流程的图示和上面的相同。

4.3 关于前后序列无法构造二叉树的思考

前后序列都可以获得根节点，但是无法知道中间元素是如何被区分开的，所以不能构造二叉树。

4.4 前序和中序构造树的算法题

【持续更新】

4.5 中序和后序构造树的算法题

【持续更新】

如果对您有帮助，请点赞关注支持我，谢谢！❤
如有错误或者不足之处，敬请指正！❤
个人主页：星不易 ❤
算法通关村专栏：不易|算法通关村 ❤