2015年亚太杯APMCM数学建模大赛
C题 识别网络中的错误连接
原题再现
网络是描述真实系统结构的强大工具——社交网络描述人与人之间的关系,万维网描述网页之间的超链接关系。随着现代技术的发展,我们积累了越来越多的网络数据,但这些数据部分不完整、不准确,有时甚至失真。例如,在生物网络中,一些早期证明的现有基因-基因和蛋白质-蛋白质相互关系被更高精度的新实验推翻。
本主题将用6个网络的数据来解决生物学、信息和社交网络中的真实网络问题。这些网络的规模从数百个节点到数百万个节点不等。每个网络连接可能是无定向的(例如,推特中的朋友连接),也可能是定向的(如人们在推特中“关注”他人)。在原始真实网络的基础上,我们添加了一些符合以下标准的假连接:(1)假连接的数量不超过连接总数的10%;(2) 错误连接是以完全随机的方式选取的。
请阅读附录中的信息,并解决以下问题:
(1) 开发一个数学模型来理解网络的结构和组织机制。不同类型网络的结构特征和组织原则并不总是相同的。
(2) 提出了一种识别错误连接的有效方法。显示如何发现结构特征的完整性;说明了数学模型的有效性和准确性以及算法的准确性。
附件
数据描述
与该问题相关的网络在表1中编号为1至6。补充信息中给出了数据本身及其如何获得数据的详细描述。
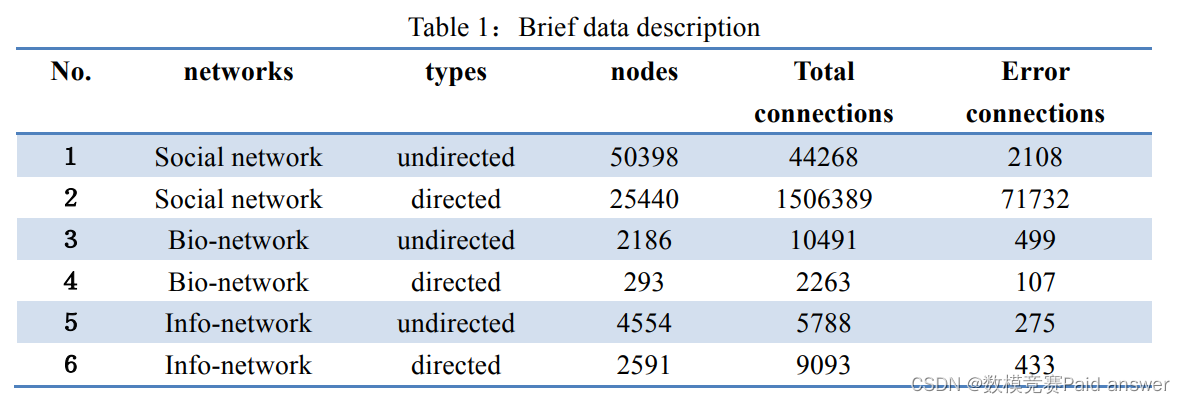
对于上述网络中的任何一个,如果错误连接的真实数量是R,则玩家应提交如何以标准格式识别这些R个错误连接(请参阅补充信息以了解提交的标准格式)。如果r个错误连接中的r个在提交中被正确识别,则得分为r/r。玩家在所有6个网络中获得的总分是衡量算法准确性的唯一指标。
整体求解过程概述(摘要)
本文分析了复杂网络的结构性质,研究了六种网络中错误连接的识别问题。对于这些网络,我们考虑了它们的拓扑结构,并进一步分析了一些特定的特性。
首先,我们通过绘制网络的视觉图形来对它们进行视觉研究。经过分析,我们发现几乎所有的网络都存在小世界效应、大分支及其程度分布向右倾斜。生物定向网络不服从幂律,其社会分化明显。生物无向网络和有向网络除了服从幂律和具有协调性外,几乎是一样的。信息网络的节点不具有模块性,并且非常分散。两个网络都服从幂律和非关联性。对于社交网络,定向网络服从幂律。无向网络与有向网络几乎相同。然而,它并没有巨大的分支。
其次,我们发现生物定向网络与食物链具有相似的特征,生物无定向网络与生物器官相似。对于这两种网络,我们都使用入度和出度以及公共邻居相似性来识别错误连接。结果表明,生物定向网络的精度为0.364,无定向网络的准确度为0.226。信息导向网络类似于互联网。我们使用了入度、出度和PageRank的排序来获得错误连接。两个信息网络具有相同的特性。结果表明,信息定向网络的精度为0.173,无定向网络的准确度为0.309。对于社交导向网络,我们认为它和推特有密切的关注模式。因此,我们假设“大V”节点和“活跃用户”节点的存在。通过对其拓扑算法的分析,我们最终得出准确率为0.679的结果。对于社交无向网络,我们认为它与twitter的好友添加模式具有相同的模式。我们使用相同的方法来处理它,最终结果是0.338。
模型假设:
1.该错误不会影响每个网络的真实链路拓扑特性。
2.每个网络的特异性都很低,大多数节点都遵循一定的规律性。
问题分析:
本研究是现代社会的一个问题,随着网络的积累越来越多,我们如何应对日益庞大复杂的网络数据分析。
一个问题需要我们对不同的网络体系结构模型分别进行分析,分析其结构和内部机制。首先,我们对数据进行分析,得出不同的网络,如度分布、聚类系数、每个顶点的连接平均测地线距离等。利用这些数据,我们可以分析网络的基本性质。然后我们利用这些数据,建立了每个网络的随机图模型,通过分析和比较模型与原始网络,了解每个网络的不同结构。
第二个问题要求我们提出一种有效的方法来识别六种不同网络连接中的错误,并展示完整的结构特征,从中发现和解释数学模型和算法的有效性和准确性。通过第一个问题我们已经知道了这些网络拓扑的结构性质,网络分别是有机体、生物无向网络、信息有向网络、无向网络,社交网络有别于社交网络本身的无向结构特征的背离,做出了合理的分析,其中一些肯定会去除正确的链接,然后应用基于相似度的链接预测方法,建立共同的邻居相似度指数,找出错误的链接。
模型的建立与求解整体论文缩略图


全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:
部分程序如下:
clear;clc;close
A=load('InfoUD.mat');
P=100;
B=[];
B(:,1)=A.node1;
B(:,2)=A.node2;
if ~all(all(B(:,1:2)));
B(:,1:2)=B(:,1:2)+1;
end
num=max(max(B));
C=zeros(num);
n=length(B);
for i=1:n
C(B(i,1),B(i,2))=C(B(i,1),B(i,2))+1;
end
C=C+C';
R=get_degree_correlation(C);
[M,N_DeD,N_predict,DeD,aver_DeD]=Degree_Distribution(C,P);
N_predict=floor(N_predict);
j=sum(N_predict);
D=[];
for k=1:P+1
D=[D (k-1)*ones(1,N_predict(k))];
end
function [ out ] = get_degree(A,k)
row = A(k,:);
out=size(find(row==1),2);
end
function [M,N_DeD,N_predict,DeD,aver_DeD]=Degree_Distribution(A,P)
N=size(A,2);
DeD=zeros(1,N);
for i=1:N
DeD(i)=sum(A(i,:));
end
aver_DeD=mean(DeD);
if sum(DeD)==0
disp(' 该网络只是由一些孤立点组成');
return;
else
figure;
bar([1:N],DeD);
xlabel('节点编号n');
ylabel('¸各节点度数K');
title('网络中各节点度数大小K的分布图');
end
figure;
M=max(DeD);
predict=0:P;
for i=1:M+1;
N_DeD(i)=length(find(DeD==i-1));
end
P_DeD=zeros(1,M+1);
P_DeD(:)=N_DeD(:);
bar([0:M],P_DeD,'r');
xlabel('节点的度K');
ylabel('度为K的节点个数');
title('网络中的节点度个数分布图 ');
hold on
N_predict=interp1([0:M],N_DeD,predict,'spline');
plot(predict,N_predict);
hold off
figure;
PK_DeD=zeros(1,M+1);
PK_DeD(:)=N_DeD(:)./sum(N_DeD);
bar([0:M],PK_DeD);
set(gca,'yscale','log','xscale','log');
xlabel('度k');
ylabel('度为k的顶点所占比例');
title('幂律度分布')
function [ r ] = get_degree_correlation( A)
B = triu(A);
M = size(find(B==1),1);
sum1=0;
sum2=0;
sum3=0;
A1 = find(B==1);
length = size(A1,1);
for i=1:length
[x y]=ind2sub(size(B),A1(i));
sum1 = sum1+get_degree(A,x)*get_degree(A,y);
sum2 = sum2+get_degree(A,x)+get_degree(A,y);
sum3 = sum3+get_degree(A,x)^2+get_degree(A,y)^2;
end
x1 = sum1/M-(sum2/(2*M))^2;
y1 = sum3/(2*M)-(sum2/(2*M))^2;
r=x1/y1;
end
clear;clc;close
A=load('InfoUD.mat');
P=100;
B=[];
B(:,1)=[A.node1;A.node2];
B(:,2)=[A.node2;A.node1];
load('InfoUD_DeD.mat')
B1=B(:,1);
num0=unique(B1);
mini=min(num0);
maxi=max(num0);
check=mini:maxi;
len=length(check);
i=1;
leak_num=0;
leak=NaN*ones(len);
while i == len
if num0(i)==check(i)
i=i+1;
else
que_num=num0(i)-check(i);
std_num=leak_num;
final_num=que_num+leak_num;
leak(std_num+1:final_num)=i:i+que_num-1;
i=i+que_num;
end
end
B2=B(:,2);
index=1:len;
reform_data=NaN*ones(len,len);
leak_std=1;
for j=index
if j==leak(leak_std)
leak_std=leak_std+1;
continue;
else
judge_sign = (B1 == check(j));
term=sum(judge_sign);
reform_data(1:term,j)=B2(judge_sign);
end
end
L=zeros(len);
S_xy=zeros(len);
AV_DeD=zeros(len);
for i=index
for j=index
Lx=reform_data(:,i);
Ly=reform_data(:,j);
Lx=Lx(~isnan(Lx));
Ly=Ly(~isnan(Ly));
L(i,j)=length((intersect(Lx,Ly)));
AV_DeD(i,j)=DeD(i)+DeD(j);
S_xy(i,j)=2*L(i,j)/(DeD(i)+DeD(j));
end
end
clear;clc;
A=load('S_xy_BU.mat');
UA=load('BioD.mat');
UVA=load('AV_DeD_BioUD.mat');
len1=length(UA.node1);
%C=load('C.mat');
C=zeros(len1,4);
%len1=length(C.C);
D=zeros(len1,4);
C(:,1)=UA.node1;
C(:,2)=UA.node2;
len=length(A.S_xy);
index=1:len;
B=zeros(sum(index),4);
i=1;
k=1;
while i<len+1
B(k:k+len-i,1)=i*ones(len+1-i,1);
B(k:k+len-i,2)=i:len;
B(k:k+len-i,3)=A.S_xy(i,i:len);
B(k:k+len-i,4)=UVA.AV_DeD(i,i:len);
k=k+1+len-i;
i=i+1;
end
B(:,1:2)=B(:,1:2)-1;
[B1 B2]=find(isnan(B));
B(B1,:)=[];
len2=length(B);