日期:11.2 星期三
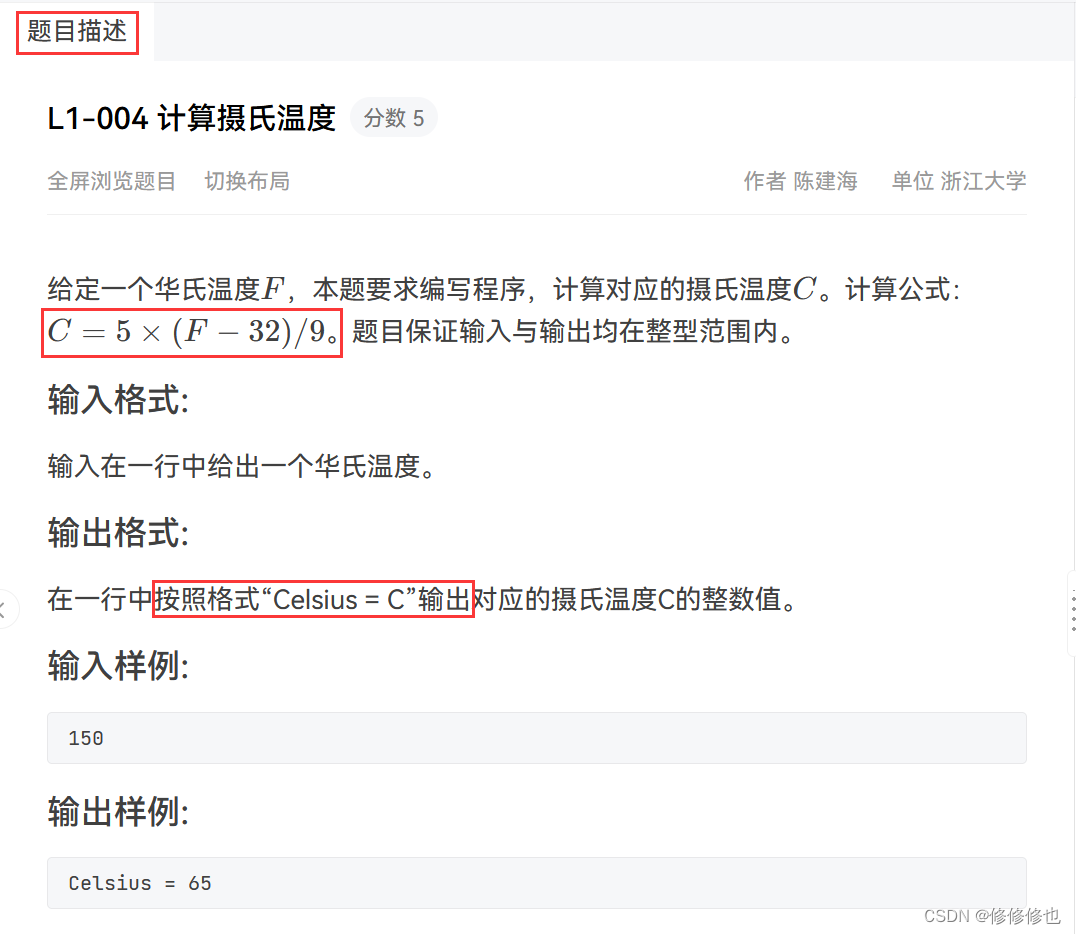
L1-004 计算摄氏温度
题目描述
给定一个华氏温度F,本题要求编写程序,计算对应的摄氏温度C。计算公式:C=5×(F−32)/9。题目保证输入与输出均在整型范围内。
输入描述
输入在一行中给出一个华氏温度。
输出描述
在一行中按照格式“Celsius = C”输出对应的摄氏温度C的整数值。
输入样例
150
输出样例
Celsius = 65
解题代码
int main()
{
int f=0;
scanf("%d",&f);
int c=5*(f-32)/9;//照题中给出的公式进行计算
printf("Celsius = %d",c);//输出也按照输出案例输出即可
return 0;
}本题的解题步骤为:
- 接收系统输入值
- 使用公式计算
- 输出计算结果
细节详解见代码注释.
提交结果

L1-005 考试座位号
题目描述
每个 PAT 考生在参加考试时都会被分配两个座位号,一个是试机座位,一个是考试座位。正常情况下,考生在入场时先得到试机座位号码,入座进入试机状态后,系统会显示该考生的考试座位号码,考试时考生需要换到考试座位就座。但有些考生迟到了,试机已经结束,他们只能拿着领到的试机座位号码求助于你,从后台查出他们的考试座位号码。
输入描述
输入第一行给出一个正整数 N(≤1000),随后 N 行,每行给出一个考生的信息:
准考证号 试机座位号 考试座位号。其中准考证号由 16 位数字组成,座位从 1 到 N 编号。输入保证每个人的准考证号都不同,并且任何时候都不会把两个人分配到同一个座位上。考生信息之后,给出一个正整数 M(≤N),随后一行中给出 M 个待查询的试机座位号码,以空格分隔。
输出描述
对应每个需要查询的试机座位号码,在一行中输出对应考生的准考证号和考试座位号码,中间用 1 个空格分隔。
输入样例
4
3310120150912233 2 4
3310120150912119 4 1
3310120150912126 1 3
3310120150912002 3 2
2
3 4
输出样例
3310120150912002 2
3310120150912119 1


解题代码
#include<stdio.h>
#include<stdio.h>
typedef struct stu
{
char idea[17];//留一位存'\0'!
int s; //存放试机座位号码信息
int k; //存放考试座位号码信息
}stu;
int main()
{
int n = 0;
scanf("%d", &n);
stu data[n];//创建结构体数组存放所有人的考号,座位号,考试号等信息
int i = 0;
while (i < n)
{
scanf("%s", data[i].idea);//接收考生考号,放在结构体数组中
scanf("%d", &data[i].s);//接收试机号
scanf("%d", &data[i].k);//接收考试座位号
i++;
}
int c = 0;
scanf("%d", &c);//接收要查询的考生的个数
i = 0;
while (i < c)//依据考生个数循环查询次数
{
int s = 0, j = 0;//用s接收试机号,与结构体成员s进行比对
//用j遍历结构体数组
scanf("%d", &s);
while (j < n)
{
if (s == data[j].s)//如果两个s相等,说明找到了
{
printf("%s %d\n", data[j].idea, data[j].k);
//找到了之后打印考生的学号和考试位置信息即可
break;//打印完跳出循环
}
j++;//没找到就继续向后找
}
i++;//完成了一个考生的查,下面循环下一个考生的查
}
}本题的解题步骤为:
- 创建结构体数组存放考生信息
- 录入考生信息
- 遍历查询考生信息
- 找到信息后输出
细节详解见代码注释.
提交结果

L1-006 连续因子*
题目描述
一个正整数 N 的因子中可能存在若干连续的数字。例如 630 可以分解为 3×5×6×7,其中 5、6、7 就是 3 个连续的数字。给定任一正整数 N,要求编写程序求出最长连续因子的个数,并输出最小的连续因子序列。
输入描述
输入在一行中给出一个正整数 N(1<N<231)。
输出描述
首先在第 1 行输出最长连续因子的个数;然后在第 2 行中按
因子1*因子2*……*因子k的格式输出最小的连续因子序列,其中因子按递增顺序输出,1 不算在内。
输入样例
630
输出样例
3
5*6*7

解题代码
#include <stdio.h>
int main()
{
unsigned int N;
scanf("%u", &N); // 输入正整数 N
unsigned int maxLength = 0; // 最长连续因子的个数
unsigned int start = 0; // 最小连续因子序列的起始因子
// 枚举因子 i,i 的最大取值为 sqrt(N)
for (unsigned int i = 2; i * i <= N; i++)
{
unsigned int j = i; // j 从 i 开始
unsigned int product = 1; // 初始化连续因子的乘积为 1
// 枚举连续因子 j,直到乘积不再是 N 的因子
while (1)
{
product *= j;
if (N % product != 0) // 如果乘积不再是 N 的因子,则退出循环
break;
// 如果当前连续因子个数大于之前的记录,则更新最长连续因子的个数和最小连续因子序列的起始因子
if (j - i + 1 > maxLength)
{
maxLength = j - i + 1;
start = i;
}
j++; // j 自增
}
}
// 如果最长连续因子的个数为 0,则 N 本身就是最小连续因子序列
if (maxLength == 0) {
printf("1\n%u\n", N);
} else {
printf("%u\n", maxLength);
// 输出最小连续因子序列
for (unsigned int i = 0; i < maxLength; i++) {
printf("%u", start + i);
if (i != maxLength - 1)
printf("*");
}
printf("\n");
}
return 0;
}
本题的解题步骤为:
- 首先,我们需要枚举因子 i,i 的最大取值为 sqrt(N)。因为如果 N 有一个大于 sqrt(N) 的因子,那么另一个因子就会小于 sqrt(N),这样的两个因子是不连续的。
- 对于每个因子 i,我们从 i 开始枚举连续因子 j,直到乘积不再是 N 的因子。在这个过程中,我们不断更新最长连续因子的个数和最小连续因子序列的起始因子。
- 如果最长连续因子的个数为 0,说明 N 本身就是最小连续因子序列。
- 如果最长连续因子的个数不为 0,我们输出最小连续因子序列。
- 这样,我们就可以找到最长连续因子的个数,并输出最小的连续因子序列。
细节详解见代码注释.
提交结果