看了不少解读和笔记,本文把最容易理解的解读做个总结。
1. 蒙特卡洛方法
蒙特卡洛方法(Monte Carlo method),是一种“统计模拟方法”。20世纪40年代,为建造核武器,冯.诺伊曼 等人发明了该算法。因赌城蒙特卡洛而得名,暗示其以概率作为算法的基础。
假设我们要计算一个不规则形状的面积,我们只需在包含这个不规则形状的矩形内,随机的掷出一个点,每掷出一个点,则N+1,如果这个点在不规则图形内则W+1。落入不规则图形的概率即为 W/N。当掷出足够多的点之后,我们可以认为:不规则图形面积=矩形面积*W/N。
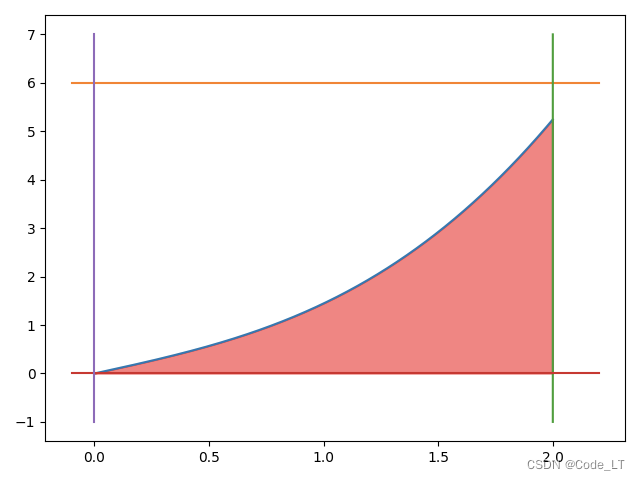
例如:计算如下红色图形的面积:
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import math
def func(x):
a = 0.1 * x ** 1.0/3
b = np.sin(x / math.pi)
y = a + (b + 0.1 * x) * x ** 2 + x
return y
def integral():
n = 20000000
x_min, x_max = 0, 2.0
y_min, y_max = 0, 6.0
# count = 0, 随机抛点
x = np.random.uniform(x_min, x_max, size=(n, 1))
y = np.random.uniform(y_min, y_max, size=(n, 1))
yy = func(x)
c = np.sum(yy > y)
ratio = c / float(n)
res = ratio * 2.0 * 6.0
print(res)
integral()
# 3.6831354000000003
2. 蒙特卡洛树搜索(Monte Carlo Tree Search,MCTS)算法
了解了上面 蒙特卡洛方法 不是MCTS就行,MCTS只是在一定程度上借用了上面的原理,看一百篇静态的文章都不如看一篇动态的视频(一定重点理解视频中的示例变化过程):
b站-AI如何下棋?直观了解蒙特卡洛树搜索MCTS!!!
2.1 几个重要笔记

重点:

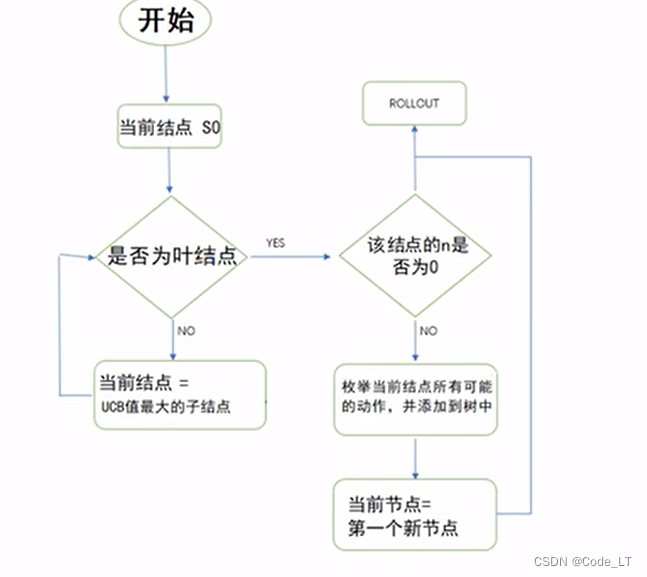

这里的终结指的是整个算法的终结,可以给出具体action了
simulation中(即rollout),如何确定terminal state以及terminal state的价值是另外一个话题(见下)。
2.2 几个注意点
如何确定terminal state以及terminal state的价值?
- 对于一般胜负类的游戏,可简单粗暴的用胜利或者失败作为游戏结局,胜利价值为1,失败价值为0
- 对于其他更复杂的场景,可以自行定义价值函数,比如用的步骤越多价值越低。
MCTS是如何利用蒙特卡洛方法思想的?
当重复的次数多了以后,每个节点的ucb值其实就代表了它价值的真实值(这个值是一个相对概念,相对于同层的其他节点,值越大,就代表越好),这样就能指导采用哪个节点行动了。
参考
蒙特卡洛树搜索最通俗入门指南
蒙特卡罗方法、蒙特卡洛树搜索(Monte Carlo Tree Search,MCTS)初探
【最佳实战】蒙特卡洛树搜索算法
面向初学者的蒙特卡洛树搜索MCTS详解及其实现
【详细原理】蒙特卡洛树搜索入门教程!
git-MCTS代码
b站-AI如何下棋?直观了解蒙特卡洛树搜索MCTS!!!
b站-【强化学习】规划与学习-蒙特卡洛树搜索 MCTS