损失函数(Loss Function)一文详解-聚类问题常见损失函数Python代码实现+计算原理解析

前言

损失函数无疑是机器学习和深度学习效果验证的核心检验功能，用于评估模型预测值与实际值之间的差异。我们学习机器学习和深度学习或多或少都接触到了损失函数，但是我们缺少细致的对损失函数进行分类，或者系统的学习损失函数在不同的算法和任务中的不同的应用。因此有必要对整个损失函数体系有个比较全面的认识，方便以后我们遇到各类功能不同的损失函数有个清楚的认知，而且一般面试以及论文写作基本都会对这方面的知识涉及的非常深入。故本篇文章将结合实际Python代码实现损失函数功能，以及对整个损失函数体系进行深入了解。

博主专注建模四年，参与过大大小小数十来次数学建模，理解各类模型原理以及每种模型的建模流程和各类题目分析方法。此专栏的目的就是为了让零基础快速使用各类数学模型、机器学习和深度学习以及代码，每一篇文章都包含实战项目以及可运行代码。博主紧跟各类数模比赛，每场数模竞赛博主都会将最新的思路和代码写进此专栏以及详细思路和完全代码。若你渴望突破数学建模的瓶颈，不要错过笔者精心打造的专栏。愿你能在这里找到你所需要的灵感与技巧，为你的建模之路添砖加瓦。
一文速学-数学建模常用模型

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

一、聚类问题损失函数概述

在聚类问题中，我们试图将数据集分成不同的组（簇），使得每个组内的数据点相似度较高，而不同组之间的相似度较低。聚类问题的目标是找到合适的簇划分，以最大程度地减小组内的差异，同时最大程度地增大组间的差异。在聚类问题中，并没有像监督学习中那样明确定义的损失函数，因为聚类问题通常是无监督学习，没有预先定义的目标变量。而聚类问题的损失函数通常用于度量簇划分的质量，并提供一种可优化的指标来衡量聚类结果的好坏。一般来说聚类问题的损失函数承担的功能有三种：

度量簇内相似度： 损失函数度量了每个簇内数据点的相似度，即簇内数据点之间的相似程度。通常情况下，簇内相似度越高，表示簇内的数据点越相似。
度量簇间差异： 损失函数也可以度量不同簇之间的差异，即不同簇之间的相似度。簇间差异越大，表示不同簇之间的数据点越不相似。
提供优化目标： 损失函数为聚类算法提供了一个可优化的目标。聚类算法的目标是通过最小化或最大化损失函数来寻找最佳的簇划分。

那么作为度量差距的算法，都有损失函数的通性，辅助我们建立的模型好坏与否，其效果有以下四条：

帮助确定最佳簇数： 通过调整簇数，可以观察损失函数的变化，从而帮助确定最佳的簇数。
评估聚类结果： 损失函数可以用于评估聚类算法的结果，帮助判断聚类是否合理，簇内的相似度是否高，簇间的差异是否明显。
指导优化过程： 在迭代优化过程中，聚类算法可以根据损失函数的值来调整簇划分，从而提升聚类的效果。
衡量聚类的稳定性： 损失函数可以用于衡量聚类结果的稳定性，即不同运行下的聚类结果是否一致。

总的来说，聚类问题的损失函数在聚类过程中起到了指导和评估的作用，帮助算法找到合适的簇划分，从而达到最佳的聚类效果。选择合适的损失函数可以根据具体问题的需求和数据的特点来进行，以获得满意的聚类结果。

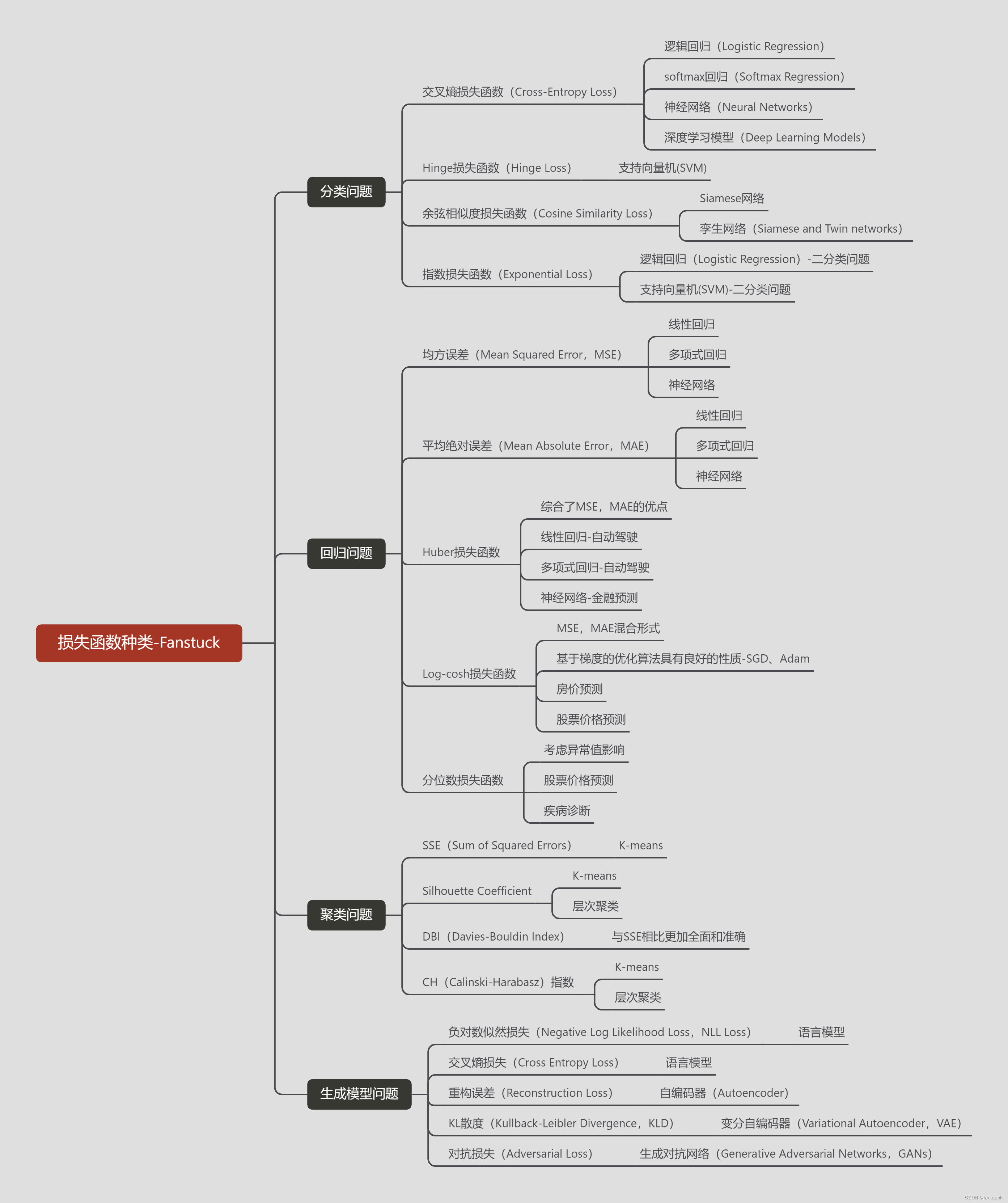
二、聚类函数种类

在这里插入图片描述

1.SSE（Sum of Squared Errors）

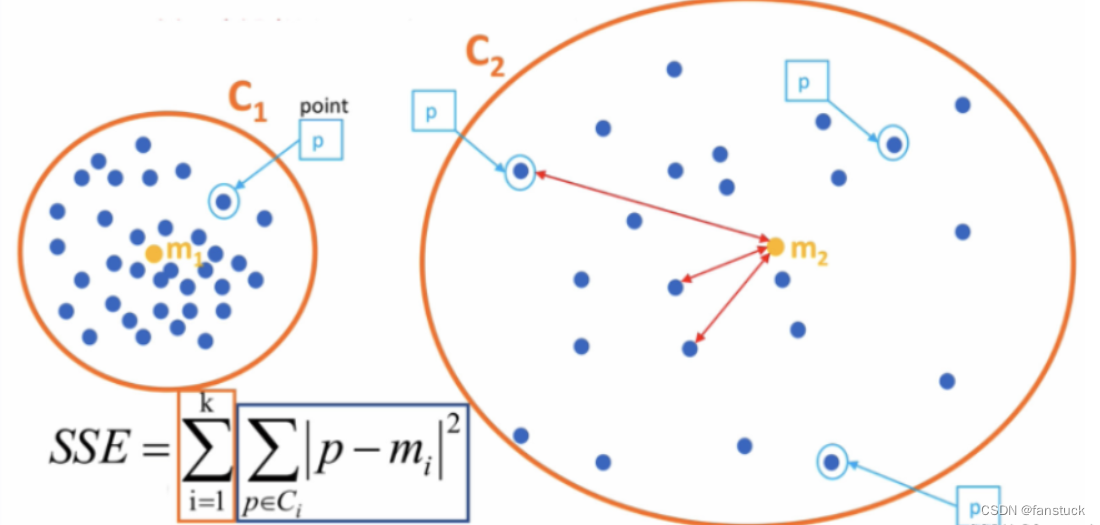
SSE（Sum of Squared Errors）是一种常用于聚类算法中的损失函数，也称为误差平方和。它衡量了每个数据点与其所属簇的质心之间的欧氏距离的平方的总和。

具体来说，对于一个包含 n 个数据点和 k 个簇的聚类结果，SSE 的计算公式如下：
$SSE=∑^n_{i=1}∑^k_{j=1}d(x_i,c_j)^2$
其中：

$x_{i}$ 表示第 i 个数据点。
$c_j$ 表示第 j 个簇的质心。
$d(x_{i},c_{j})$ 表示数据点 $x_{i}$ 与簇质心 $c_{j}$ 之间的欧氏距离。

SSE 的目标是最小化这个值，即通过调整簇的划分和质心的位置来使每个数据点与其所属簇的质心之间的距离尽可能小，从而达到聚类的效果。

SSE 的优点是简单直观，容易理解。然而，它也有一些缺点，例如它假设簇的形状是凸的，并且对异常值敏感。

在K均值聚类（K-Means）算法中，SSE 是一个重要的评估指标，通常用于确定最佳的簇数（K值）。通过尝试不同的K值，可以绘制出SSE随K值变化的曲线（称为“肘部法则”），从而选择最优的K值。
在这里插入图片描述

import matplotlib.pyplot as plt
import numpy as np

def calculate_euclidean_distance(point, centroid):
    return np.sum((point - centroid) ** 2)

def calculate_sse(data, centroids, labels):
    sse = 0
    for i in range(len(data)):
        sse += calculate_euclidean_distance(data[i], centroids[labels[i]])
    return sse

# 示例数据
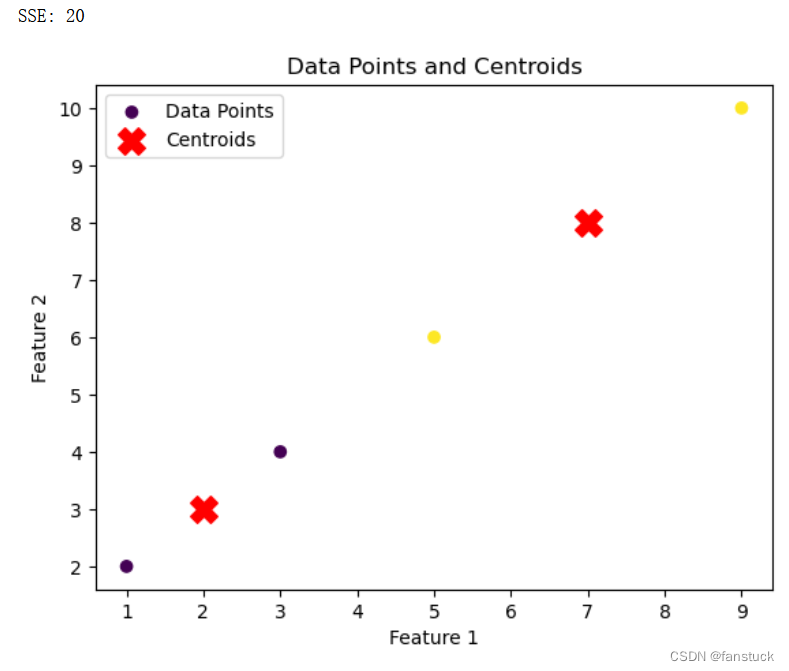
data = np.array([[1, 2], [3, 4], [5, 6], [7, 8], [9, 10]])
centroids = np.array([[2, 3], [7, 8]])
labels = np.array([0, 0, 1, 1, 1])  # 每个数据点所属的簇

sse = calculate_sse(data, centroids, labels)
print(f"SSE: {sse}")


# 绘制数据点
plt.scatter(data[:, 0], data[:, 1], c=labels, cmap='viridis', label='Data Points')
plt.scatter(centroids[:, 0], centroids[:, 1], marker='X', color='red', s=200, label='Centroids')

# 添加标题和标签
plt.title('Data Points and Centroids')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')

# 添加图例
plt.legend()

# 显示图形
plt.show()

2.Silhouette Coefficient

Silhouette Coefficient（轮廓系数）是一种用于评估聚类质量的指标，它同时考虑了簇内的紧密度和簇间的分离度。Silhouette Coefficient 的取值范围在 [-1, 1] 之间：

接近1表示样本被正确地分配到了簇中。
接近0表示样本位于簇的边界上。
接近-1表示样本被错误地分配到了相邻的簇中。

具体计算方法如下：

对于每个样本 $i$ ，计算以下两个值：

$a (i)$ 表示样本 $i$ 到同一簇中所有其他样本的平均距离（簇内平均距离）。
$b(i) $表示样本 $i$ 到最近簇中所有样本的平均距离（簇间平均距离）。

对于样本 $i$ ，Silhouette Coefficient 计算如下：
$s(i)=\frac{b(i)-a(i)}{max(a(i),b(i))}$
最终的 Silhouette Coefficient 是所有样本的 $s (i)$ 的均值。Silhouette Coefficient 的优点之一是它不需要事先知道聚类的数量，因此可以在不同的聚类数量下评估聚类的效果，帮助选择最优的聚类数量。需要注意的是，Silhouette Coefficient 对于凸形簇效果较好，但对于非凸形簇可能不太适用。Silhouette Coefficient 在其他聚类算法中的功能和作用如下：

衡量聚类效果： Silhouette Coefficient 提供了一种对聚类效果的定量评估。它能够指示聚类结果的紧密性和分离性，越接近1表示聚类效果越好。
选择最优聚类数量（K值）： Silhouette Coefficient 不需要事先知道聚类的数量，因此可以在不同的K值下评估聚类的效果，帮助选择最优的聚类数量。
辅助于数据可视化和解释： 在可视化和解释聚类结果时，Silhouette Coefficient 可以提供一个客观的评估指标，帮助理解聚类的效果。

在Python中，你可以使用scikit-learn库来计算Silhouette Coefficient。scikit-learn提供了一个名为silhouette_score的函数，可以方便地计算给定数据集和聚类结果的Silhouette Coefficient。

from sklearn.metrics import silhouette_score
from sklearn.cluster import KMeans
import numpy as np

# 假设 data, labels 已经定义

# 示例数据
data = np.array([[1, 2], [3, 4], [5, 6], [7, 8], [9, 10]])
labels = np.array([0, 0, 1, 1, 1])  # 每个数据点所属的簇

# 使用KMeans聚类算法进行聚类
kmeans = KMeans(n_clusters=2, random_state=0).fit(data)
labels = kmeans.labels_

# 计算Silhouette Coefficient
score = silhouette_score(data, labels)
print(f"Silhouette Coefficient: {score}")

获得结果Silhouette Coefficient: 0.46761904761904766

3.DBI（Davies-Bouldin Index）

Davies-Bouldin Index（DBI）是一种用于评估聚类结果的指标，它通过考虑簇内的紧密度和簇间的分离度来提供一个聚类质量的度量。DBI 的计算方法如下：

对于每个簇 $i$ ，计算以下两个值：

$R_{i}$ 表示簇 $i$ 中所有样本到簇质心的平均距离（簇内平均距离）。
对于所有不同于簇 $i$ 的簇 $j$ ，计算簇 $i$ 的质心与簇 $j$ 的质心之间的距离 $d (i, j)$ 。

对于簇 $i$ ，计算 DBI 如下：
$DB_{i}=\frac{1}{K-1}∑^K_{j=1,j!=j}(\frac{R_{i}+R_{j}}{d(i,j)})$
最终的 Davies-Bouldin Index 是所有簇的 $DB_{i}$ 的最大值。DBI 的取值范围是 $[0, + \infty)$ ，越小表示聚类结果越好。

在Python中，你可以使用scikit-learn库来计算Davies-Bouldin Index（DBI）。scikit-learn提供了一个名为davies_bouldin_score的函数，可以方便地计算给定数据集和聚类结果的DBI。

from sklearn.metrics import davies_bouldin_score
from sklearn.cluster import KMeans
import numpy as np

# 假设 data, labels 已经定义

# 示例数据
data = np.array([[1, 2], [3, 4], [5, 6], [7, 8], [9, 10]])
labels = np.array([0, 0, 1, 1, 1])  # 每个数据点所属的簇

# 使用KMeans聚类算法进行聚类
kmeans = KMeans(n_clusters=2, random_state=0).fit(data)
labels = kmeans.labels_

# 计算DBI
score = davies_bouldin_score(data, labels)
print(f"Davies-Bouldin Index: {score}")

输出Davies-Bouldin Index:0.467

4.CH（Calinski-Harabasz）指数

Calinski-Harabasz指数（CH指数）是一种用于评估聚类结果的指标，它通过比较簇内的紧密度与簇间的分离度来提供一个聚类质量的度量。CH指数的计算方法基于以下公式：
$CH=\frac{B(k)}{W(k)}*\frac{N-k}{k-1}$
其中：

$B (k)$ 是簇间的方差（簇间平方和）。
$W (k)$ 是簇内的方差（簇内平方和）。
$N$ 是样本总数。
$k$ 是簇的数量。

具体计算方法如下：

计算簇内平方和（Within-Cluster Sum of Squares $W (k)$ :对于每个簇 $C_{i}$ ,计算簇内所有样本到簇质心的距离的平方和，然后对所有簇的结果进行求和。
$W(k)=∑^k_{i=1}∑_{x∈C}||x-μ_{i}||^2$
其中 $x-μ_{i}||^2$ 是样本 $i$ 到簇 $C_{i}$ 的质心 $μ_{i}$ 的距离。

计算簇间平方和（Between-Cluster Sum of Squares） $B (K)$ :计算所有簇的质心之间的距离的平方和。
$B(k)=∑^k_{i=1}n_{i}||μ_{i}-μ||^2$
其中 $n_{i}$ 是簇 $C_{i}$ 中的样本数量，μ 是所有样本的均值， $μ_{i}$ 是簇 $C_{i}$ 的质心。具体来说：

CH指数越大，表示簇内的样本之间越紧密，簇之间的间隔越大，说明聚类效果越好。
CH指数越小，表示簇内的样本之间越松散，簇之间的间隔越小，可能是由于聚类数量过多或者聚类质量不佳。

根据CH指数来选择最佳的K值的一般思路是：

对于给定的数据集，尝试不同的K值，分别进行聚类。
对每个K值计算对应的CH指数。
选择具有最大CH指数的K值，因为这表示了最优的聚类效果。
需要注意的是，选择K值时不一定选择CH指数最大的K值，还需要结合实际业务需求和对聚类结果的理解来综合考虑。

Python代码实现如下：

from sklearn.metrics import calinski_harabasz_score
from sklearn.cluster import KMeans
import numpy as np

# 假设 data, labels 已经定义

# 示例数据
data = np.array([[1, 2], [3, 4], [5, 6], [7, 8], [9, 10]])
labels = np.array([0, 0, 1, 1, 1])  # 每个数据点所属的簇

# 使用KMeans聚类算法进行聚类
kmeans = KMeans(n_clusters=2, random_state=0).fit(data)
labels = kmeans.labels_

# 计算CH指数
score = calinski_harabasz_score(data, labels)
print(f"Calinski-Harabasz Index: {score}")