引言

从本节开始，将介绍$\text{Sigmoid}$信念网络。

回顾：贝叶斯网络的因子分解

$\text{Sigmoid}$信念网络，其本质上就是 $\text{Sigmoid}$贝叶斯网络，这说明它是一个有向图模型。在概率图模型——贝叶斯网络的结构表示中介绍过，如果使用贝叶斯网络描述概率图结构，这意味着变量/特征之间存在显式的因果关系。
如果给定一个贝叶斯网络，可以根据该结构直接写出该模型的结构表示(Representation)。已知一个贝叶斯网络表示如下：
也可称作图中变量的‘联合概率分布’/‘概率密度函数’~

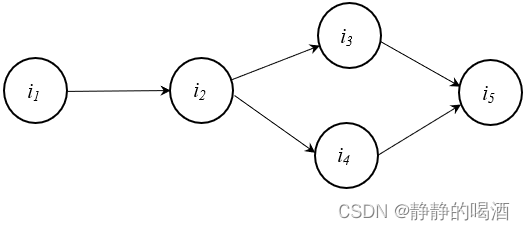
那么该模型中变量的联合概率分布$\mathcal{P}(\mathcal{I})$可表示为：
$i_3,i_4\mid i_2$属于同父结构，因此可以展开，而$i_5\mid i_3,i_4$属于$\mathcal{V}$型结构，无法展开。
$$\begin{array}{rl}\mathcal{P}(\mathcal{I})& =\mathcal{P}(i_1,i_2,i_3,i_4,i_5)\\ & =\mathcal{P}(i_2\mid i_1)\cdot \mathcal{P}(i_3,i_4\mid i_2)\cdot \mathcal{P}(i_5\mid i_3,i_4)\\ & =\mathcal{P}(i_2\mid i_1)\cdot \mathcal{P}(i_3\mid i_2)\cdot \mathcal{P}(i_4\mid i_2)\cdot \mathcal{P}(i_5\mid i_3,i_4)\end{array}$$

Sigmoid信念网络

单从名称中观察，信念网络指的就是贝叶斯网络；$\text{Sigmoid}$自然是指$\text{Sigmoid}$函数：
$$\sigma (x)=\frac{1}{1+\exp (-x)}$$
它的模型结构，以及模型表示是如何产生的？已知一个$\text{Sigmoid}$信念网络表示如下：

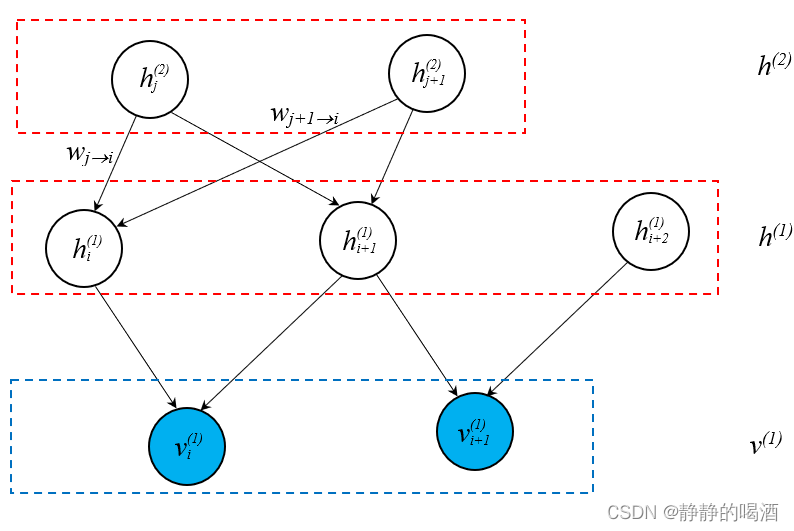
其中蓝色结点表示观测变量，蓝色虚线框中的结点表示观测变量层；同理，白色结点表示隐变量，整个隐变量包含两个隐变量层。
$\text{Neal}$在1990年提出该模型时，将玻尔兹曼机、贝叶斯网络相结合产生的模型产物。该模型的优势在于：

• $\text{Sigmoid}$信念网络是有向图模型，因此在采样过程中，根据结点之间的因果关系 可以很容易地找到采样顺序(祖先采样方法)；根节点(入度为零)开始，按照拓扑排序的顺序进行采样。
  从根节点开始采样，与根节点相连的其他结点之间属于同父结构。一旦根节点被采样(被观测)，其相连结点之间条件独立。
• 和前馈神经网络的函数逼近定理类似，如果隐藏层数量$\ge 1$层，从观测变量角度，它可以逼近任意二分类离散分布。

关于随机变量集合$\mathcal{S}$的描述如下：
$v$表示观测变量集合;$h$表示隐变量集合。
需要注意的点：

• 这里的小括号上标并非表示样本编号，而是关于层的编号。如$h_{i+1}^{(1)}$表示第$1$个隐藏层中编号$i+1$的随机变量结点。当然，推导过程中的小括号是样本编号~
• 与玻尔兹曼机、受限玻尔兹曼机相同，概率模型中的每个结点均服从‘伯努利分布’。

S = { v , h } = { v ( 1 ) , h ( 1 ) , h ( 2 ) } = { v i ( 1 ) , v i + 1 ( 1 ) , h i ( 1 ) , h i + 1 ( 1 ) , h i + 2 ( 1 ) , h j ( 2 ) , h j + 1 ( 2 ) } \begin{aligned} \mathcal S = \{v,h\} & = \{v^{(1)},h^{(1)},h^{(2)}\} \\ & = \{v_i^{(1)},v_{i+1}^{(1)},h_{i}^{(1)},h_{i+1}^{(1)},h_{i+2}^{(1)},h_{j}^{(2)},h_{j+1}^{(2)}\} \end{aligned} S={v,h}​={v(1),h(1),h(2)}={vi(1)​,vi+1(1)​,hi(1)​,hi+1(1)​,hi+2(1)​,hj(2)​,hj+1(2)​}​
由于这是一个贝叶斯网络，我们可以通过结点之间的因果关系描述出该图的联合概率分布：
在贝叶斯网络结构表示中介绍过,受先找到入度为零的结点，再通过拓扑排序方式寻找各结点的后验概率信息。
$$\begin{array}{rl}\mathcal{P}(\mathcal{S})& =\mathcal{P}(v_i^{(1)},v_{i+1}^{(1)},h_i^{(1)},h_{i+1}^{(1)},h_{i+2}^{(1)},h_j^{(2)},h_{j+1}^{(2)})\\ & =\mathcal{P}(h_j^{(2)})\cdot \mathcal{P}(h_{j+1}^{(2)})\cdot \mathcal{P}(h_i^{(1)}\mid h_j^{(2)},h_{j+1}^{(2)})\cdot \mathcal{P}(h_{i+1}^{(1)}\mid h_j^{(2)},h_{j+1}^{(2)})\cdot \mathcal{P}(v_i^{(1)}\mid h_i^{(1)},h_{i+1}^{(1)})\cdot \mathcal{P}(h_{i+2}^{(1)})\cdot \mathcal{P}(v_{i+1}^{(1)}\mid h_{i+1}^{(1)},h_{i+2}^{(1)})\end{array}$$
基于$\text{Sigmoid}$信念网络的定义，以$h_i^{(1)}$结点为例，它的概率分布表示如下：

• 由于$h_i^{(1)}$与$h_j^{(2)},h_{j+1}^{(2)}$存在因果关系。因此，这个‘概率分布’明显指的是条件概率分布$\mathcal{P}(h_i^{(1)}\mid h_j^{(2)},h_{j+1}^{(2)})$.
• 提醒：概率分布描述中的$h_j^{(2)},h_{j+1}^{(2)}$并不是概率分布结果，而是具体的随机变量取值： h j ( 2 ) , h j + 1 ( 2 ) ∈ { 0 , 1 } h_j^{(2)},h_{j+1}^{(2)} \in \{0,1\} hj(2)​,hj+1(2)​∈{0,1}.
• $\sigma (-x)=1-\sigma (x)$是$\text{Sigmoid}$函数自身的性质~
  $$\mathcal{P}(h_i^{(1)}\mid h_j^{(2)},h_{j+1}^{(2)})=\{\begin{array}{l}\mathcal{P}(h_i^{(1)}=1\mid h_j^{(2)},h_{j+1}^{(2)})=\sigma \left({\mathcal{W}}_{j\to i}\cdot h_j^{(2)}+{\mathcal{W}}_{j+1\to i}\cdot h_{j+1}^{(2)}\right)\\ \begin{array}{rl}\mathcal{P}(h_i^{(1)}=0\mid h_j^{(2)},h_{j+1}^{(2)})& =1-\sigma \left({\mathcal{W}}_{j\to i}\cdot h_j^{(2)}+{\mathcal{W}}_{j+1\to i}\cdot h_{j+1}^{(2)}\right)\\ & =\sigma \left[-\left({\mathcal{W}}_{j\to i}\cdot h_j^{(2)}+{\mathcal{W}}_{j+1\to i}\cdot h_{j+1}^{(2)}\right)\right]\end{array}\end{array}$$

如果将其表示成通式的话，模型中某结点$h_i$的概率分布可表示如下：
${\sum }_{j\to i}{\mathcal{W}}_{j\to i}\cdot h_j$表示模型中指向$h_i$的结点们与对应参数的线性组合结果。
$$\mathcal{P}(h_i\mid h_j;j\to i)=\{\begin{array}{l}\mathcal{P}(h_i=1\mid h_j;j\to i)=\sigma \left({\sum }_{j\to i}{\mathcal{W}}_{j\to i}\cdot h_j\right)\\ \mathcal{P}(h_i=0\mid h_j;j\to i)=\sigma \left(-{\sum }_{j\to i}{\mathcal{W}}_{j\to i}\cdot h_j\right)\end{array}$$
基于随机变量$h_i$的伯努利分布性质，将上述分段函数描述为一个公式：
$$\mathcal{P}(h_i\mid h_j;j\to i)=\sigma \left[(2h_i-1)\sum _{j\to i}{\mathcal{W}}_{j\to i}\cdot h_j\right]$$

关于$\text{Sigmoid}$信念网络的学习任务(Learning)，Neal当时提出使用MCMC采样的方式对模型参数梯度进行求解。在真实情况下，MCMC采样方式仅能对 随机变量数量较少的模型结构 进行求解。在玻尔兹曼机——基于MCMC的梯度求解中简单介绍过：首先，随着随机变量数量的增加，对应的复杂度也会指数级别地增长；其次，达到平稳分布是极困难的。

重新观察上述$\text{Sigmoid}$信念网络示例：$v_i^{(1)},v_{i+1}^{(1)}$是观测变量的随机变量信息，观测变量是样本提供的，因此和玻尔兹曼机、受限玻尔兹曼机一样，$v_i^{(1)},v_{i+1}^{(1)}$是 可观测的。以$v_i^{(1)}$为例，在$v_i^{(1)}$被观测的条件下，$h_i^{(1)},h_{i+1}^{(1)}$之间 不是条件独立关系($\mathcal{V}$型结构)，因此关于$h_i^{(1)}$或者$h_{i+1}^{(1)}$的后验概率分布无法求解。

下面将求解模型参数的对数似然梯度，观察对数似然梯度与后验概率之间存在什么关联关系。

对数似然梯度推导过程

关于某随机变量结点的后验概率分布可表示为：

• 注意，这里的$s_i$无论是观测变量，还是隐变量，都和其父节点之间存在这种关联关系。
• 为了推导过程方便，将线性计算中的偏置项$b$归纳仅$\mathcal{W}$中。
• 为了符号使用方便，将$i$改成了$k$.
  $$\{\begin{array}{l}\mathcal{P}(s_k\mid s_j;j\to k)=\sigma \left[s_k^{\ast }\cdot {\sum }_{j\to k}{\mathcal{W}}_{j\to k}\cdot s_j\right]\\ s_k^{\ast }=2s_k-1\end{array}$$

对应地，关于随机变量$\mathcal{S}$的联合概率分布通式$\mathcal{P}(\mathcal{S})$可表示为：
$$\mathcal{P}(\mathcal{S})=\prod _{s_k\in \mathcal{S}}\mathcal{P}(s_k\mid s_j;j\to k)$$
关于观测变量的对数似然(Log-Likelihood)可表示为：
这里依然需要场景构建：数据集合$\mathcal{V}$包含$|\mathcal{V}|=N$个样本 { v ( 1 ) , v ( 2 ) , ⋯   , v ( ∣ V ∣ ) } \{v^{(1)},v^{(2)},\cdots,v^{(|\mathcal V|)}\} {v(1),v(2),⋯,v(∣V∣)},并且每一个样本都可看做随机变量集合(观测变量)$v$的一种具体表示。
$$\text{Log-Likelihood: }\sum _{v^{(i)}\in \mathcal{V}}\log \mathcal{P}(v^{(i)})$$
对某一权重${\mathcal{W}}_{j\to i}$的梯度可表示为：
这里的权重${\mathcal{W}}_{j\to i}$是指‘某一随机变量’$s_j$指向'随机变量'$s_i$的权重信息
$$\frac{\partial }{\partial {\mathcal{W}}_{j\to i}}\left[\sum _{v^{(i)}\in \mathcal{V}}\log \mathcal{P}(v^{(i)})\right]$$
根据链式求导法则，对上式进行展开：

• 使用‘牛顿-莱布尼兹公式’，将积分(连加号)与梯度符号交换位置。
• 为了后续推导方便，将对数似然梯度使用$\Delta$进行表示。
  $$\begin{array}{rl}\Delta & =\frac{\partial }{\partial {\mathcal{W}}_{j\to i}}\left[\sum _{v^{(i)}\in \mathcal{V}}\log \mathcal{P}(v^{(i)})\right]\\ & =\sum _{v^{(i)}\in \mathcal{V}}\frac{\partial }{\partial {\mathcal{W}}_{j\to i}}\log \mathcal{P}(v^{(i)})\\ & =\sum _{v^{(i)}\in \mathcal{V}}\frac{1}{\mathcal{P}(v^{(i)})}\cdot \frac{\partial \mathcal{P}(v^{(i)})}{\partial {\mathcal{W}}_{j\to i}}\end{array}$$

引入$v^{(i)}$对应在$\text{Sigmoid}$信念网络中的隐变量集合$h^{(i)}$：

• 这里同样使用‘牛顿-莱布尼兹公式’。
• 根据条件概率公式，将$\frac{1}{\mathcal{P}(v^{(i)})}=\frac{\mathcal{P}(h^{(i)}\mid v^{(i)})}{\mathcal{P}(v^{(i)},h^{(i)})}$代入式子中。
• 而$\mathcal{P}(v^{(i)},h^{(i)})$实际上就是某一样本的随机变量集合(隐变量、观测变量)的联合概率分布。这里对应使用符号${\mathcal{S}}^{(i)}$进行表示。
  $$\begin{array}{rl}\Delta & =\sum _{v^{(i)}\in \mathcal{V}}\frac{1}{\mathcal{P}(v^{(i)})}\cdot \frac{\partial }{\partial {\mathcal{W}}_{j\to i}}\left[\sum _{h^{(i)}}\mathcal{P}(v^{(i)},h^{(i)})\right]\\ & =\sum _{v^{(i)}\in \mathcal{V}}\sum _{h^{(i)}}\frac{1}{\mathcal{P}(v^{(i)})}\cdot \frac{\partial }{\partial {\mathcal{W}}_{j\to i}}\mathcal{P}(v^{(i)},h^{(i)})\\ & =\sum _{v^{(i)}\in \mathcal{V}}\sum _{h^{(i)}}\frac{\mathcal{P}(h^{(i)}\mid v^{(i)})}{\mathcal{P}(v^{(i)},h^{(i)})}\cdot \frac{\partial }{\partial {\mathcal{W}}_{j\to i}}\mathcal{P}(v^{(i)},h^{(i)})\\ & =\sum _{v^{(i)}\in \mathcal{V}}\sum _{h^{(i)}}\mathcal{P}(h^{(i)}\mid v^{(i)})\cdot \frac{1}{\mathcal{P}({\mathcal{S}}^{(i)})}\cdot \frac{\partial \mathcal{P}({\mathcal{S}}^{(i)})}{\partial {\mathcal{W}}_{j\to i}}\end{array}$$\

将$\mathcal{P}({\mathcal{S}}^{(i)})$使用联合概率分布通式展开，有：

• 很明显，${\mathcal{S}}^{(i)}$中有多少个随机变量，${\prod }_{s_k^{(i)}\in {\mathcal{S}}^{(i)}}\mathcal{P}(s_k^{(i)}\mid s_j^{(i)};j\to k)$中就有多少项乘法。但与${\mathcal{W}}_{j\to i}$相关的项只有$\mathcal{P}(s_i^{(i)}\mid s_j^{(i)};j\to i)$一项，其余项均可视作常数。
• 使用符号$\Omega ={\prod }_{s_k^{(i)}\ne s_i^{(i)}\in {\mathcal{S}}^{(i)}}\mathcal{P}(s_k^{(i)}\mid s_j^{(i)};j\to k)$表示除去$\mathcal{P}(s_i^{(i)}\mid s_j^{(i)};j\to i)$这一项之外的其他项的乘积。
  $$\begin{array}{rl}\Delta & =\sum _{v^{(i)}\in \mathcal{V}}\sum _{h^{(i)}}\mathcal{P}(h^{(i)}\mid v^{(i)})\cdot \frac{1}{{\prod }_{s_k^{(i)}\in {\mathcal{S}}^{(i)}}\mathcal{P}(s_k^{(i)}\mid s_j^{(i)};j\to k)}\cdot \frac{\partial }{\partial {\mathcal{W}}_{j\to i}}\left[\prod _{s_k^{(i)}\in {\mathcal{S}}^{(i)}}\mathcal{P}(s_k^{(i)}\mid s_j^{(i)};j\to k)\right]\\ & =\sum _{v^{(i)}\in \mathcal{V}}\sum _{h^{(i)}}\mathcal{P}(h^{(i)}\mid v^{(i)})\cdot \frac{1}{\Omega \cdot \mathcal{P}(s_i^{(i)}\mid s_j^{(i)};j\to i)}\cdot \left[\Omega \cdot \frac{\partial }{\partial {\mathcal{W}}_{j\to i}}\mathcal{P}(s_i^{(i)}\mid s_j^{(i)};j\to i)\right]\\ & =\sum _{v^{(i)}\in \mathcal{V}}\sum _{h^{(i)}}\mathcal{P}(h^{(i)}\mid v^{(i)})\cdot \frac{1}{\mathcal{P}(s_i^{(i)}\mid s_j^{(i)};j\to i)}\cdot \left[\frac{\partial }{\partial {\mathcal{W}}_{j\to i}}\mathcal{P}(s_i^{(i)}\mid s_j^{(i)};j\to i)\right]\end{array}$$

至此，发现$\mathcal{P}(s_i^{(i)}\mid s_j^{(i)};j\to i)$实际上就是结点的后验概率分布。那么将$\text{Sigmoid}$代入，有：
$$\begin{array}{r}\Delta =\sum _{v^{(i)}\in \mathcal{V}}\sum _{h^{(i)}}\mathcal{P}(h^{(i)}\mid v^{(i)})\cdot \frac{1}{\sigma \left[(2s_i^{(i)}-1)\cdot {\sum }_{j\to i}{\mathcal{W}}_{j\to i}\cdot s_j^{(i)}\right]}\left\{\frac{\partial }{\partial {\mathcal{W}}_{j\to i}}\sigma \left[(2s_i^{(i)}-1)\cdot \sum _{j\to i}{\mathcal{W}}_{j\to i}\cdot s_j^{(i)}\right]\right\}\end{array}$$
依然使用链式求导法则进行求导。观察关于$\text{Sigmoid}$函数的导数：
$$\begin{array}{rl}\frac{\partial }{\partial x}\left[\sigma (x)\right]& =\frac{e^{-x}}{(1+e^{-x}{)}^2}=\frac{1}{1+e^{-x}}\cdot \frac{e^{-x}}{1+e^{-x}}\\ & =\sigma (x)\cdot \sigma (-x)\end{array}$$
那么上式$\Delta$可表示为：
同上，关于${\sum }_{j\to i}{\mathcal{W}}_{j\to i}\cdot s_j^{(i)}$对${\mathcal{W}}_{j\to i}$求解偏导，实际上只有一项与${\mathcal{W}}_{j\to i}$相关，与其他项无关，均视作常数。
p.s. 这里$j$下标还是用重复了~
$$\begin{array}{r}\Delta =\sum _{v^{(i)}\in \mathcal{V}}\sum _{h^{(i)}}\mathcal{P}(h^{(i)}\mid v^{(i)})\cdot \frac{1}{\sigma \left[(2s_i^{(i)}-1)\cdot {\sum }_{j\to i}{\mathcal{W}}_{j\to i}\cdot s_j^{(i)}\right]}\cdot \sigma \left[(2s_i^{(i)}-1)\cdot \sum _{j\to i}{\mathcal{W}}_{j\to i}\cdot s_j^{(i)}\right]\cdot \sigma \left[-(2s_i^{(i)}-1)\cdot \sum _{j\to i}{\mathcal{W}}_{j\to i}\cdot s_j^{(i)}\right]\cdot (2s_i^{(i)}-1)\cdot s_j^{(i)}\end{array}$$
该消掉的消掉，最后整理有：
$$\begin{array}{rl}\frac{\partial }{\partial {\mathcal{W}}_{j\to i}}\left[\sum _{v^{(i)}\in \mathcal{V}}\log \mathcal{P}(v^{(i)})\right]& =\sum _{v^{(i)}\in \mathcal{V}}\sum _{h^{(i)}}\mathcal{P}(h^{(i)}\mid v^{(i)})\cdot \sigma \left[-(2s_i^{(i)}-1)\cdot \sum _{j\to i}{\mathcal{W}}_{j\to i}\cdot s_j^{(i)}\right]\cdot (2s_i^{(i)}-1)\cdot s_j^{(i)}\end{array}$$

梯度求解过程中的问题

至此，观察关于${\mathcal{W}}_{j\to i}$的梯度，其中包含一个关于隐变量集合的后验概率$\mathcal{P}(h^{(i)}\mid v^{(i)})$。因为$\mathcal{V}$型结构，给定观测变量条件下，根本不是条件独立，因此没有办法对$\mathcal{P}(h^{(i)}\mid v^{(i)})$直接进行求解。

针对于小规模的随机变量集合，可以使用MCMC方法进行求解：

• 针对‘对数似然’，这里乘以一个常数$\frac{1}{N}$，之前拉下了，对梯度方向不产生影响。
• 依然是蒙特卡洛方法的逆推公式~
  $$\begin{array}{rl}\frac{\partial }{\partial {\mathcal{W}}_{j\to i}}\left[\frac{1}{N}\sum _{v^{(i)}\in \mathcal{V}}\log \mathcal{P}(v^{(i)})\right]& =\frac{1}{N}\sum _{v^{(i)}\in \mathcal{V}}{\mathbb{E}}_{{\mathcal{P}}_{model}(h^{(i)}\mid v^{(i)})}\left[\sigma \left(-(2s_i^{(i)}-1)\cdot \sum _{j\to i}{\mathcal{W}}_{j\to i}\cdot s_j^{(i)}\right)\cdot (2s_i^{(i)}-1)\cdot s_j^{(i)}\right]\\ & \approx {\mathbb{E}}_{{\mathcal{P}}_{data}(v^{(i)}\in \mathcal{V})}\left\{{\mathbb{E}}_{{\mathcal{P}}_{model}(h^{(i)}\mid v^{(i)})}\left[\sigma \left(-(2s_i^{(i)}-1)\cdot \sum _{j\to i}{\mathcal{W}}_{j\to i}\cdot s_j^{(i)}\right)\cdot (2s_i^{(i)}-1)\cdot s_j^{(i)}\right]\right\}\\ & =\{\begin{array}{l}{\mathbb{E}}_{{\mathcal{P}}_{data}}\left[\sigma \left(-(2s_i^{(i)}-1)\cdot {\sum }_{j\to i}{\mathcal{W}}_{j\to i}\cdot s_j^{(i)}\right)\cdot (2s_i^{(i)}-1)\cdot s_j^{(i)}\right]\\ {\mathcal{P}}_{data}\Rightarrow {\mathcal{P}}_{data}(v^{(i)}\in \mathcal{V})\cdot {\mathcal{P}}_{model}(h^{(i)}\mid v^{(i)})\end{array}\end{array}$$

通过观察可以发现，这种描述方式和玻尔兹曼机——基本介绍中正相部分的描述格式基本相同。如果说一句总结的话，那就是 使用传统方式求解模型参数梯度，梯度中包含隐变量的后验概率，因而没有办法直接求解。可以通过MCMC方式采样近似求解，它的弊端这里就不多说了。

下一节将介绍醒眠算法

相关参考：
(系列二十六)Sigmoid Belief Network1-背景介绍
(系列二十六)Sigmoid Belief Network2- gradient of log-likelihood
(系列二十六)Sigmoid Belief Network2- gradient of log-likelihood续