第一题:两种排序方法(网易)两种排序方法_牛客题霸_牛客网
题目描述:考拉有N个字符串,任意两个字符串的长度都不是相同的,考拉现在学习到了两种字符串的排序方法
1)根据字符串的字典序排序,比如说
"car"<"carriage"<"cats"<"doggies"<"koala"
2)根据字符串的长度排序,例如:
"car" < "cats" < "koala" < "doggies" < "carriage"
考拉想知道自己的这些字符串排列顺序是否满足这两种排序方法,考拉要忙着吃树叶,所以需要你来帮忙验证。思路:
1)我们可以单独写两个函数返回值是false,来分别进行判断是否按照字段排序和分别按照长度来进行排序
2)如果是按照字段进行排序那么使用compareTo,如果是按照长度来进行排序的话那就调用字符串的length()方法
import java.util.Scanner; import java.util.*; // 注意类名必须为 Main, 不要有任何 package xxx 信息 public class Main { public static boolean IsArt(String[] array){ for(int i=1;i<array.length;i++){ if(array[i-1].compareTo(array[i])>0){ return false; } } return true; } public static boolean IsLength(String[] array){ for(int i=1;i<array.length;i++){ if(array[i].length()<array[i-1].length()){ return false; } } return true; } public static void main(String[] args) { Scanner scanner=new Scanner(System.in); int n=Integer.parseInt(scanner.nextLine()); String[] array=new String[n]; for(int i=0;i<array.length;i++){ array[i]=scanner.nextLine(); } // System.out.println(Arrays.toString(array)); boolean flag1=IsLength(array); boolean flag2=IsArt(array); if(flag1==true&&flag2==false){ System.out.println("lengths"); }else if(flag1==false&&flag2==true){ System.out.println("lexicographically"); }else if(flag1==true&&flag2==true){ System.out.println("both"); }else{ System.out.println("none"); } } }扩展一下:判断一个整型数组是否是升序排列?
package com.example.demo; import java.util.Scanner; import java.util.*; // 注意类名必须为 Main, 不要有任何 package xxx 信息 public class Main { public static void main(String[] args) { Scanner scanner=new Scanner(System.in); int n=scanner.nextInt(); int[] array=new int[n]; for(int i=0;i<n;i++){ array[i]=scanner.nextInt(); } for(int i=0;i<array.length-1;i++){//因为i+1最终会导致数组越界 if(array[i]>array[i+1]){ System.out.println("当前数组不是升序排列"); return; } } System.out.println("当前数组是升序排列"); } }for(int i=1;i<array.length;i++){//因为i+1最终会导致数组越界 if(array[i]<array[i-1]){ System.out.println("当前数组不是升序排列"); return; } } System.out.println("当前数组是升序排列");第二题:两个数的最小公倍数:最小公倍数__牛客网
第一种方法:从最大的数开始进行相加,但是时间复杂度是O(N),众所周知,最小公倍数
import java.util.*; public class Main{ public static int GetMax(int m,int n){ return m>n?m:n; } public static void main(String[] args){ Scanner scanner=new Scanner(System.in); int m=scanner.nextInt(); int n=scanner.nextInt(); int max=GetMax(m,n); for(int i=max;i<=Integer.MAX_VALUE;i++){ if(i%m==0&&i%n==0){ System.out.println(i); break; } } } }第二种方法:两个数的最小公倍数等于-->(A,B)两个数的最小公倍数是A*B/(A和B的最大公约数)
但是我们要注意:A和B两个数的相乘可能大于Integer的范围
import java.util.*; public class Main{ public static void main(String[] args){ Scanner scanner=new Scanner(System.in); int a=scanner.nextInt(); int b=scanner.nextInt(); if(a==b){ System.out.println(a); return; } int m=a; int n=b; int model=m%n; while(model!=0){ m=n; n=model; model=m%n; } System.out.println(a*b/n); } }
编程题第三题:另类加法另类加法__牛客网
求出两个数的和,但是不能使用"+"运算
思路:我们在这个题中主要用到的运算符就是异或
异或:相同为0不同为1
异或:两个相同的十进制数异或,结果是0,一个数字和0异或,结果还是这个数,不考虑进为
1)我们还是需要进行注意:两个二进制位相异或的结果,就是两个数对应相加的结果,但是我们不会考虑进位
比如说1的二进制是0001,2的二进制是0010,但是1+2=3,我们对应的3的二进制位是0011
2)两个二进制位按位与后左移1位的结果,是两个数相加进位之后的结果
比如说1和2两个数(0001&0010)=0000,那就说明没有进位
比如说2和3两个数异或的结果是:0001
2和3两个数按位与左移一位的结果是:0100
假设我们此时还是想算两个数的和:那么就把把上面按位与和按位异或的结果在进行异或(就相当于是相加了),同时我们还需要进行判断按为与之后的结果是不是为0
public class UnusualAdd { public int addAB(int A, int B) { if(B==0){ return A; } int sum=A^B; int carray=(A&B)<<1; while(carray!=0){ sum=A^B; carray=(A&B)<<1; A=sum; B=carray; } return sum; } }如果说实在不理解的话来举一个例子,比如说我们现在计算7和8的和,注意比特位一共是32位
A:7的二进制序列是111
B:6的二进制序列是110
6%2=0,6/2=3
3%2=1,3/2=1
1%2=1,1/2=1
用stringBuiler进行拼接再进行翻转,就可以得到6的二进制序列
1)sum=111^110=0001
2)carray=(111&110)<<1=1100(此时可以说最终的结果就是1101)
3)A=sum=0001,B=carray=1100
4)sum=A^B=1101
carray=0000,说明此时没有余数,那么最终的结果就是1101
编程题第四题:走方格的方案数_牛客题霸_牛客网
题目大概叙述:请你计算n*m的棋盘格子,n是横向的格子数,m是竖向的格子数,现在要求你去求出从棋盘左上角出发沿着边缘线从左上角走到右下角,总共有多少种走法?况且不能走回头路
要求往右或者往下走,不能往左或者往上走
我们来看一下一些数据的特殊情况:
1)m=1,n=1,现在主要是两条路径
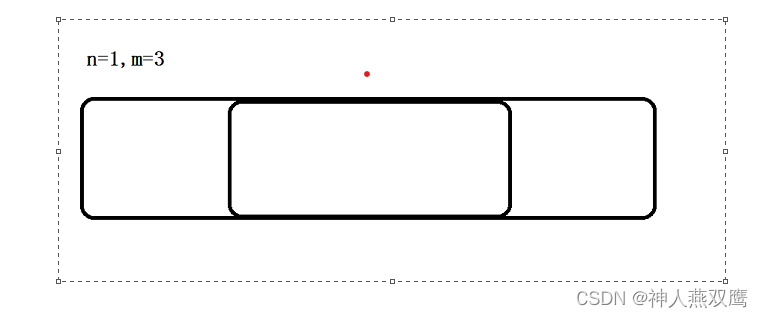
2)此时让n=1,m>1(比如说m=3),此时我们发现路径条数是4条,也就是m+n
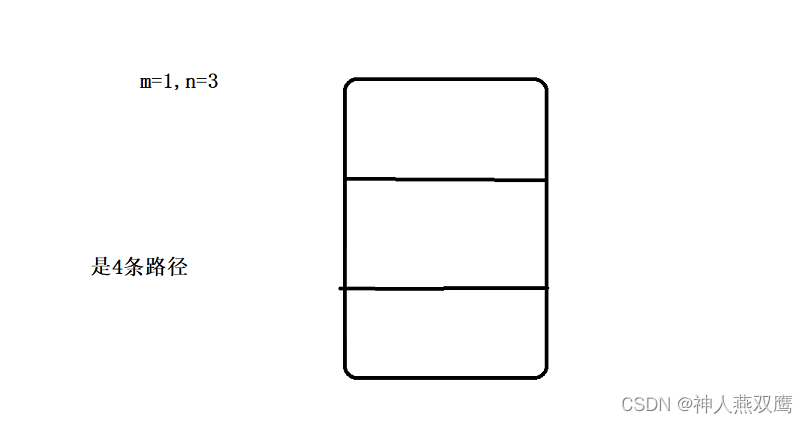
3)此时我们让n>1,m=1,比如说现在n=3,m=1
总结:
1)当我们的N=1,并且M>=1,那么路径的总条数就是m+n
2)当我们的M=1,并且N>=1,那么路径的总条数就是m+n
3)此时n>1,m>1的时候,此时我们求的路径的总条数就可以抽象成:
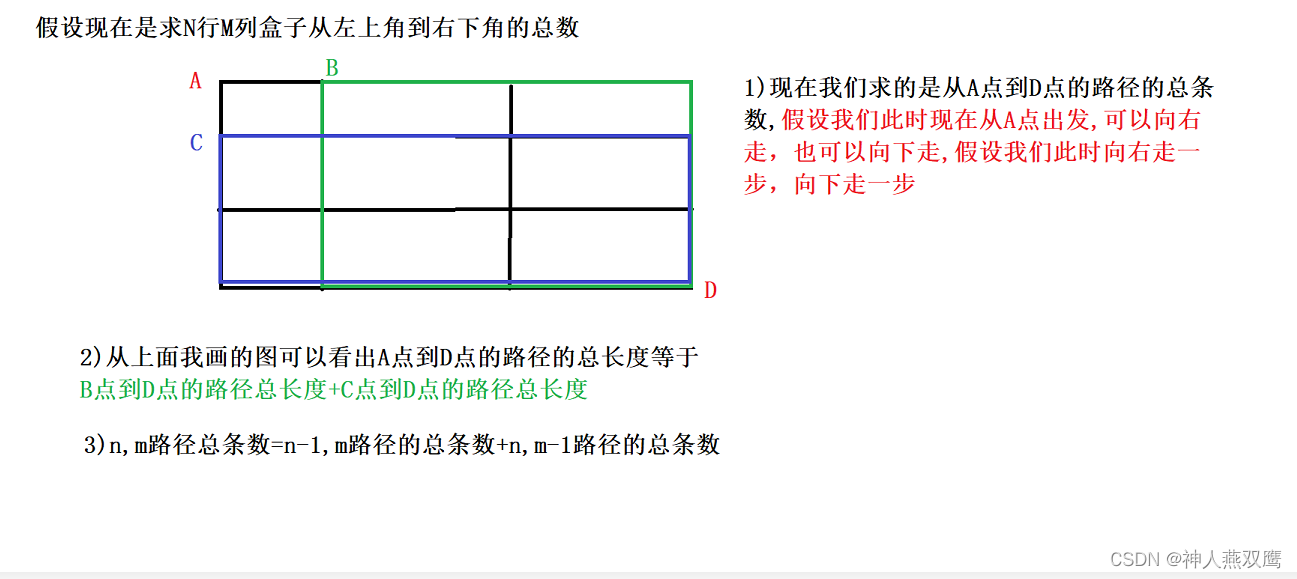
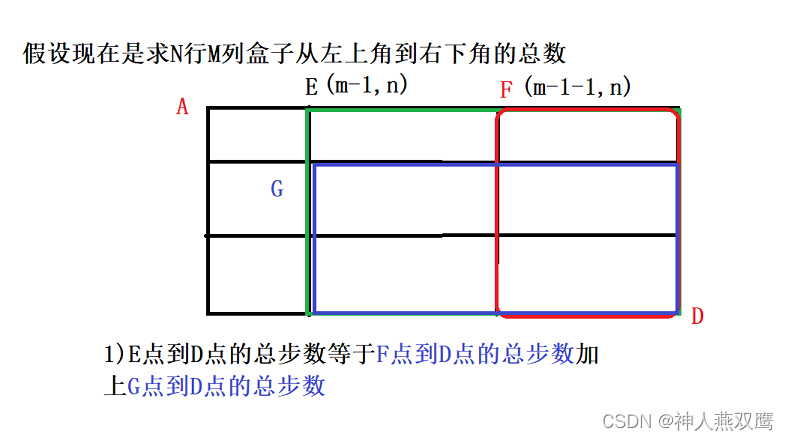
现在我们具体的再来分析一下,逐步地进行抽象,我们先把整体分为从左上角到右下角的步数分成
从出发点向右走一步的那个点到终点的所形成的长方形的总步数+向下走一步的那个点到终点所形成的长方形到终点的步数
此时我们再以绿色的点E为基准,这个点到D点的距离就相当于是:
1)从E点向右走一步到达的E点到终点D所最终的步数+从E点向下走一步到达的G点到终点D点最终所走的步数
2)但是我们最终发现,在不断地进行细分的时候,发现红色的小框的行数已经变成了1,那么此时我们就不需要在进行分解,直接可以算出总步数是m+n
3)但是上图中那一个蓝色的部分就是还是需要在进行分解
当我们的行数或者列数为1的时候,就是终止条件,所以直接返回m+n就可以了
import java.util.Scanner; // 注意类名必须为 Main, 不要有任何 package xxx 信息 public class Main { public static int func(int m,int n){ //如果说行数或者列数其中有一行大于1的,直接返回m+n if(m==1||n==1){ return m+n; } //处理n大于1,m大于1的这种情况 return func(m-1,n)+func(m,n-1); } public static void main(String[] args) { Scanner scanner=new Scanner(System.in); int m=scanner.nextInt(); int n=scanner.nextInt(); int result=func(m,n); System.out.println(result); } }自己可以画一下递归图,比如说写一个4行5列的总路径数


![[Square 2022] Hard Copy 复现](https://img-blog.csdnimg.cn/6cd71c6576b24c4081f6be6a84c88d3c.jpeg)