文章目录
- 枚举算法
- 1、铺地毯
- 2、回文日期
枚举算法
枚举算法是我们在日常中使用到的最多的一个算法,它的核心思想就是:枚举所有的可能。
枚举法的本质就是从所有候选答案中去搜索正确的解,使用该算法需要满足两个条件:
(1)可预先确定候选答案的数量;
(2)候选答案的范围在求解之前必须有一个确定的集合。
1、铺地毯
NC16593 铺地毯
题目描述
为了准备一个独特的颁奖典礼,组织者在会场的一片矩形区域(可看做是平面直角坐标系的第一象限)铺上一些矩形地毯。一共有n张地毯,编号从1到n。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设,后铺的地毯覆盖在前面已经铺好的地毯之上。地毯铺设完成后,组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意:在矩形地毯边界和四个顶点上的点也算被地毯覆盖。
输入描述:
第一行,一个整数n,表示总共有n张地毯。
接下来的n行中,第i+1行表示编号i的地毯的信息,包含四个正整数a,b,g,k,每两个整数之间用一个空格隔开,分别表示铺设地毯的左下角的坐标(a,b)以及地毯在x轴和y轴方向的长度。
第n+2行包含两个正整数x和y,表示所求的地面的点的坐标(x,y)。
输出描述:
输出共1行,一个整数,表示所求的地毯的编号;若此处没有被地毯覆盖则输出-1。
示例1
输入
3 1 0 2 3 0 2 3 3 2 1 3 3 2 2
输出
3
说明
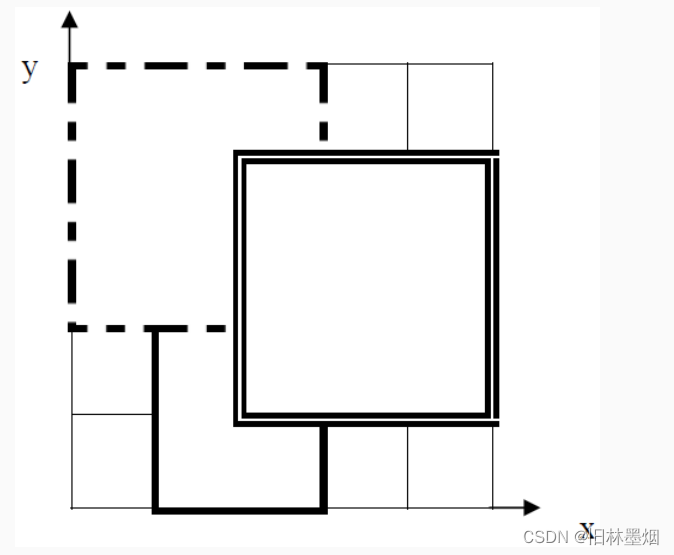
如下图,1号地毯用实线表示,2号地毯用虚线表示,3号用双实线表示,覆盖点(2,2)的最上面一张地毯是3号地毯。
备注:
对于30%的数据,有n≤2;
对于50%的数据,有0≤a,b,g,k≤100;
对于100%的数据,有0≤n≤10,000,0≤a,b,g,k≤100,000。
解题思路:
从下到上枚举地毯,遇到符合条件的地毯就选择该地毯,这样可以保证所选择的地毯是最优的
代码:
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin>>n;
int a[10010][4];
for(int i=0;i<n;i++){
cin>>a[i][0]>>a[i][1]>>a[i][2]>>a[i][3];
}
int x,y;
cin>>x>>y;
int ans=-1;
for(int i=0;i<n;i++){//从下到上枚举所有的地毯
if(x>=a[i][0]&&x<=a[i][0]+a[i][2]&&y>=a[i][1]&&y<=a[i][1]+a[i][3]){
ans=i+1;//如果符合题意就取最优的解
}
}
cout<<ans<<endl;
}
2、回文日期
NC16438 回文日期
题目描述
在日常生活中,通过年、月、日这三个要素可以表示出一个唯一确定的日期。
牛牛习惯用8位数字表示一个日期,其中,前4位代表年份,接下来2位代表月份,最后2位代表日期。显然:一个日期只有一种表示方法,而两个不同的日期的表示方法不会相同。
牛牛认为,一个日期是回文的,当且仅当表示这个日期的8位数字是回文的。现 在,牛牛想知道:在他指定的两个日期之间包含这两个日期本身),有多少个真实存在的日期是回文的。
一个8位数字是回文的,当且仅当对于所有的i ( 1 <=i<= 8 )从左向右数的第i个 数字和第9-i个数字(即从右向左数的第i个数字)是相同的。
例如:
• 对于2016年11月19日,用8位数字20161119表示,它不是回文的。
• 对于2010年1月2日,用8位数字20100102表示,它是回文的。
• 对于2010年10月2日,用8位数字20101002表示,它不是回文的。
每一年中都有12个月份:
其中,1、3、5、7、8、10、12月每个月有31天;4、6、9、11月每个月有30天;而对于2月,闰年时有29天,平年时有28天。
一个年份是闰年当且仅当它满足下列两种情况其中的一种:
1.这个年份是4的整数倍,但不是100的整数倍;
2.这个年份是400的整数倍。
例如:
• 以下几个年份都是闰年:2000、2012、2016。
• 以下几个年份是平年:1900、2011、2014。
输入描述:
输入包括两行,每行包括一个8位数字。
第一行表示牛牛指定的起始日期。
第二行表示牛牛指定的终止日期。
保证datei和都是真实存在的日期,且年份部分一定为4位数字,且首位数字不为0。
保证date1 —定不晚于date2。
输出描述:
输出一行,包含一个整数,表示在date1和date2之间,有多少个日期是回文的。
示例1
输入
20110101
20111231
输出
1
说明
符合条件的日期是20111102。
示例2
输入
20000101
20101231
输出
2
说明
符合条件的日期是20011002和20100102。
备注:
对于60%的数据,满足date1 = date2。
解题思路:
1、一年有365天,那么10000年有3650000天,如果我们枚举所有符合条件的日期,再判断该日期是不是回文串,那么时间复杂度接近10的8次方。这样做不仅麻烦,保守估计也运行超时了
2、我们应该直接构造回文串,日期有8位,那么回文串就只要10000个,枚举完绰绰有余,那么应该如何构造呢,看完下面的表格就差不多明白了
| 数字 | 回文串 |
|---|---|
| 0000 | 00000000 |
| 0001 | 10000001 |
| 0002 | 20000002 |
| 0003 | 30000003 |
| …… | …… |
| 0102 | 20100102 |
| 0103 | 30100103 |
| …… | …… |
| 5014 | 41055014 |
| 5015 | 51055015 |
| …… | …… |
3、想必发现规律了把!我们只需从0枚举到10000,就可以枚举完所有8位数的回文串了,再判断该回文串是不是正确的日期即可
代码:
#include<bits/stdc++.h>
using namespace std;
int main(){
int b[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};//1到12月的天数
string s1,s2;
cin>>s1>>s2;
int a=0;
int ans=0;
for(int i=0;i<10000;i++){//只需枚举到10000,因为构造的回文串只有8位
string s=to_string(i);
string s3;
for(int j=s.size();j<4;j++){
s3+='0';
}
s3+=s;
string s4=s3;
reverse(s4.begin(),s4.end());//翻转,构造回文串
s4+=s3;
if(s4>=s1&&s4<=s2){
int c=stoi(s4.substr(0,4));//年
int d=stoi(s4.substr(4,2));//月
int e=stoi(s4.substr(6,2));//日
if(c%400==0||(c%4==0&&c%100!=0)){//如果是闰年,2月有29天
b[2]=29;
}
if(d>=1&&d<=12&&e>=1&&e<=b[d]){//如果枚举的回文是正确的日期,答案+1
ans++;
}
}
}
cout<<ans<<endl;
}
是不是很简单呢?
刚接触肯定会觉得难,多些做题多些用,熟悉了就容易了,兄弟萌,加油!!!
文章尚有不足,欢迎大牛们指正
感谢观看,点个赞吧
![[Square 2022] Hard Copy 复现](https://img-blog.csdnimg.cn/6cd71c6576b24c4081f6be6a84c88d3c.jpeg)