目录

0 本节关键词：栅格地图、算法、路径规划

1 Dijkstra算法详解

2 Dijkstra代码详解

---

0 本节关键词：栅格地图、算法、路径规划

1 Dijkstra算法详解

        用于图中寻找最短路径。节点是地点，边是权重。

        从起点开始逐步扩展，每一步为一个节点找到最短路径：

        While True:
                1.从未访问的节点选择距离最小的节点收录（贪心思想）
                2.收录节点后遍历该节点的邻接节点,更新距离

        我们举例子说明一下，在机器人路径规划中，通常用open list、closed list表达：

        open list 表示从该节点到起点已经有路径的节点

        closed list 表示已经找到最短路径的节点

        Step1：从起点开始，将起点放入open list中，选择距离最短的节点进行收录。

open list    1(0)(min)
closed list

|
|

open list    
closed list  1(0)

        Step2：遍历1号节点的邻接节点（4、2号节点）

open list    2(2)(1-->2) 4(1)(1-->4)(min)
closed list  1(0)

|
|

open list    2(2)(1-->2)
closed list  1(0)  4(1)(1-->4)

        4号节点收录后我们需要对其邻接节点更新距离。（3、6、7号节点）

        Step3：3号节点我们找到1->4->3路径，6号节点我们找到1->4->6路径，7号节点我们找到1->4->7路径。

open list    2(2)(1-->2)(min) 3(3)(1-->4-->3) 6(9)(1-->4-->6) 7(5)(1-->4-->7)
closed list  1(0)

|
|

open list    3(3)(1-->4-->3) 6(9)(1-->4-->6) 7(5)(1-->4-->7)
closed list  1(0)  4(1)(1-->4) 2(2)(1-->2)

        Step4：遍历2的邻接节点，我们发现4号节点已经在close list中（不需要被更新），我们更新5号节点。

open list    3(3)(1-->4-->3)(min) 6(9)(1-->4-->6) 7(5)(1-->4-->7) 5(13)(1->2-->5)
closed list  1(0)

|
|

open list    6(9)(1-->4-->6) 7(5)(1-->4-->7) 5(13)(1->2-->5)
closed list  1(0)  4(1)(1-->4) 2(2)(1-->2) 3(3)(1-->4-->3)

        Step5：遍历3的邻接节点，（3-->1无需更新，更新3-->6  1436(8) (因为我们有到3的最短距离)）,而我们已经为6号节点找到路径6(9)(146)，更新6号节点的路径。

open list    6(9)(1-->4-->6)(1->4->3-->6 7) 7(5)(1-->4-->7)(min) 5(13)(1->2-->5)
closed list  1(0)  4(1)(1-->4) 2(2)(1-->2) 3(3)(1-->4-->3)

|
|

open list    6(8)(1->4->3-->6) 5(13)(1->2-->5)
closed list  1(0)  4(1)(1-->4) 2(2)(1-->2) 3(3)(1-->4-->3) 7(5)(1-->4-->7)

        Step6：遍历7的邻接节点(6号节点)（1 4 7 6 = 6）比之前的8小，对6号距离再次更新。

open list    6(8)(1->4->3-->6)(1->4->7-->6 6)(min)  5(13)(1->2-->5) 
closed list  1(0)  4(1)(1-->4) 2(2)(1-->2) 3(3)(1-->4-->3) 7(5)(1-->4-->7) 

|
|

open list    5(13)(1->2-->5) 
closed list  1(0)  4(1)(1-->4) 2(2)(1-->2) 3(3)(1-->4-->3) 7(5)(1-->4-->7)  6(6)(1-->4-->7-->6)

        Step7：遍历6的邻接节点(6号节点)结束

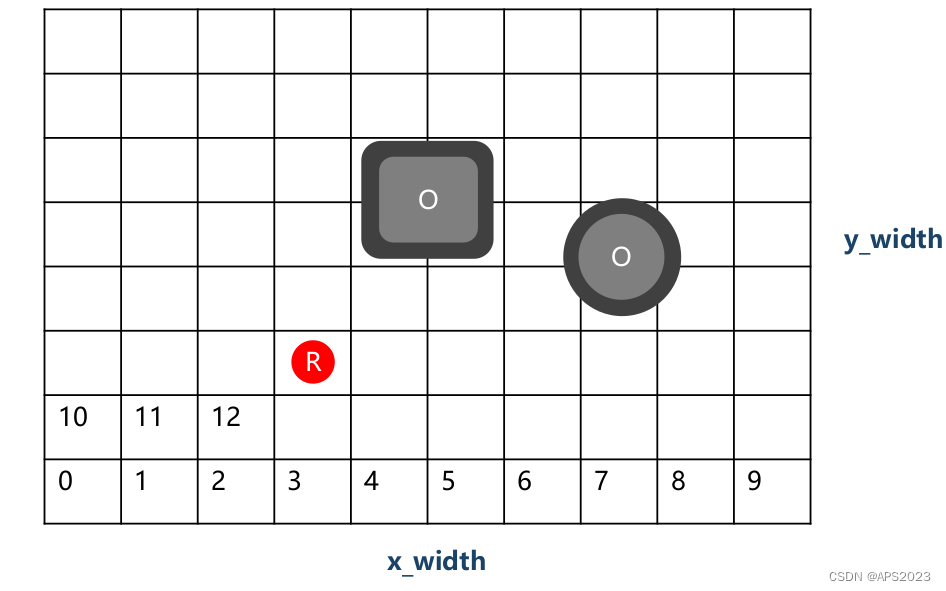
        栅格地图初介绍：

        假设图中灰色的是障碍物，红色的是机器人。在避障时，我们的常用做法是通过膨胀障碍物，将机器人视为质点来规划路径，然后对地图进行栅格化，将地图弄成一块一块的。最后将栅格地图转化为有权地图。我们可以把栅格地图的每个栅格看作是有权图的节点，机器人的运动范围可以看作是有权图的节点和节点之间的连接。

2 Dijkstra代码详解

        这里我们先配置下代码环境，最好是在python3.9下，我们创建conda虚拟环境：

conda create -n nav python=3.9

        安装所需库：

pip install numpy scipy matplotlib pandas cvxpy pytest -i https://pypi.tuna.tsinghua.edu.cn/simple

        我们的代码如下：

"""

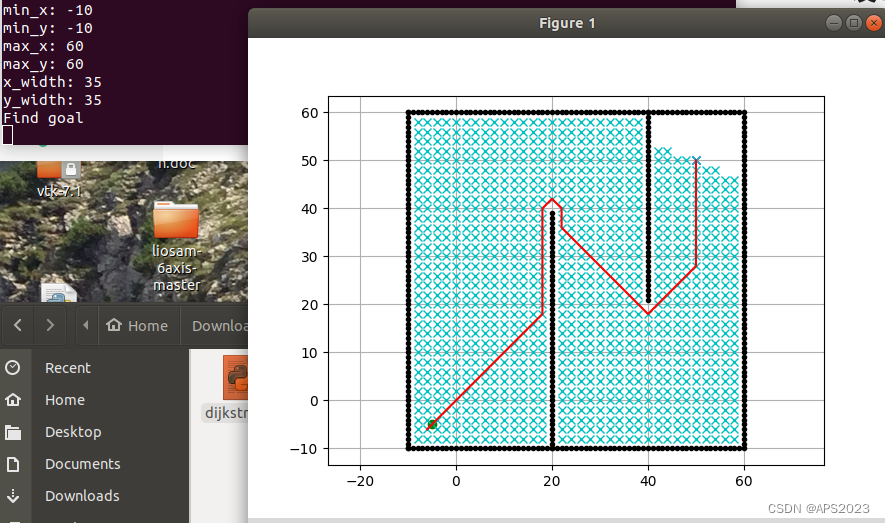
Grid based Dijkstra planning

author: Atsushi Sakai(@Atsushi_twi)

"""

import matplotlib.pyplot as plt
import math

show_animation = True


class Dijkstra:

    def __init__(self, ox, oy, resolution, robot_radius):
        """
        Initialize map for planning

        ox: x position list of Obstacles [m]
        oy: y position list of Obstacles [m]
        resolution: grid resolution [m]
        rr: robot radius[m]
        """

        self.min_x = None
        self.min_y = None
        self.max_x = None
        self.max_y = None
        self.x_width = None
        self.y_width = None
        self.obstacle_map = None

        self.resolution = resolution
        self.robot_radius = robot_radius
        self.calc_obstacle_map(ox, oy)
        self.motion = self.get_motion_model()

    class Node:
        def __init__(self, x, y, cost, parent_index):
            self.x = x  # index of grid
            self.y = y  # index of grid
            self.cost = cost  # g(n)
            self.parent_index = parent_index  # index of previous Node

        def __str__(self):
            return str(self.x) + "," + str(self.y) + "," + str(
                self.cost) + "," + str(self.parent_index)

    def planning(self, sx, sy, gx, gy):
        """
        dijkstra path search

        input:
            s_x: start x position [m]
            s_y: start y position [m]
            gx: goal x position [m]
            gx: goal x position [m]

        output:
            rx: x position list of the final path
            ry: y position list of the final path
        """

        start_node = self.Node(self.calc_xy_index(sx, self.min_x),
                               self.calc_xy_index(sy, self.min_y), 0.0, -1)   # round((position - minp) / self.resolution)
        goal_node = self.Node(self.calc_xy_index(gx, self.min_x),
                              self.calc_xy_index(gy, self.min_y), 0.0, -1)

        open_set, closed_set = dict(), dict()     # key - value: hash表
        open_set[self.calc_index(start_node)] = start_node

        while 1:
            c_id = min(open_set, key=lambda o: open_set[o].cost)  # 取cost最小的节点
            current = open_set[c_id]

            # show graph
            if show_animation:  # pragma: no cover
                plt.plot(self.calc_position(current.x, self.min_x),
                         self.calc_position(current.y, self.min_y), "xc")
                # for stopping simulation with the esc key.
                plt.gcf().canvas.mpl_connect(
                    'key_release_event',
                    lambda event: [exit(0) if event.key == 'escape' else None])
                if len(closed_set.keys()) % 10 == 0:
                    plt.pause(0.001)

            # 判断是否是终点
            if current.x == goal_node.x and current.y == goal_node.y:
                print("Find goal")
                goal_node.parent_index = current.parent_index
                goal_node.cost = current.cost
                break

            # Remove the item from the open set
            del open_set[c_id]

            # Add it to the closed set
            closed_set[c_id] = current

            # expand search grid based on motion model
            for move_x, move_y, move_cost in self.motion:
                node = self.Node(current.x + move_x,
                                 current.y + move_y,
                                 current.cost + move_cost, c_id)
                n_id = self.calc_index(node)

                if n_id in closed_set:
                    continue

                if not self.verify_node(node):
                    continue

                if n_id not in open_set:
                    open_set[n_id] = node  # Discover a new node
                else:
                    if open_set[n_id].cost >= node.cost:
                        # This path is the best until now. record it!
                        open_set[n_id] = node

        rx, ry = self.calc_final_path(goal_node, closed_set)

        return rx, ry

    def calc_final_path(self, goal_node, closed_set):
        # generate final course
        rx, ry = [self.calc_position(goal_node.x, self.min_x)], [
            self.calc_position(goal_node.y, self.min_y)]
        parent_index = goal_node.parent_index
        while parent_index != -1:
            n = closed_set[parent_index]
            rx.append(self.calc_position(n.x, self.min_x))
            ry.append(self.calc_position(n.y, self.min_y))
            parent_index = n.parent_index

        return rx, ry

    def calc_position(self, index, minp):
        pos = index * self.resolution + minp
        return pos

    def calc_xy_index(self, position, minp):
        return round((position - minp) / self.resolution)

    def calc_index(self, node):
        return node.y * self.x_width + node.x

    def verify_node(self, node):
        px = self.calc_position(node.x, self.min_x)
        py = self.calc_position(node.y, self.min_y)

        if px < self.min_x:
            return False
        if py < self.min_y:
            return False
        if px >= self.max_x:
            return False
        if py >= self.max_y:
            return False

        if self.obstacle_map[node.x][node.y]:
            return False

        return True

    def calc_obstacle_map(self, ox, oy):
        ''' 第1步：构建栅格地图 '''
        self.min_x = round(min(ox))
        self.min_y = round(min(oy))
        self.max_x = round(max(ox))
        self.max_y = round(max(oy))
        print("min_x:", self.min_x)
        print("min_y:", self.min_y)
        print("max_x:", self.max_x)
        print("max_y:", self.max_y)

        self.x_width = round((self.max_x - self.min_x) / self.resolution)
        self.y_width = round((self.max_y - self.min_y) / self.resolution)
        print("x_width:", self.x_width)
        print("y_width:", self.y_width)

        # obstacle map generation
        # 初始化地图
        self.obstacle_map = [[False for _ in range(self.y_width)]
                             for _ in range(self.x_width)]
        # 设置障碍物
        for ix in range(self.x_width):
            x = self.calc_position(ix, self.min_x)
            for iy in range(self.y_width):
                y = self.calc_position(iy, self.min_y)
                for iox, ioy in zip(ox, oy):
                    d = math.hypot(iox - x, ioy - y)
                    if d <= self.robot_radius:
                        self.obstacle_map[ix][iy] = True
                        break

    @staticmethod
    def get_motion_model():
        # dx, dy, cost
        motion = [[1, 0, 1],
                  [0, 1, 1],
                  [-1, 0, 1],
                  [0, -1, 1],
                  [-1, -1, math.sqrt(2)],
                  [-1, 1, math.sqrt(2)],
                  [1, -1, math.sqrt(2)],
                  [1, 1, math.sqrt(2)]]

        return motion

def main():
    # start and goal position
    sx = -5.0  # [m]
    sy = -5.0  # [m]
    gx = 50.0  # [m]
    gy = 50.0  # [m]
    grid_size = 2.0  # [m]
    robot_radius = 1.0  # [m]

    # set obstacle positions
    ox, oy = [], []
    for i in range(-10, 60):
        ox.append(i)
        oy.append(-10.0)
    for i in range(-10, 60):
        ox.append(60.0)
        oy.append(i)
    for i in range(-10, 61):
        ox.append(i)
        oy.append(60.0)
    for i in range(-10, 61):
        ox.append(-10.0)
        oy.append(i)
    for i in range(-10, 40):
        ox.append(20.0)
        oy.append(i)
    for i in range(0, 40):
        ox.append(40.0)
        oy.append(60.0 - i)

    if show_animation:  # pragma: no cover
        plt.plot(ox, oy, ".k")
        plt.plot(sx, sy, "og")
        plt.plot(gx, gy, "xb")
        plt.grid(True)
        plt.axis("equal")

    dijkstra = Dijkstra(ox, oy, grid_size, robot_radius)
    rx, ry = dijkstra.planning(sx, sy, gx, gy)

    if show_animation:  # pragma: no cover
        plt.plot(rx, ry, "-r")
        plt.pause(0.01)
        plt.show()

if __name__ == '__main__':
    main()

        先执行一下看看效果：

        我们现在来详解一下：

        我们从main函数开始：

    # 1. 设置起点和终点
    sx = -5.0  # [m]
    sy = -5.0  # [m]
    gx = 50.0  # [m]
    gy = 50.0  # [m]
    # 2. 设置珊格的大小和机器人的半径
    grid_size = 2.0  # [m]
    robot_radius = 1.0  # [m]

    # 3. 设置障碍物的位置（图中的黑点就是）
    ox, oy = [], []
    # 3.1 设置外围的四堵墙  (-10,-10)  --> (60,-10) 最下面的一条线
    for i in range(-10, 60):
        ox.append(i)
        oy.append(-10.0)
    # 3.1 设置外围的四堵墙  (60,-10)  -->  (60,60)  最右面的一条线
    for i in range(-10, 60):
        ox.append(60.0)
        oy.append(i)
    # 3.1 设置外围的四堵墙  (-10,60)  -->  (61,60)  最上面的一条线
    for i in range(-10, 61):
        ox.append(i)
        oy.append(60.0)
    # 3.1 设置外围的四堵墙  (-10,-10)  -->  (-10,61) 最左面的一条线
    for i in range(-10, 61):
        ox.append(-10.0)
        oy.append(i)

    # 3.2 障碍物
    for i in range(-10, 40):
        ox.append(20.0)
        oy.append(i)
    for i in range(0, 40):
        ox.append(40.0)
        oy.append(60.0 - i)

    # 4 画图 起点、终点、障碍物都画出来
    if show_animation:  # pragma: no cover
        plt.plot(ox, oy, ".k")
        plt.plot(sx, sy, "og")
        plt.plot(gx, gy, "xb")
        plt.grid(True)
        plt.axis("equal")

        这段代码就设置了边框和障碍物区域并把他们可视化了：

        就是我图中画的区域。

    #生成了Dijkstra的对象 调用其中的方法（障碍物信息、珊格大小、机器人半径）
    dijkstra = Dijkstra(ox, oy, grid_size, robot_radius)

        生成了Dijkstra的对象。我们来看这个类的构造函数，进入一个类首先执行构造函数：

    def __init__(self, ox, oy, resolution, robot_radius):
        """
        Initialize map for planning

        ox: x position list of Obstacles [m]
        oy: y position list of Obstacles [m]
        resolution: grid resolution [m]
        rr: robot radius[m]
        """

        self.min_x = None
        self.min_y = None
        self.max_x = None
        self.max_y = None
        self.x_width = None
        self.y_width = None
        self.obstacle_map = None

        # 珊格大小
        self.resolution = resolution
        # 机器人半径
        self.robot_radius = robot_radius
        # 构建珊格地图
        self.calc_obstacle_map(ox, oy)
        self.motion = self.get_motion_model()

        我们先来看是怎么创建珊格地图的：

    def calc_obstacle_map(self, ox, oy):
        ''' 第1步：构建栅格地图 '''

        # 1. 获得地图的边界值
        self.min_x = round(min(ox))
        self.min_y = round(min(oy))
        self.max_x = round(max(ox))
        self.max_y = round(max(oy))
        print("min_x:", self.min_x)
        print("min_y:", self.min_y)
        print("max_x:", self.max_x)
        print("max_y:", self.max_y)

        # 2.计算x、y方向珊格个数
        self.x_width = round((self.max_x - self.min_x) / self.resolution)
        self.y_width = round((self.max_y - self.min_y) / self.resolution)
        print("x_width:", self.x_width)
        print("y_width:", self.y_width)

        # obstacle map generation
        # 3.初始化地图 都设置为false 表示还没有设置障碍物
        self.obstacle_map = [[False for _ in range(self.y_width)]
                             for _ in range(self.x_width)]
        # 4.设置障碍物 遍历每一个栅格
        for ix in range(self.x_width):
            # 通过下标计算珊格位置
            x = self.calc_position(ix, self.min_x)
            for iy in range(self.y_width):
                y = self.calc_position(iy, self.min_y)
                # 遍历障碍物
                for iox, ioy in zip(ox, oy):
                    # 计算障碍物到珊格的距离
                    d = math.hypot(iox - x, ioy - y)
                    # 膨胀障碍物 如果距离比机器人半径小 机器人不能通行
                    if d <= self.robot_radius:
                        # 设置为true
                        self.obstacle_map[ix][iy] = True
                        break

        首先我们获得了地图的边界值，算出了每一个方向上有多少珊格数量。

        比如我们的长是100m（self.max_x - self.min_x = 100），珊格大小为3，那么我们每一行不就是有33个珊格啦～。

        我们初始化obstacle_map，这个大小为珊格长 * 珊格宽的大小，我们将他们初始化为false表示这个地方没有障碍物。

        然后我们遍历每一个珊格for ix in range(self.x_width)、for iy in range(self.y_width)。我们来看看calc_position这个方法做了什么。

    def calc_position(self, index, minp):
        pos = index * self.resolution + minp
        return pos

        其实就计算了珊格所在位置的真实(x,y)坐标，比如我们的self.minx = 10，ix = 0，那么他的pos = 0 * 2 + 10 = 10，比如我们的self.minx = 10，ix = 1，那么他的pos = 1 * 2 + 10 = 12。我们遍历所有障碍物体的坐标，计算障碍物体（真实坐标）与这个机器人的距离，如果这个距离比机器人自身的大小小的话，我们将这个地方的珊格标志置为false表示有东西。

        那么，在完成这个函数calc_obstacle_map时候，我们有了一张珊格地图，里面充斥着false和true，如果为true的话，那么机器人是过不去的，这块也就是设置成了障碍物区域。

        我们接着往下看构造函数：

        self.calc_obstacle_map(ox, oy)
        self.motion = self.get_motion_model()

         self.motion = self.get_motion_model()这段代码建立了机器人的运动模型和运动代价：

    def get_motion_model():
        # dx, dy, cost
        motion = [[1, 0, 1],                    #x增加1,y不变 代价为1
                  [0, 1, 1],
                  [-1, 0, 1],
                  [0, -1, 1],
                  [-1, -1, math.sqrt(2)],
                  [-1, 1, math.sqrt(2)],
                  [1, -1, math.sqrt(2)],
                  [1, 1, math.sqrt(2)]]

        return motion

        这里也就是机器人向左走(x+1,y+0)代价为1，斜着走代价为根号2。到此为止，我们构造函数讲解完了。我们返回主函数。

open_set

        这里开始正式进入路径规划了。传入的参数为起点坐标和终点坐标：

自动驾驶算法（一）：Dijkstra算法讲解与代码实现

        我们先看下node类。

    class Node:
        def __init__(self, x, y, cost, parent_index):
            self.x = x  # index of grid
            self.y = y  # index of grid
            self.cost = cost  # g(n)
            self.parent_index = parent_index  # index of previous Node

        def __str__(self):
            return str(self.x) + "," + str(self.y) + "," + str(
                self.cost) + "," + str(self.parent_index)

        首先执行构造函数，我们发现就是把珊格的(x,y)坐标（并非真实坐标是珊格的）还有cost（后文说）以及父节点的ID赋值了。（so easy）        

        我们在看一下calc_xy_index函数：

    def calc_xy_index(self, position, minp):
        return round((position - minp) / self.resolution)

        它就是计算出真实世界的点点属于哪一个珊格的某一维度的坐标，我们举个例子：

self.calc_xy_index(sx, self.min_x)  sx = 30  minx = 20

        这就代表我们的地图边界的 x 坐标为20，这个点的坐标x=30，我们用（30-20）/2 = 5，那么这个珊格坐标的x方向的坐标就是5。

        start_node = self.Node(self.calc_xy_index(sx, self.min_x),
                               self.calc_xy_index(sy, self.min_y), 0.0, -1)   # round((position - minp) / self.resolution)
        goal_node = self.Node(self.calc_xy_index(gx, self.min_x),
                              self.calc_xy_index(gy, self.min_y), 0.0, -1)

        因此，这段代码的含义就是我们计算出了起始和终止点的珊格坐标，并且将代价置为0，且他们的父节点为-1（没有父亲节点）。封装成了node。

        下面进入算法部分，我们看流程图：

        代码部分和流程图是一样的：

        1.首先我们把起点放入openlist中：

        # 设置openlist closelist 基于哈希表
        open_set, closed_set = dict(), dict()     # key - value: hash表
        # 将startnode放进openset里面 索引为一维数组
        open_set[self.calc_index(start_node)] = start_node

        看一下calc_index函数：这里将珊格地图映射成了一个一维数组，返回数组的ID，类似C++中的二维数组降维。这里openset是一个字典，里面的key是珊格地图点的ID，value是这个珊格节点。

    def calc_index(self, node):
        return node.y * self.x_width + node.x

        2.while True进入循环

        while 1:

        2.1 取openlist cost最小的节点作为当前节点

            c_id = min(open_set, key=lambda o: open_set[o].cost)
            current = open_set[c_id]

        2.2.1 判断当前是否为终点，如果是终点，如果是终点的话把终点的cost修改为当前点的cost值，且终点的父亲节点为当前点的父亲节点。

            # 判断是否是终点
            if current.x == goal_node.x and current.y == goal_node.y:
                print("Find goal")
                # 当前节点的信息赋值给终点
                goal_node.parent_index = current.parent_index
                goal_node.cost = current.cost
                break

        2.2.2 不是最终节点的话从openlist删除加入到closelist

            # 把当前节点从openset里面删掉
            del open_set[c_id]

            # 加入到closed set
            closed_set[c_id] = current

        2.3 遍历其9个邻接运动节点

            for move_x, move_y, move_cost in self.motion:

        2.3.1 封装邻接节点

node = self.Node(current.x + move_x,
                                 current.y + move_y,
                                 current.cost + move_cost, c_id)

        这个点到邻接节点的移动就是 x +-( 1或-1或+根号2或-根号2)，然后移动上下的话它的代价值需要+1，斜着移动需要 + 根号2，这样递归的进行我们就求出来所有点的代价值了，同样这个新走的点是通过我们这个点走过来的，因此新点的父节点就是我们这个点。

        2.3.2 求当前节点的一维索引判断是否收录到closelist并判断是否可行，如果收录了，那么已经有最小路径了不需要我们再去处理了，还需要判断这个节点是否在珊格地图标记为false点上（珊格地图就是这么用的....）如果这个地方有障碍物那么我们也走不了。

                # 求当前节点的key
                n_id = self.calc_index(node)

                # 是否已经收录到close set里面
                if n_id in closed_set:
                    continue

                # 邻接节点是否可行
                if not self.verify_node(node):
                    continue

        2.3.3 如果不在openset里面我们就将她作为一个新节点加入，如果在openset比较值是否是最优更新，是否和之前的最优路径有重叠。

                if n_id not in open_set:
                    open_set[n_id] = node  # Discover a new node
                else:
                    if open_set[n_id].cost >= node.cost:
                        # This path is the best until now. record it!
                        open_set[n_id] = node

        到这里我们的算法就结束了。我们迭代找到最终点后算法就break掉了～。

        最后我们计算路径：

    def calc_final_path(self, goal_node, closed_set):
        # generate final course
        rx, ry = [self.calc_position(goal_node.x, self.min_x)], [
            self.calc_position(goal_node.y, self.min_y)]
        parent_index = goal_node.parent_index
        while parent_index != -1:
            n = closed_set[parent_index]
            rx.append(self.calc_position(n.x, self.min_x))
            ry.append(self.calc_position(n.y, self.min_y))
            parent_index = n.parent_index

        return rx, ry

        我们将最终节点的珊格坐标还原成真实的三维坐标，并向前找他们的父亲节点直到起始节点（parent_index= -1），我们就出来这个路径了。