有意向获取代码，请转文末观看代码获取方式~

大家吃一顿火锅的价格便可以拥有13种信号分解+FFT傅里叶频谱变换联合算法，绝对不亏，知识付费是现今时代的趋势，而且都是我精心制作的教程，有问题可随时反馈~也可单独获取某一算法的代码（见每一算法介绍后文）~

1 【MATLAB】EMD 信号分解+FFT傅里叶频谱变换联合算法

EMD 是一种信号分解方法，它将一个信号分解成有限个本质模态函数 (EMD) 的和，每个 EMD 都是具有局部特征的振动模式。EMD 分解的主要步骤如下：

1. 将信号的局部极大值和极小值连接起来，形成一些局部极值包络线。

2. 对于每个局部极值包络线，通过线性插值得到一条平滑的包络线。然后将原信号减去该包络线，得到一条局部振荡的残差信号。

3. 对于该残差信号，重复步骤1和2，直到无法再分解出新的局部振荡模式为止。

4. 将所有的局部振荡模式相加，得到原始信号的EMD分解。 EMD分解的优点是能够很好地处理非线性和非平稳信号，并且不需要预先设定基函数。因此，EMD分解在信号处理、图像处理和模式识别等领域得到了广泛的应用。

原始数据分解各分量示意图

傅里叶变换是一种数学方法，用于将一个信号分解成一系列正弦和余弦函数的和，从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用，包括音频处理、图像处理等。 具体来说，傅里叶变换的步骤如下：

1. 给定一个连续时间域函数f(t)，其中t为时间。

2. 对f(t)进行傅里叶变换，得到它的频率域表示F(ω)，其中ω为角频率。

3. F(ω)表示了f(t)中所有频率分量的幅度和相位信息。

4. 将F(ω)分解成一系列正弦和余弦函数的和，即： F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中，k为频率分量的序号，a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号，从而更好地理解信号的频率分量和周期性特征，同时也方便进行一些信号处理任务，例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理，计算量较大，在实时处理等场景下可能会存在较大的延迟。

2【MATLAB】EEMD信号分解+FFT傅里叶频谱变换联合算法

EEMD是对EMD的改进，可以克服EMD的一些缺点。EEMD的主要思想是通过对原始数据集进行多次噪声扰动，获得多个EMD分解的集合，然后将这些EMD集合求平均，得到最终的EEMD分解结果。EEMD的主要步骤如下：

1. 对原始信号进行若干次随机噪声扰动，得到多个噪声扰动数据集。

2. 对每个噪声扰动数据集进行EMD分解，得到多个EMD分解集合。

3. 将每个 EMD 分解集合的对应分量进行平均，得到最终的 EEMD 分解结果。 EEMD 分解的优点是能够克服 EMD 的局限性，如基函数的选择和模态重叠等问题。同时，EEMD 还可以提供更好的信噪比和更高的分解精度。因此，EEMD 在信号处理、图像处理和模式识别等领域也得到了广泛的应用。

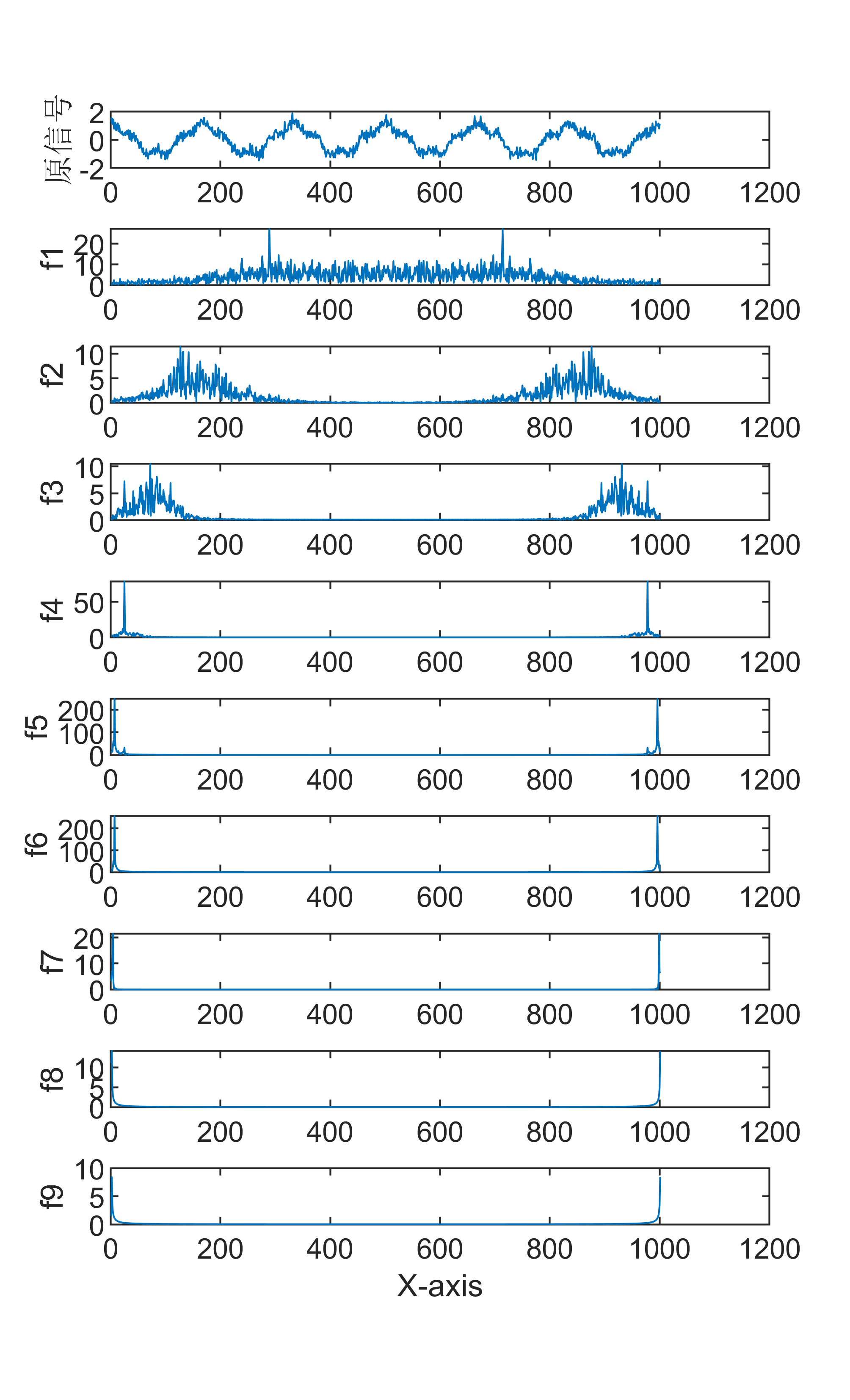
原始数据分解各分量示意图

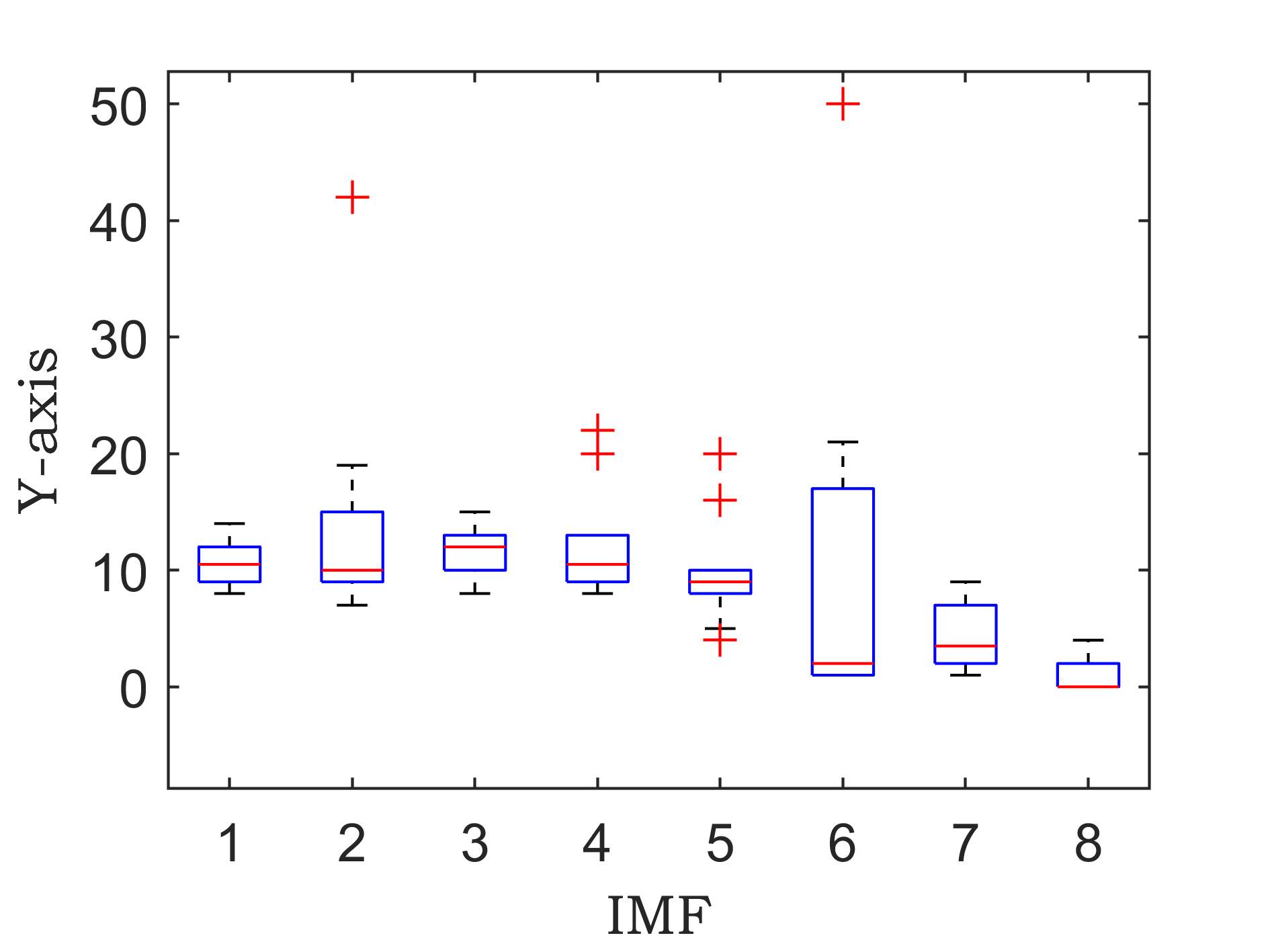
原始数据分解各分量的箱型图

傅里叶变换是一种数学方法，用于将一个信号分解成一系列正弦和余弦函数的和，从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用，包括音频处理、图像处理等。 具体来说，傅里叶变换的步骤如下：

1. 给定一个连续时间域函数f(t)，其中t为时间。

2. 对f(t)进行傅里叶变换，得到它的频率域表示F(ω)，其中ω为角频率。

3. F(ω)表示了f(t)中所有频率分量的幅度和相位信息。

4. 将F(ω)分解成一系列正弦和余弦函数的和，即： F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中，k为频率分量的序号，a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号，从而更好地理解信号的频率分量和周期性特征，同时也方便进行一些信号处理任务，例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理，计算量较大，在实时处理等场景下可能会存在较大的延迟。

3【MATLAB】CEEMD信号分解+FFT傅里叶频谱变换联合算法

CEEMD是对EEMD的改进，它在EEMD的基础上引入了一个自适应的扩展方法，可以更好地解决EMD/EEMD中存在的模态混叠问题。CEEMD的主要步骤如下：

1. 对原始信号进行若干次随机噪声扰动，得到多个噪声扰动数据集。

2. 对每个噪声扰动数据集进行EMD分解，得到多个EMD分解集合。

3. 对于每个EMD分解集合，通过一个自适应的扩展方法，将每个局部模态函数分配到它所属的固有模态函数上，消除模态混叠的影响。

4. 将每个扩展后的 EMD 分解集合的对应分量进行平均，得到最终的 CEEMD 分解结果。 CEEMD 分解具有良好的局部性和自适应性，能够更准确地分解信号，同时避免了 EEMD 中的模态混叠问题。因此，CEEMD 在信号处理、图像处理和模式识别等领域也得到了广泛的应用。

原始数据分解各分量示意图

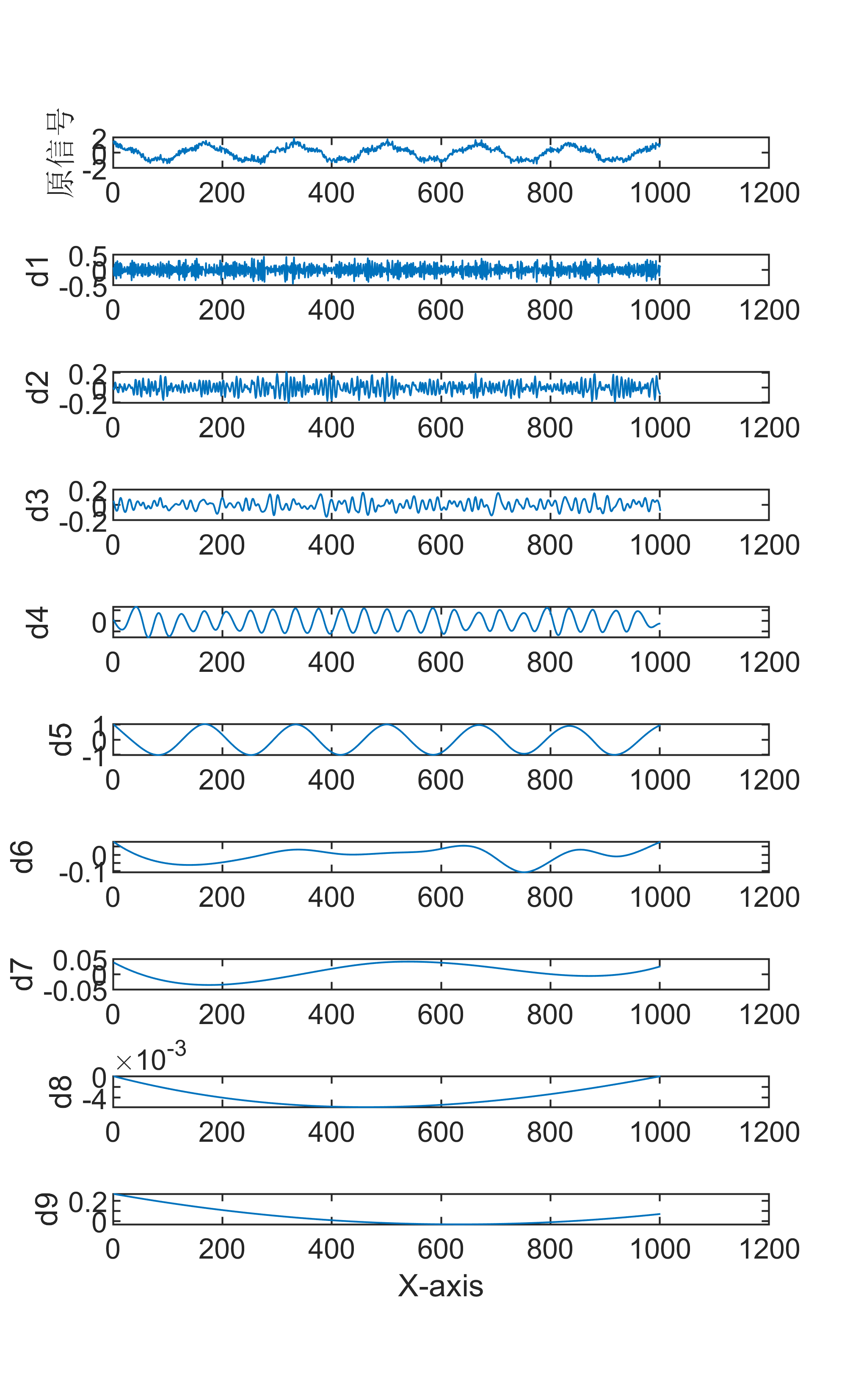
傅里叶变换是一种数学方法，用于将一个信号分解成一系列正弦和余弦函数的和，从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用，包括音频处理、图像处理等。 具体来说，傅里叶变换的步骤如下：

1. 给定一个连续时间域函数f(t)，其中t为时间。

2. 对f(t)进行傅里叶变换，得到它的频率域表示F(ω)，其中ω为角频率。

3. F(ω)表示了f(t)中所有频率分量的幅度和相位信息。

4. 将F(ω)分解成一系列正弦和余弦函数的和，即： F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中，k为频率分量的序号，a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号，从而更好地理解信号的频率分量和周期性特征，同时也方便进行一些信号处理任务，例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理，计算量较大，在实时处理等场景下可能会存在较大的延迟。

4【MATLAB】CEEMDAN信号分解+FFT傅里叶频谱变换联合算法

CEEMDAN是对CEEMD的进一步改进，它引入了一种自适应噪声辅助方法，可以更好地处理信号中的高频噪声。CEEMDAN的主要步骤如下：

1. 对原始信号进行若干次随机噪声扰动，得到多个噪声扰动数据集。

2. 对每个噪声扰动数据集进行CEEMD分解，得到多个CEEMD分解集合。

3. 对于每个CEEMD分解集合，引入自适应噪声辅助方法，通过将噪声信号添加到每个局部模态函数中，增强信号的边缘和高频部分。

4. 将每个自适应噪声辅助后的 CEEMD 分解集合的对应分量进行平均，得到最终的 CEEMDAN 分解结果。 CEEMDAN 分解具有更好的对高频噪声的适应性，能够更准确地分解信号。因此，CEEMDAN 在信号处理、图像处理和模式识别等领域也得到了广泛的应用。

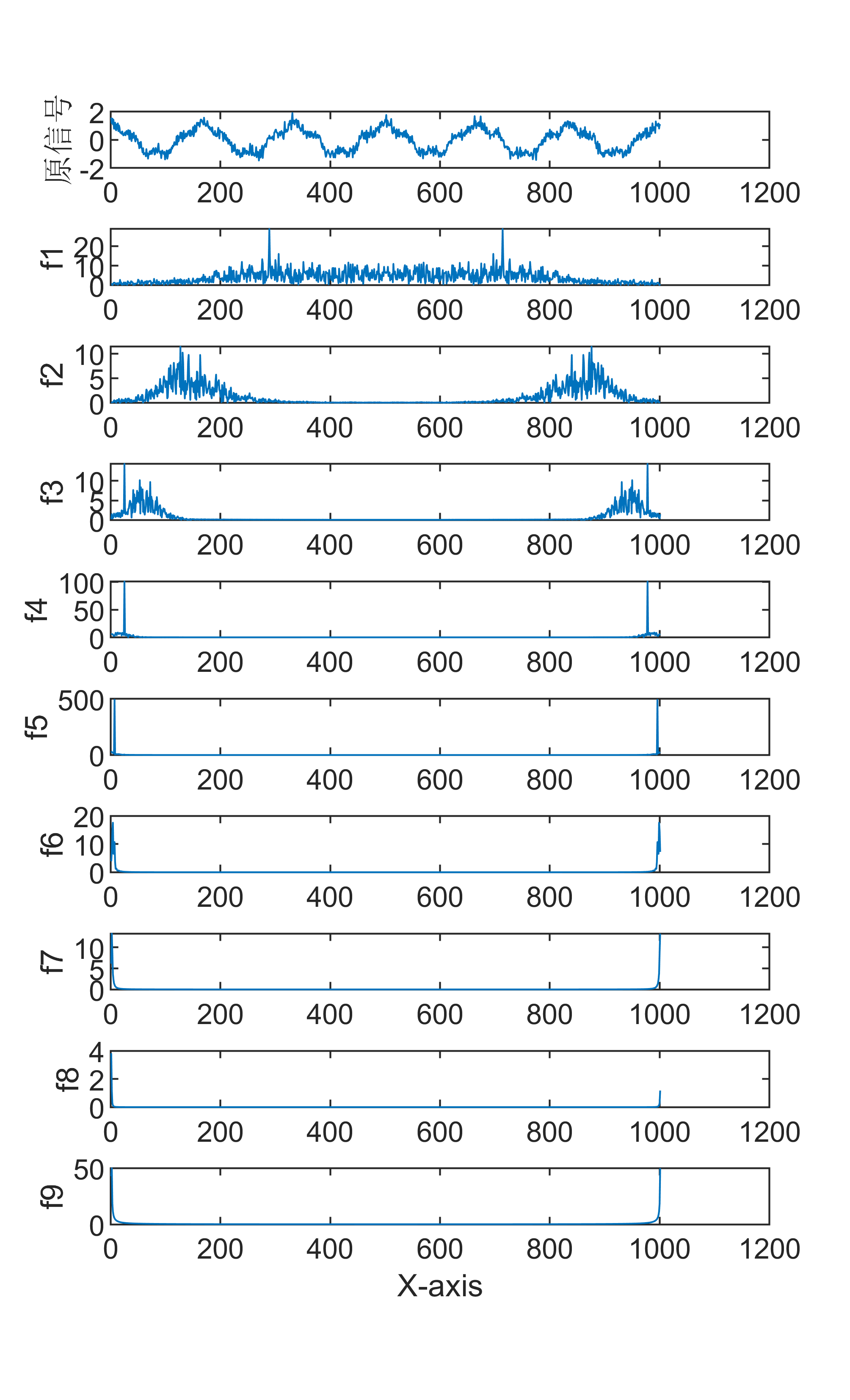
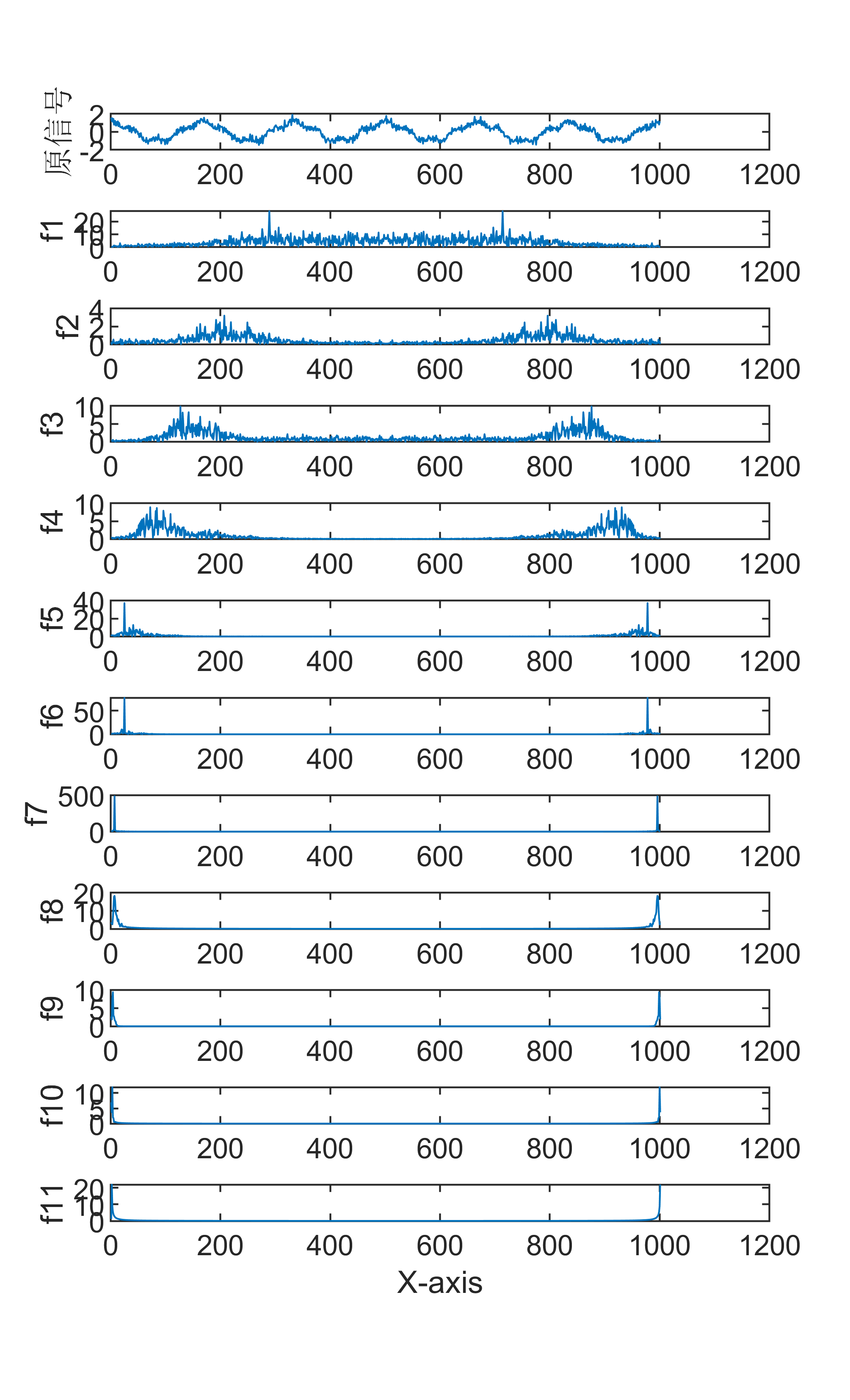
原始数据分解各分量示意图

原始数据分解各分量的箱型图

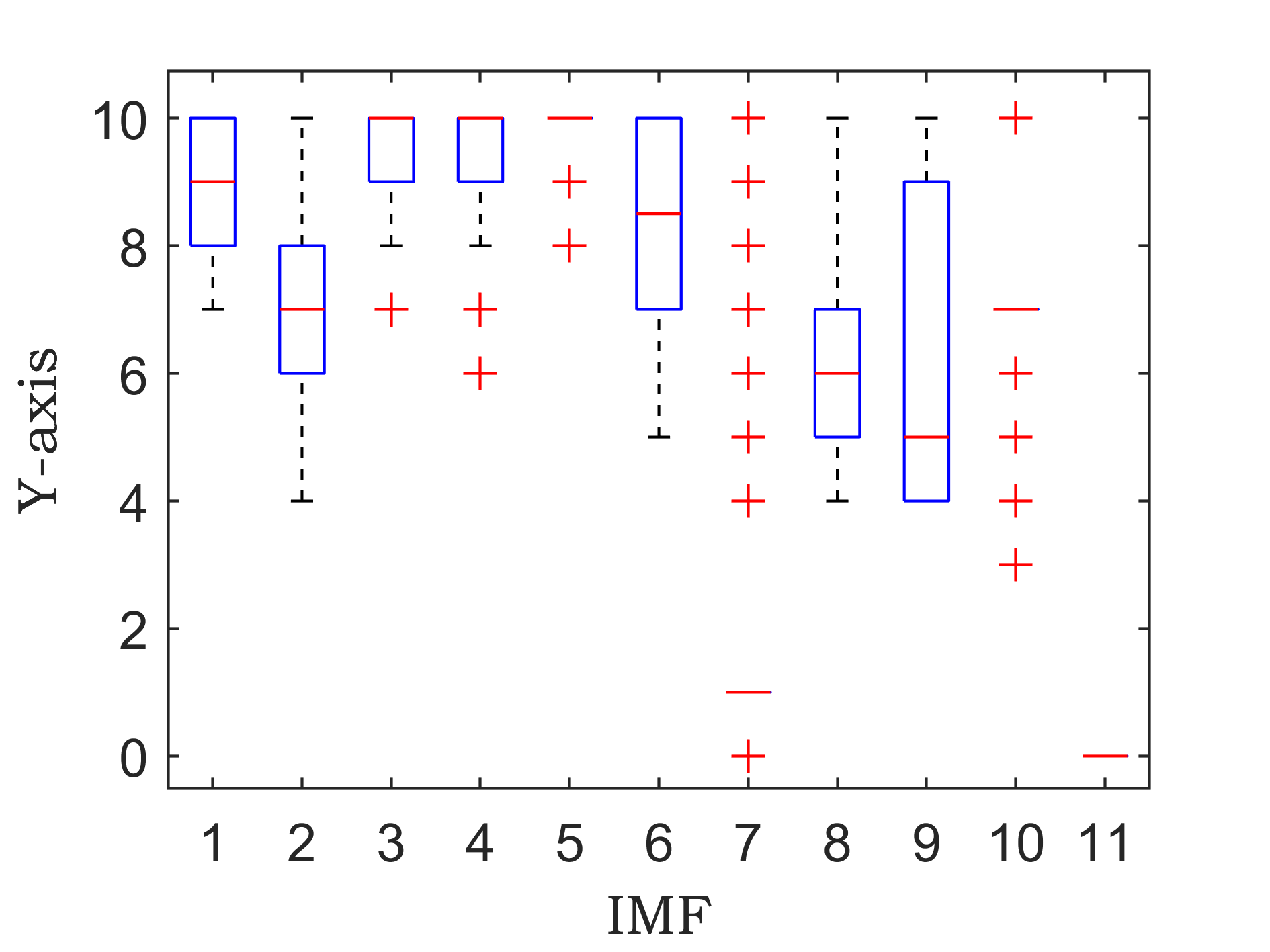
傅里叶变换是一种数学方法，用于将一个信号分解成一系列正弦和余弦函数的和，从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用，包括音频处理、图像处理等。 具体来说，傅里叶变换的步骤如下：

1. 给定一个连续时间域函数f(t)，其中t为时间。

2. 对f(t)进行傅里叶变换，得到它的频率域表示F(ω)，其中ω为角频率。

3. F(ω)表示了f(t)中所有频率分量的幅度和相位信息。

4. 将F(ω)分解成一系列正弦和余弦函数的和，即： F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中，k为频率分量的序号，a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号，从而更好地理解信号的频率分量和周期性特征，同时也方便进行一些信号处理任务，例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理，计算量较大，在实时处理等场景下可能会存在较大的延迟。

5【MATLAB】ICEEMDAN信号分解+FFT傅里叶频谱变换联合算法

ICEEMDAN (Improved Complete Ensemble EMD with Adaptive Noise) 是一种基于经验模态分解（Empirical Mode Decomposition, EMD）的信号分解方法。与传统的 EMD 方法不同，ICEEMDAN 引入了自适应噪声和完整集成策略，以提高分解的稳定性和准确性。在 ICEEMDAN 方法中，首先采用 EMD 将原始信号分解成多个固有模态函数（Intrinsic Mode Functions, IMF），然后通过自适应噪声算法去除每个 IMF 中的噪声，最后将去噪后的 IMFs 进行完整集成，得到分解后的信号。相比于传统的 EMD 方法，ICEEMDAN 采用自适应噪声算法去除噪声，可以减少分解过程中的模态混叠问题。此外，完整集成策略可以保证分解后的信号保留了原始信号的全部信息，提高了分解的准确性。 ICEEMDAN 分解方法在信号处理、图像处理、语音处理等领域得到了广泛应用，具有较高的分解效果和可靠性。

原始数据分解各分量示意图

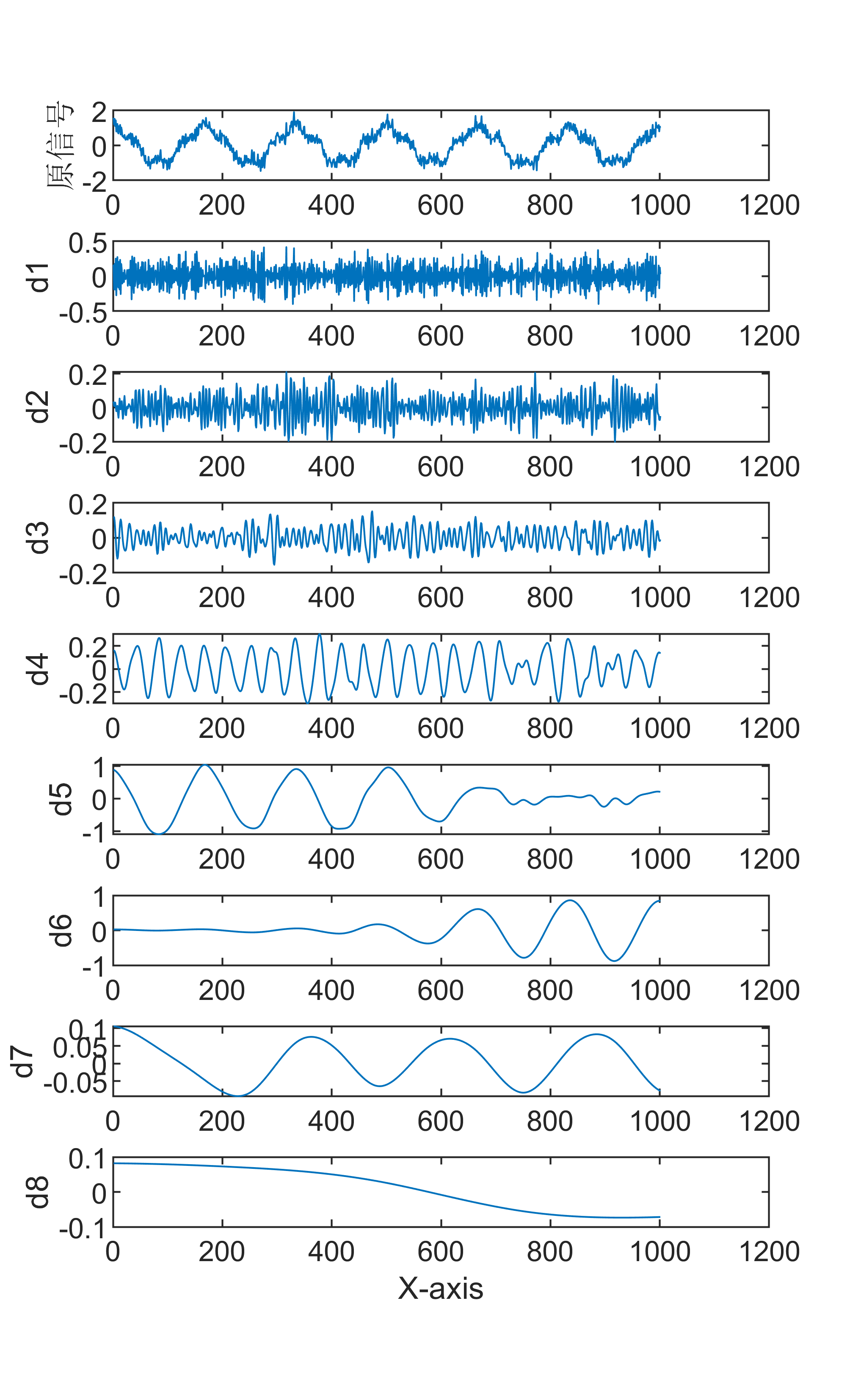
傅里叶变换是一种数学方法，用于将一个信号分解成一系列正弦和余弦函数的和，从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用，包括音频处理、图像处理等。 具体来说，傅里叶变换的步骤如下：

1. 给定一个连续时间域函数f(t)，其中t为时间。

2. 对f(t)进行傅里叶变换，得到它的频率域表示F(ω)，其中ω为角频率。

3. F(ω)表示了f(t)中所有频率分量的幅度和相位信息。

4. 将F(ω)分解成一系列正弦和余弦函数的和，即： F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中，k为频率分量的序号，a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号，从而更好地理解信号的频率分量和周期性特征，同时也方便进行一些信号处理任务，例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理，计算量较大，在实时处理等场景下可能会存在较大的延迟。

6【MATLAB】小波分解信号分解+FFT傅里叶频谱变换联合算法

小波分解算法是一种数学方法，用于将信号分解为不同频率的小波成分。这种算法基于小波函数，可以用于信号处理、图像压缩和数据压缩等领域。小波分解算法的基本思想是将一个信号分解成多个小波子带，每个小波子带代表了一个不同频率的小波成分。这些小波子带可以分别进行处理，例如滤波、降采样等操作，然后再进行重构，得到原始信号。小波分解算法的优点是可以提供更好的时频分辨率，对于瞬态信号和非平稳信号的处理效果更好。同时，小波分解算法也可以用于图像压缩和数据压缩，因为小波分解后的子带可以选择性地保留或舍弃，从而实现数据压缩。总之，小波分解算法是一种强大的信号处理技术，被广泛应用于信号处理、图像压缩和数据压缩等领域。

原始数据分解各分量示意图

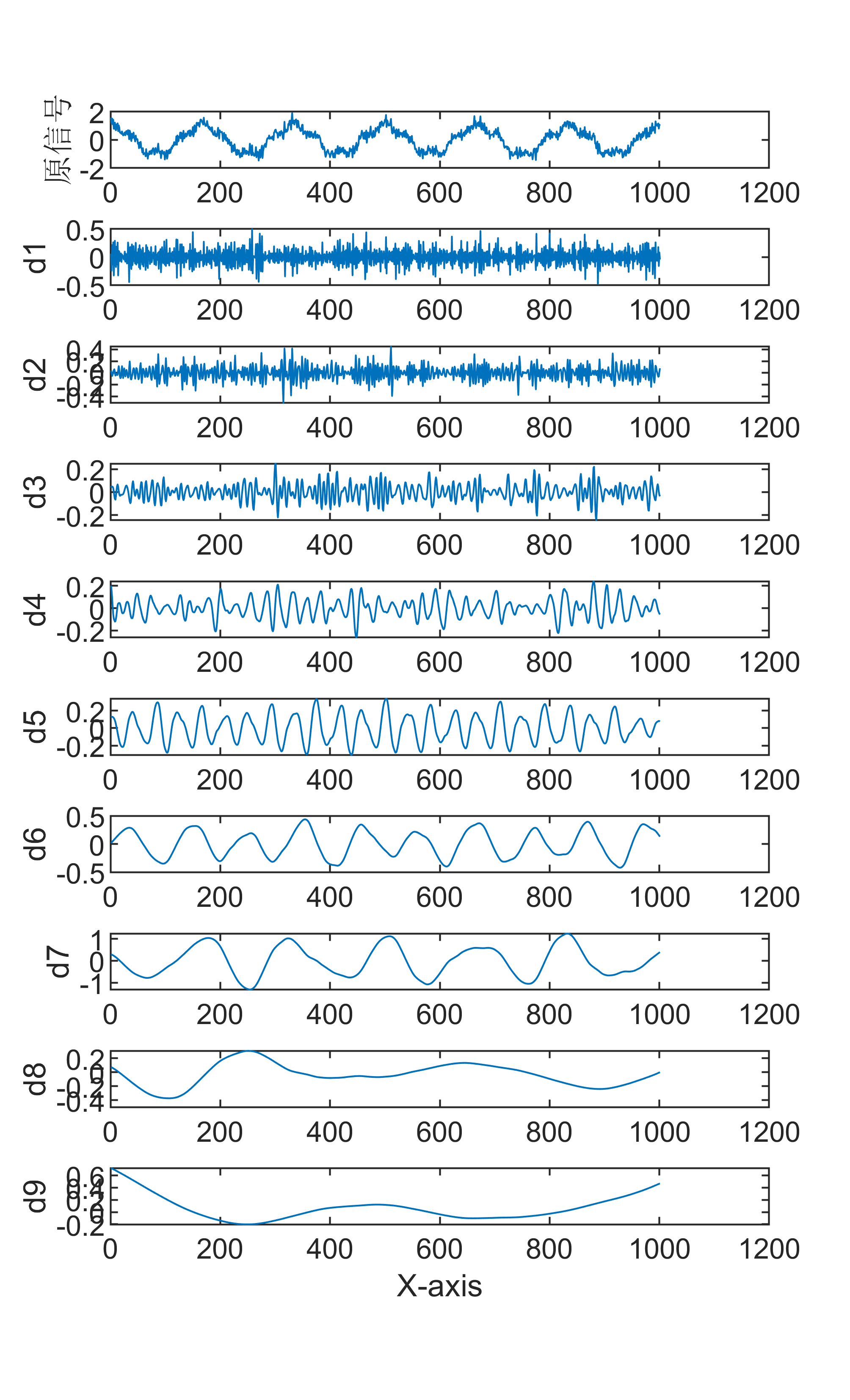
傅里叶变换是一种数学方法，用于将一个信号分解成一系列正弦和余弦函数的和，从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用，包括音频处理、图像处理等。 具体来说，傅里叶变换的步骤如下：

1. 给定一个连续时间域函数f(t)，其中t为时间。

2. 对f(t)进行傅里叶变换，得到它的频率域表示F(ω)，其中ω为角频率。

3. F(ω)表示了f(t)中所有频率分量的幅度和相位信息。

4. 将F(ω)分解成一系列正弦和余弦函数的和，即： F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中，k为频率分量的序号，a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号，从而更好地理解信号的频率分量和周期性特征，同时也方便进行一些信号处理任务，例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理，计算量较大，在实时处理等场景下可能会存在较大的延迟。

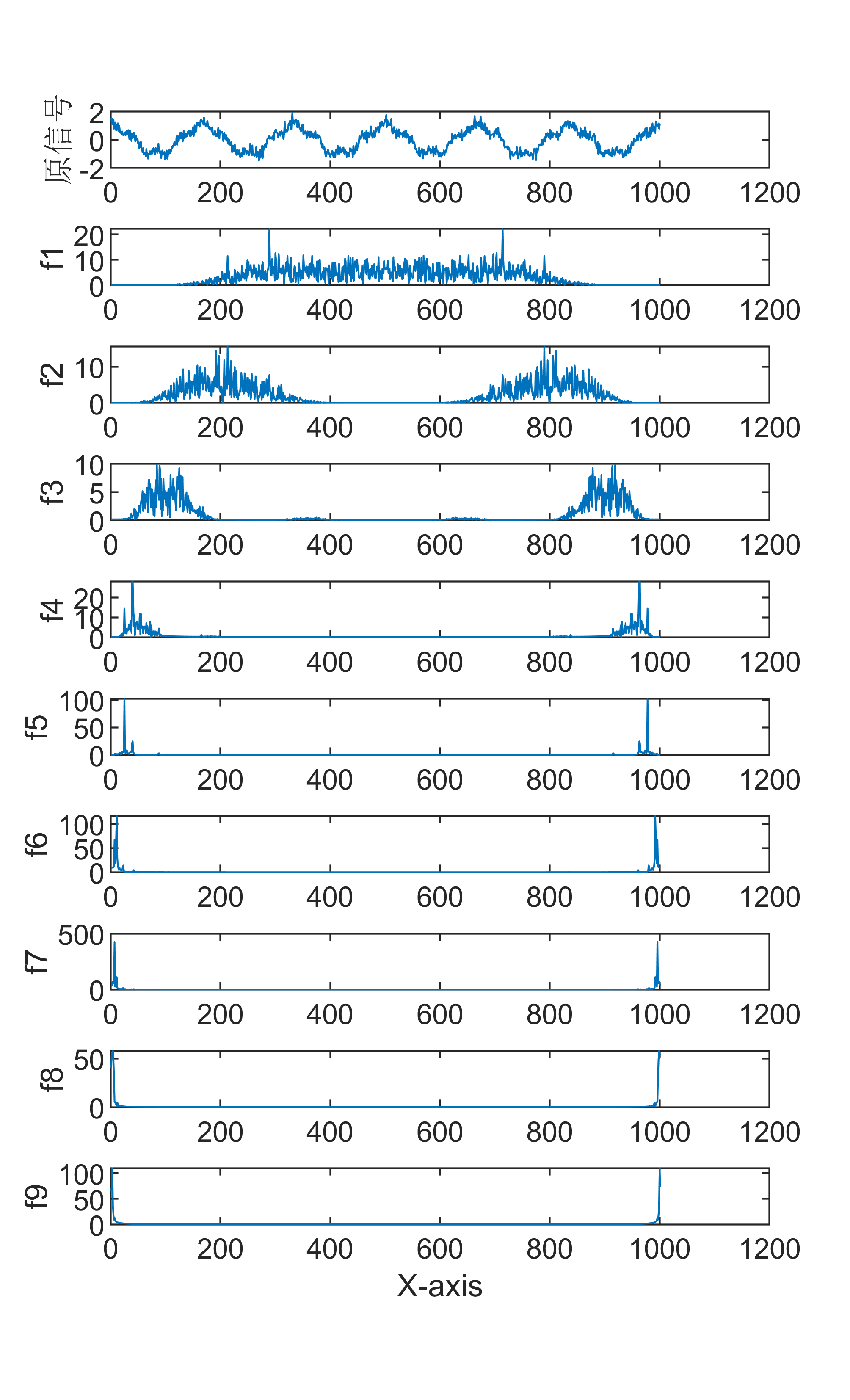
7【MATLAB】VMD信号分解+FFT傅里叶频谱变换联合算法

VMD是一种新型的信号分解方法，它是通过使用变分推断方法将信号分解为一组局部振动模式，每个模式包含多个频率组件。VMD的主要步骤如下：

1. 将原始信号进行多次低通滤波，得到多个频带信号。

2. 对每个频带信号进行变分推断，得到该频带信号的局部振动模式。

3. 将所有频带信号对应的局部振动模式相加，得到原始信号的 VMD 分解。 VMD 分解具有以下优点：能够自动提取信号的局部特征，避免了传统分解方法中需要手动选择基函数的问题；能够处理非线性和非平稳信号，并且不会产生模态重叠的问题。因此，VMD 在信号处理、图像处理和模式识别等领域也得到了广泛的应用。

原始数据分解各分量示意图

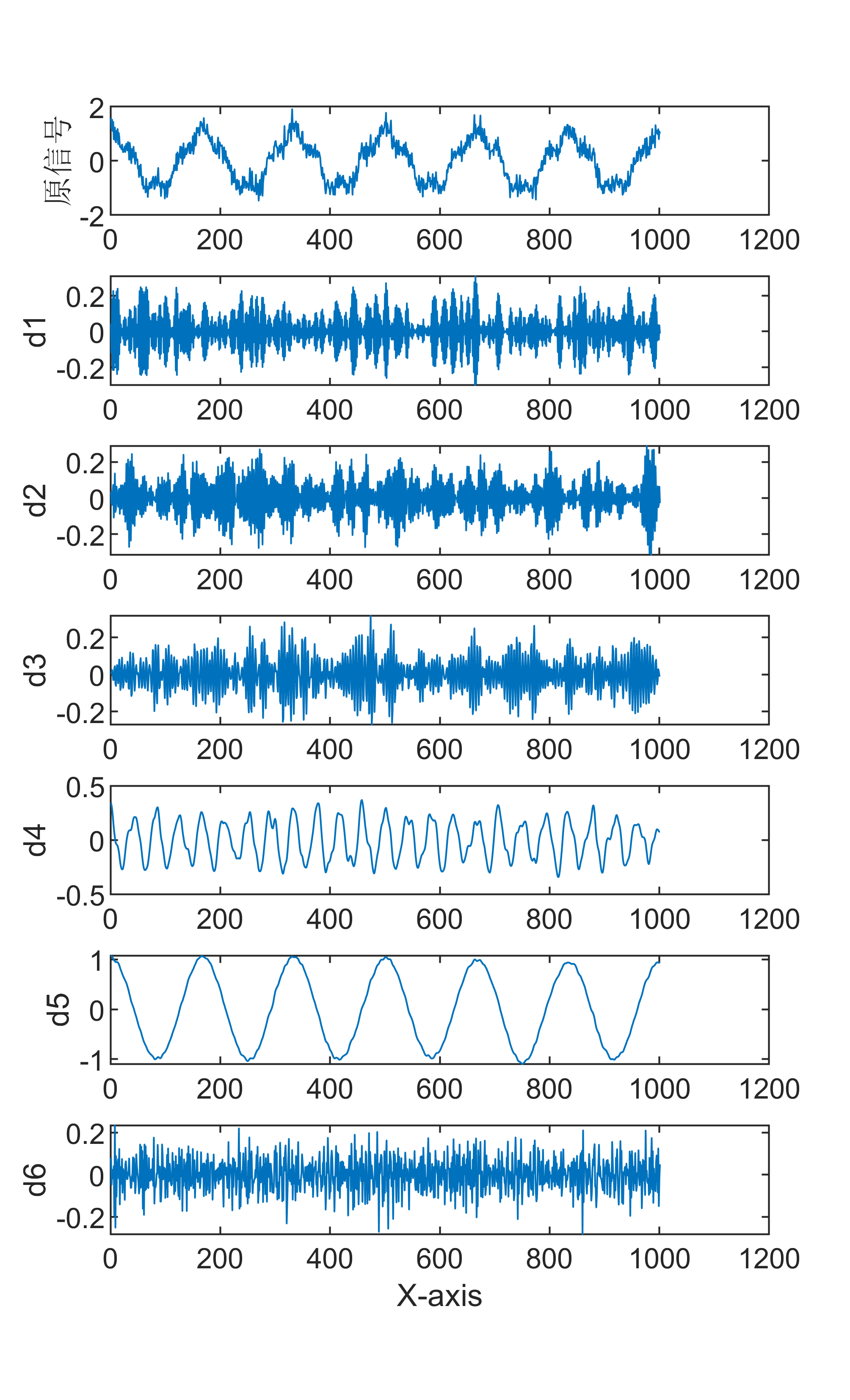
傅里叶变换是一种数学方法，用于将一个信号分解成一系列正弦和余弦函数的和，从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用，包括音频处理、图像处理等。 具体来说，傅里叶变换的步骤如下：

1. 给定一个连续时间域函数f(t)，其中t为时间。

2. 对f(t)进行傅里叶变换，得到它的频率域表示F(ω)，其中ω为角频率。

3. F(ω)表示了f(t)中所有频率分量的幅度和相位信息。

4. 将F(ω)分解成一系列正弦和余弦函数的和，即： F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中，k为频率分量的序号，a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号，从而更好地理解信号的频率分量和周期性特征，同时也方便进行一些信号处理任务，例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理，计算量较大，在实时处理等场景下可能会存在较大的延迟。

8【MATLAB】LMD信号分解+FFT傅里叶频谱变换联合算法

LMD (Local Mean Decomposition) 分解算法是一种信号分解算法，它可以将一个信号分解成多个局部平滑的成分，并且可以将高频噪声和低频信号有效地分离出来。LMD 分解算法是一种自适应的分解方法，可以根据信号的局部特征来进行分解，从而提高了分解的精度和效果。 LMD 分解算法的基本思想是，在原始信号中选取局部的极大值点和极小值点，然后通过这些极值点之间的平均值来计算一个局部平滑的成分。这个过程可以迭代进行，直到得到所有的局部平滑的成分。最后，将这些局部平滑的成分加起来，即可得到原始信号的分解结果。 LMD 分解算法具有以下优点：

1. 自适应性强：LMD 分解算法可以根据信号的局部特征来进行分解，从而提高了分解的精度和效果。

2. 分解精度高：LMD 分解算法可以将高频噪声和低频信号有效地分离出来，从而提高了分解的精度。

3. 计算效率高：LMD 分解算法的计算量较小，可以快速地进行信号分解。总之，LMD 分解算法是一种高效、精确、自适应的信号分解算法，被广泛应用于信号处理、图像处理、语音处理等领域。

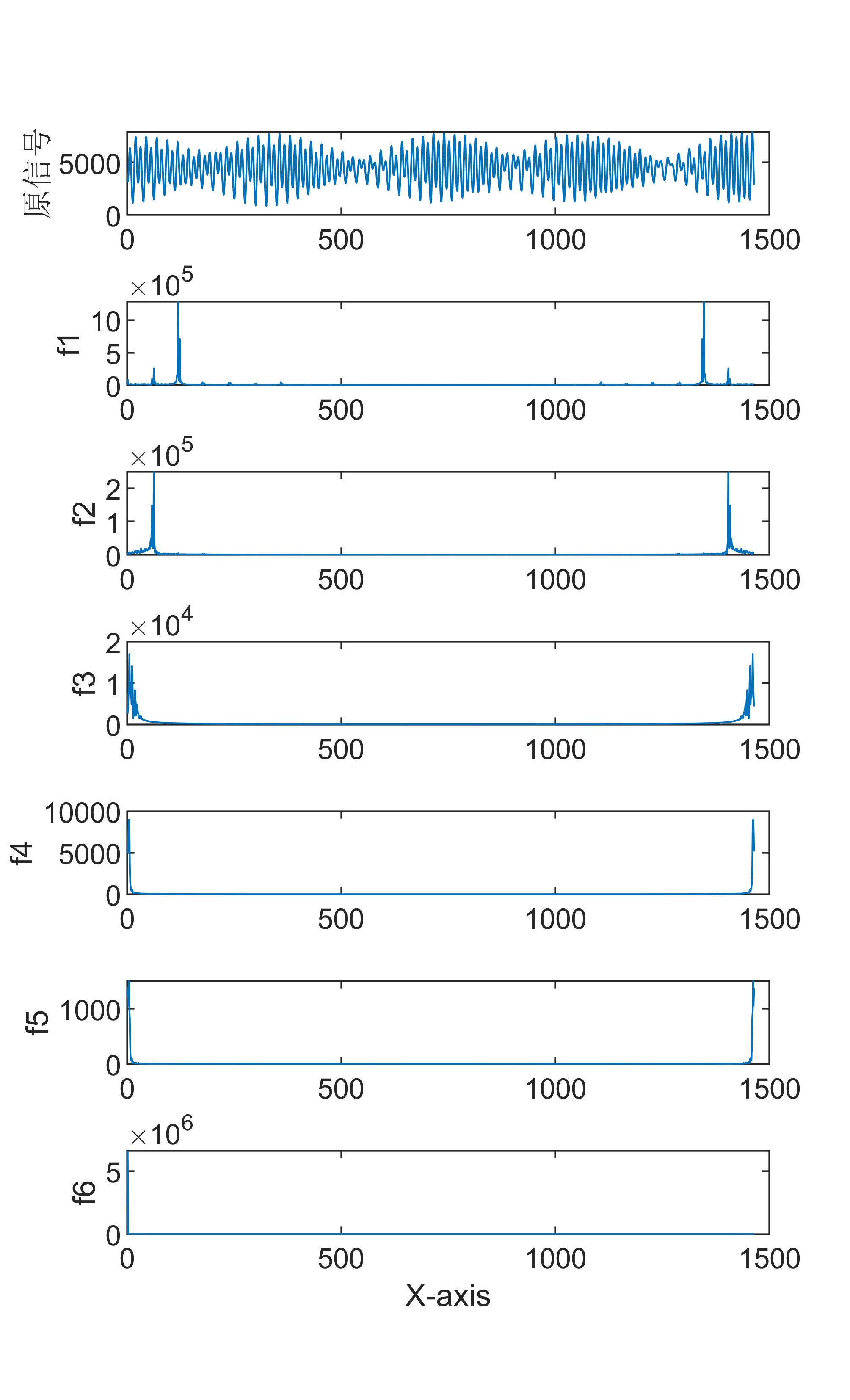
原始数据分解各分量示意图

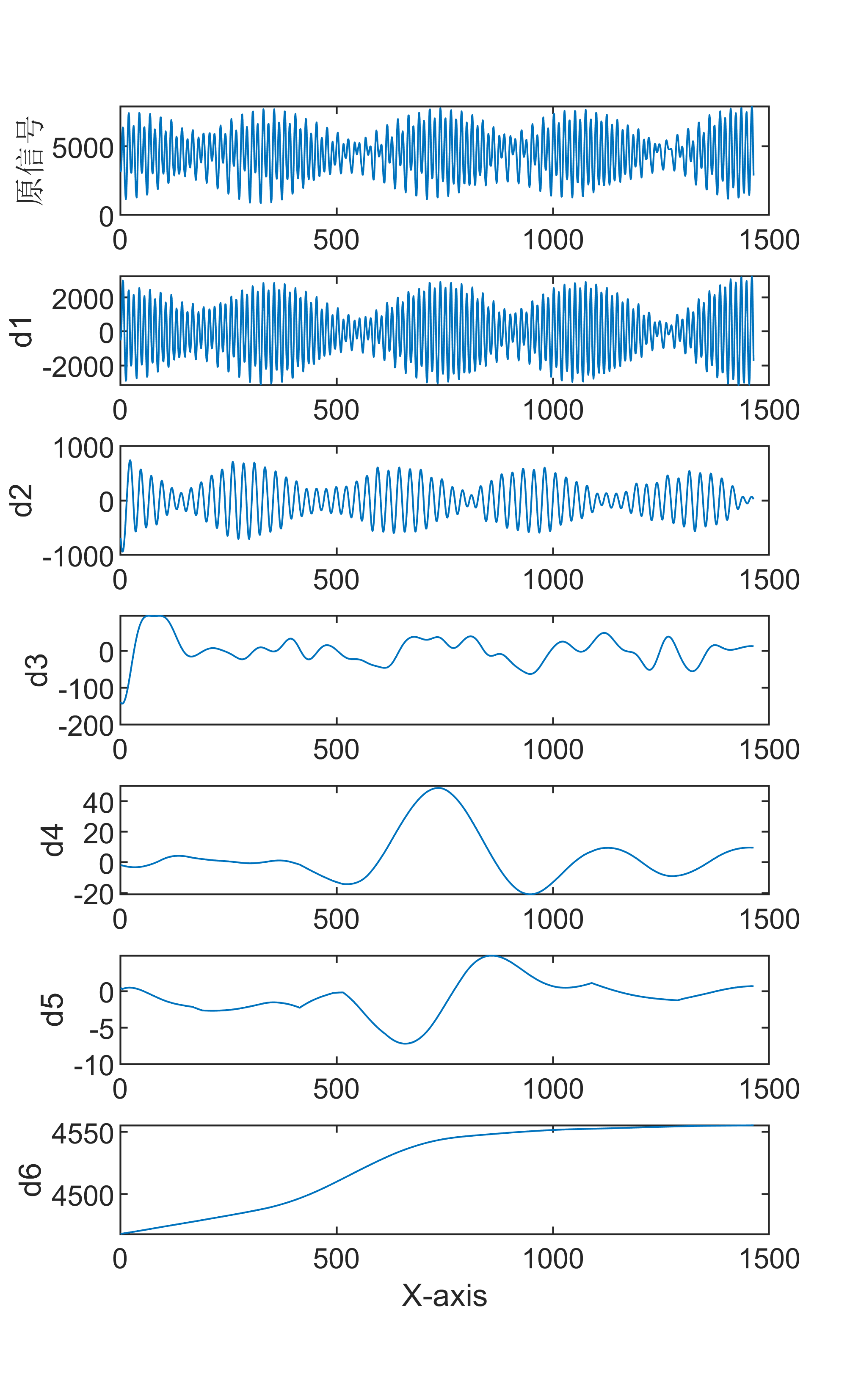
傅里叶变换是一种数学方法，用于将一个信号分解成一系列正弦和余弦函数的和，从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用，包括音频处理、图像处理等。 具体来说，傅里叶变换的步骤如下：

1. 给定一个连续时间域函数f(t)，其中t为时间。

2. 对f(t)进行傅里叶变换，得到它的频率域表示F(ω)，其中ω为角频率。

3. F(ω)表示了f(t)中所有频率分量的幅度和相位信息。

4. 将F(ω)分解成一系列正弦和余弦函数的和，即： F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中，k为频率分量的序号，a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号，从而更好地理解信号的频率分量和周期性特征，同时也方便进行一些信号处理任务，例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理，计算量较大，在实时处理等场景下可能会存在较大的延迟。

9【MATLAB】RLMD信号分解+FFT傅里叶频谱变换联合算法

RLMD（Robust Local Mode Decomposition）是一种鲁棒的局部模态分解方法。它是通过在局部区间内对信号进行多项式拟合，提取局部特征，进而分解信号为多个局部模态函数的和。RLMD的主要步骤如下：

1. 将原始信号分段，对每个局部区间内的信号进行多项式拟合，得到该局部区间的局部趋势。

2. 将原始信号减去该局部区间的局部趋势，得到该局部区间内的局部振动模式。

3. 对每个局部振动模式，重复步骤1和2，直到该局部振动模式变为平稳信号，得到该局部区间内的局部模态函数。

4. 将所有局部区间内的局部模态函数相加，得到原始信号的 RLMD 分解。 RLMD 分解具有对噪声和异常值的鲁棒性，能够更准确地分解信号。同时，RLMD 还能够处理非平稳信号，具有较好的局部性和自适应性。因此，RLMD 在信号处理、图像处理和模式识别等领域也得到了广泛的应用。

原始数据分解各分量示意图

傅里叶变换是一种数学方法，用于将一个信号分解成一系列正弦和余弦函数的和，从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用，包括音频处理、图像处理等。 具体来说，傅里叶变换的步骤如下：

1. 给定一个连续时间域函数f(t)，其中t为时间。

2. 对f(t)进行傅里叶变换，得到它的频率域表示F(ω)，其中ω为角频率。

3. F(ω)表示了f(t)中所有频率分量的幅度和相位信息。

4. 将F(ω)分解成一系列正弦和余弦函数的和，即： F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中，k为频率分量的序号，a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号，从而更好地理解信号的频率分量和周期性特征，同时也方便进行一些信号处理任务，例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理，计算量较大，在实时处理等场景下可能会存在较大的延迟。

10【MATLAB】EWT 信号分解+FFT傅里叶频谱变换联合算法

EWT (Empirical Wavelet Transform) 分解算法是一种用于信号分解的方法，它可以将信号分解成多个局部频率的小波成分，从而实现对信号的高效处理和分析。EWT 分解算法基于小波分析和自适应滤波器，可以适应不同类型的信号，并且能够处理非平稳信号和非线性信号。 EWT 分解算法的基本思想是，首先将信号分解成多个局部频率的小波成分，然后通过自适应滤波器对每个小波成分进行去噪和平滑处理，最后将处理后的小波成分合并起来得到原始信号的分解结果。 EWT 分解算法具有以下优点：

1. 适应性强：EWT 分解算法可以适应不同类型的信号，并且能够处理非平稳信号和非线性信号。

2. 分解精度高：EWT 分解算法可以将信号分解成多个局部频率的小波成分，从而提高了分解的精度。

3. 计算效率高：EWT 分解算法的计算量较小，可以快速地进行信号分解。总之，EWT 分解算法是一种高效、精确、适应性强的信号分解算法，被广泛应用于信号处理、图像处理、语音处理等领域。

原始数据分解各分量示意图

傅里叶变换是一种数学方法，用于将一个信号分解成一系列正弦和余弦函数的和，从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用，包括音频处理、图像处理等。 具体来说，傅里叶变换的步骤如下：

1. 给定一个连续时间域函数f(t)，其中t为时间。

2. 对f(t)进行傅里叶变换，得到它的频率域表示F(ω)，其中ω为角频率。

3. F(ω)表示了f(t)中所有频率分量的幅度和相位信息。

4. 将F(ω)分解成一系列正弦和余弦函数的和，即： F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中，k为频率分量的序号，a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号，从而更好地理解信号的频率分量和周期性特征，同时也方便进行一些信号处理任务，例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理，计算量较大，在实时处理等场景下可能会存在较大的延迟。

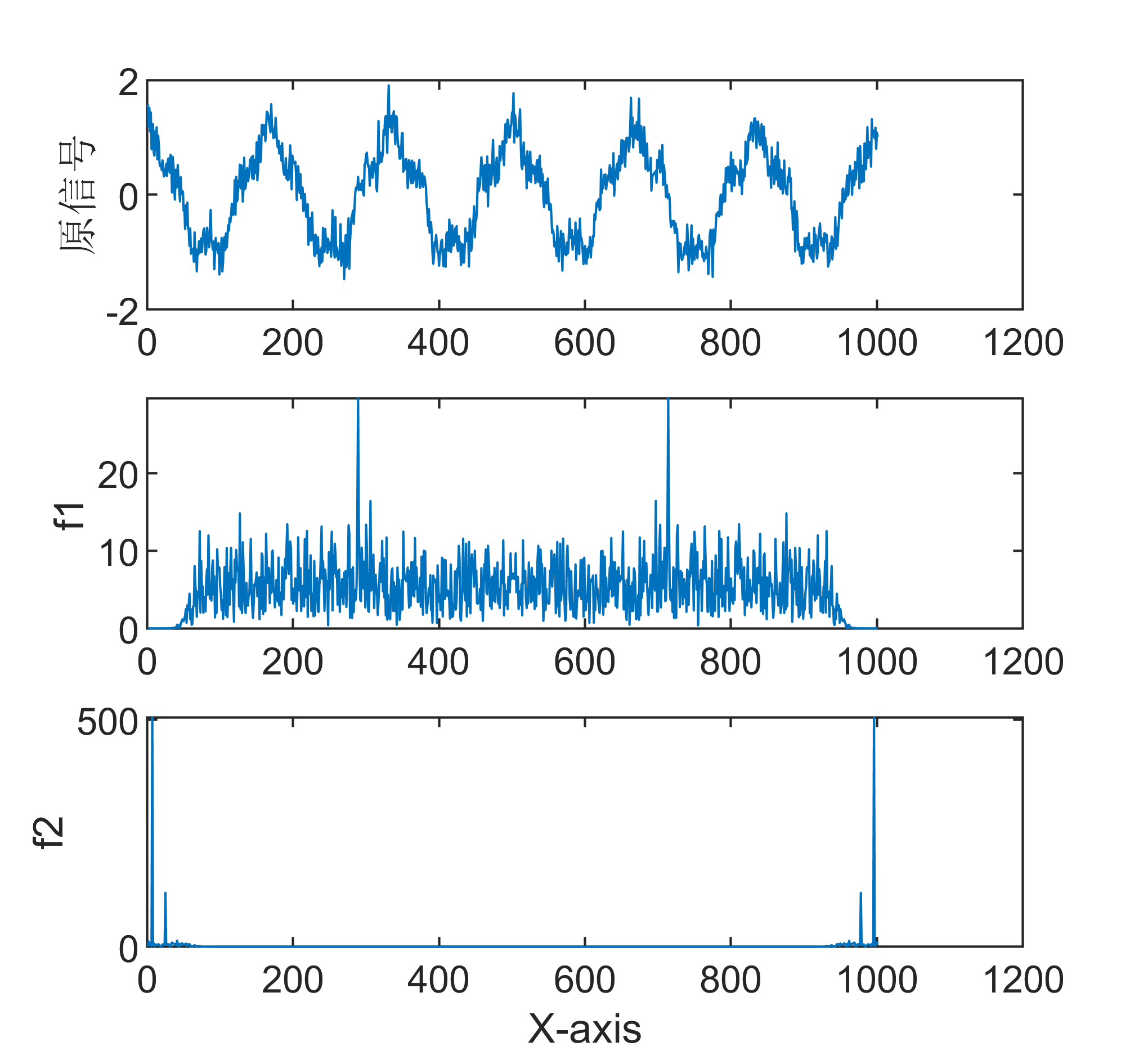
11【MATLAB】MLPTDenoise信号分解+FFT傅里叶频谱变换联合算法

MLPTDenoise（Multi-Level and Multi-Scale Principal Trend Denoising）是一种多级、多尺度主导趋势去噪方法。它是通过将信号分解为多个层次和尺度的主导趋势，进而去除噪声和冗余信息。MLPTDenoise的主要步骤如下：

1. 对原始信号进行小波变换，得到多个尺度的小波系数。

2. 对每个小波系数进行主导趋势分解，得到该尺度上的主导趋势和细节信号。

3. 将每个尺度的主导趋势相加，得到该层次的主导趋势。

4. 将该层次的主导趋势作为信号的一部分，将细节信号作为噪声，对噪声进行滤波去除。

5. 将去除噪声后的信号进行重构，得到该层次的去噪信号。

6. 重复步骤 2~5，直到所有层次的信号都被分解和去噪，得到原始信号的 MLPTDenoise 分解。 MLPTDenoise 分解具有对噪声和冗余信息的较好抑制效果，同时能够保留信号的主导趋势信息，避免了传统方法中的信号失真问题。因此，MLPTDenoise 在信号处理、图像处理和模式识别等领域也得到了广泛的应用。

原始数据分解各分量示意图

傅里叶变换是一种数学方法，用于将一个信号分解成一系列正弦和余弦函数的和，从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用，包括音频处理、图像处理等。 具体来说，傅里叶变换的步骤如下：

1. 给定一个连续时间域函数f(t)，其中t为时间。

2. 对f(t)进行傅里叶变换，得到它的频率域表示F(ω)，其中ω为角频率。

3. F(ω)表示了f(t)中所有频率分量的幅度和相位信息。

4. 将F(ω)分解成一系列正弦和余弦函数的和，即： F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中，k为频率分量的序号，a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号，从而更好地理解信号的频率分量和周期性特征，同时也方便进行一些信号处理任务，例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理，计算量较大，在实时处理等场景下可能会存在较大的延迟。

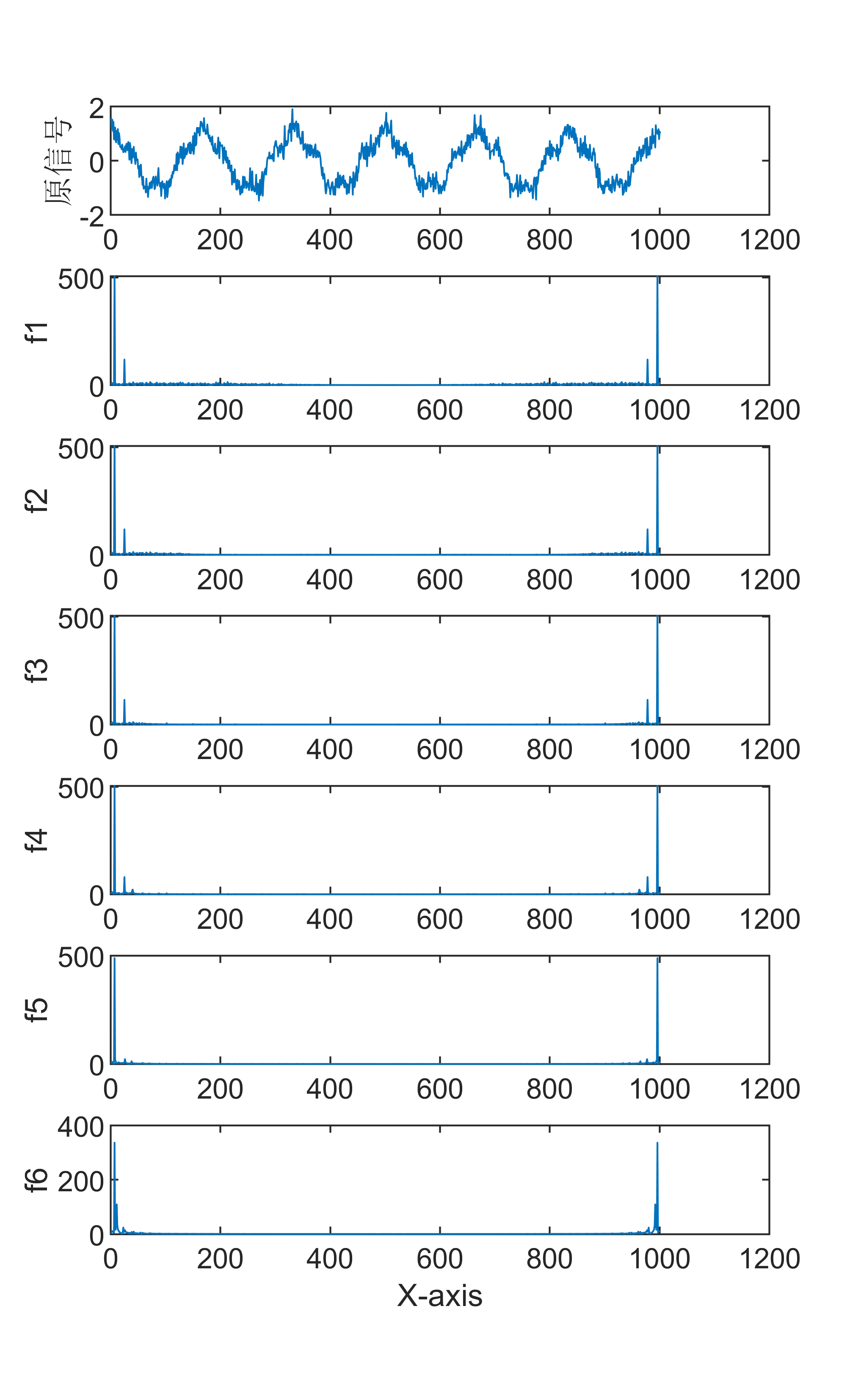
12【MATLAB】MODWT信号分解+FFT傅里叶频谱变换联合算法

MODWT（Maximal Overlap Discrete Wavelet Transform）是一种最大重叠离散小波变换方法，它是通过多级小波分解，将信号分解为不同尺度和频率的小波系数。MODWT的主要步骤如下：

1. 对原始信号进行多级小波分解，得到多个尺度和频率的小波系数。

2. 对每个尺度的小波系数进行重构，得到重构系数。

3. 对每个尺度的重构系数进行小波变换，得到该尺度的小波系数。

4. 将所有尺度的小波系数相加，得到原始信号的 MODWT 分解。 MODWT 分解具有对信号的多尺度分析能力，能够提供不同尺度和频率的信号信息。同时，MODWT 还能够避免传统小波变换中的信号失真问题，具有比较好的重构能力。因此，MODWT 在信号处理、图像处理和模式识别等领域也得到了广泛的应用。

原始数据分解各分量示意图

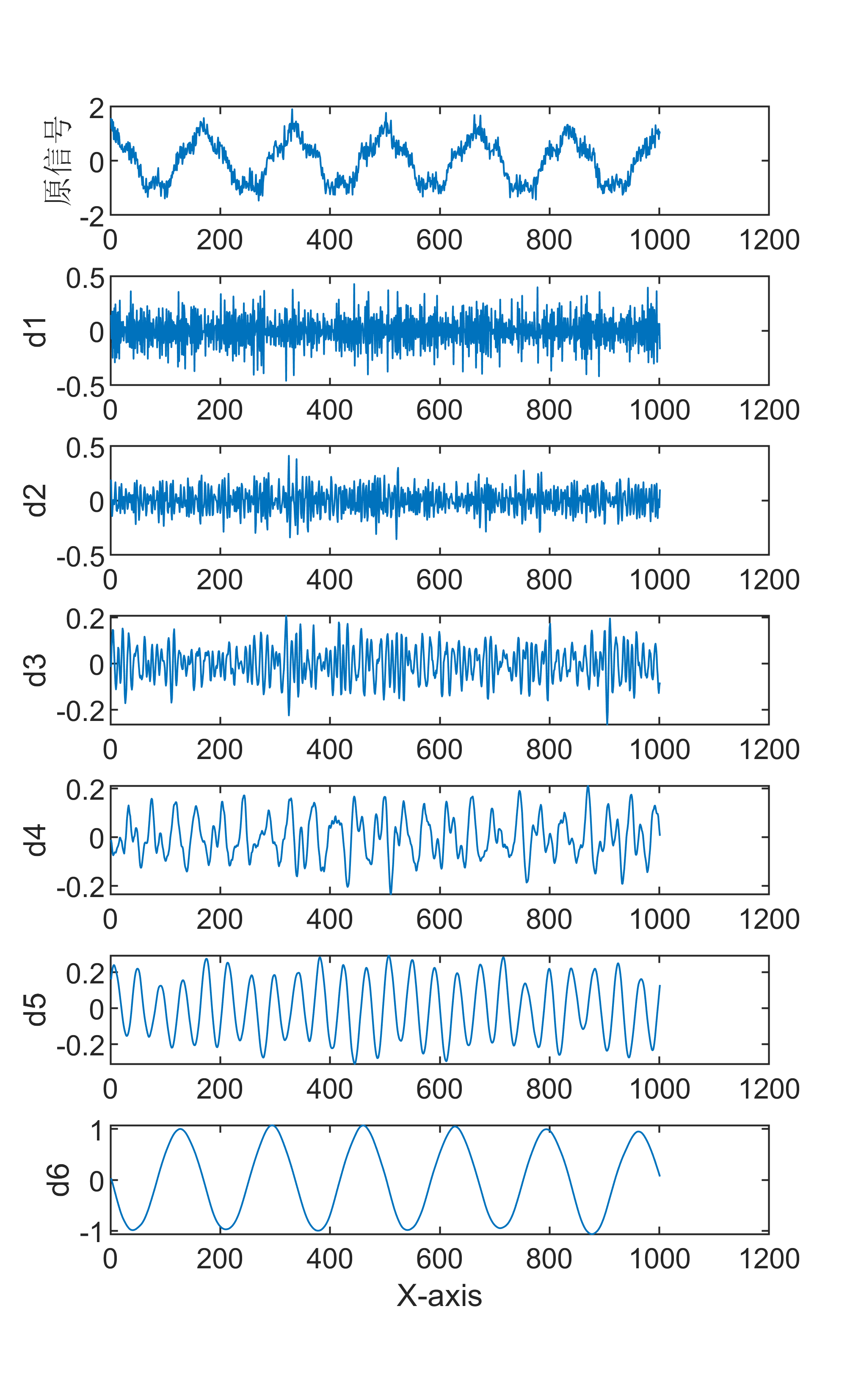
傅里叶变换是一种数学方法，用于将一个信号分解成一系列正弦和余弦函数的和，从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用，包括音频处理、图像处理等。 具体来说，傅里叶变换的步骤如下：

1. 给定一个连续时间域函数f(t)，其中t为时间。

2. 对f(t)进行傅里叶变换，得到它的频率域表示F(ω)，其中ω为角频率。

3. F(ω)表示了f(t)中所有频率分量的幅度和相位信息。

4. 将F(ω)分解成一系列正弦和余弦函数的和，即： F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中，k为频率分量的序号，a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号，从而更好地理解信号的频率分量和周期性特征，同时也方便进行一些信号处理任务，例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理，计算量较大，在实时处理等场景下可能会存在较大的延迟。

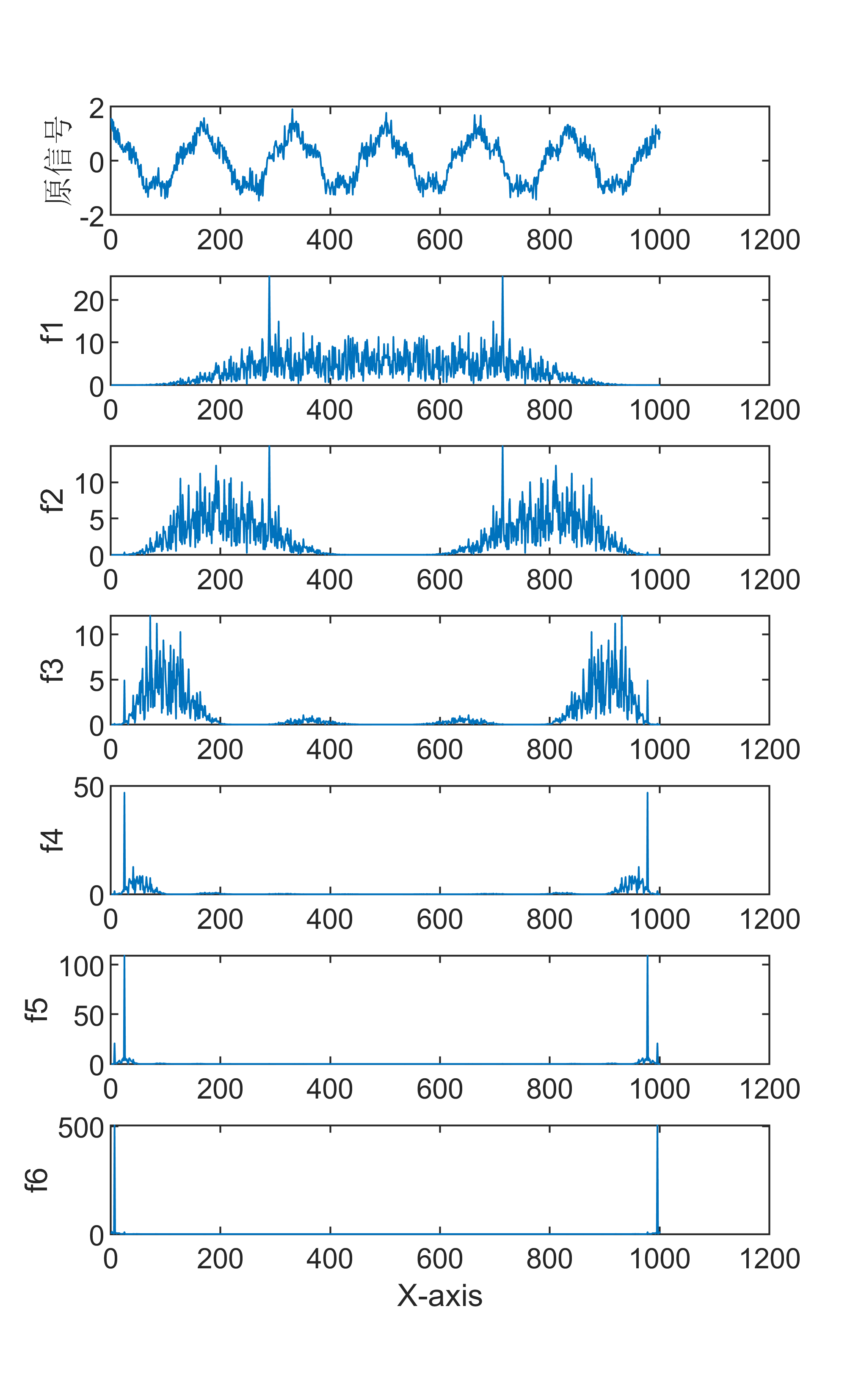
13【MATLAB】辛几何模态分解信号分解+FFT傅里叶频谱变换联合算法

辛几何模态分解（Symplectic Modal Analysis，SMA）是一种用于辛结构系统（如机械系统、光学系统等）振动分析的方法。它基于辛几何理论和模态分析方法，能够在保持系统辛结构的前提下，分解系统振动模态，并得到相应的振动频率和阻尼比。具体来说，辛几何模态分解首先将辛结构系统的运动方程转化为哈密尔顿形式，并通过辛几何积分方法求解系统的运动轨迹。然后，通过对系统轨迹进行奇异值分解（SVD），可以得到系统的振动模态及其阻尼比和振动频率。相比于传统的有限元方法，辛几何模态分解能够更准确地描述系统的振动行为，并且可以避免传统方法中出现的不物理的振动模态。辛几何模态分解在机械系统、光学系统、天体力学等领域有着广泛的应用，例如用于光学望远镜的振动分析、用于机械系统的结构优化等。

原始数据分解各分量示意图

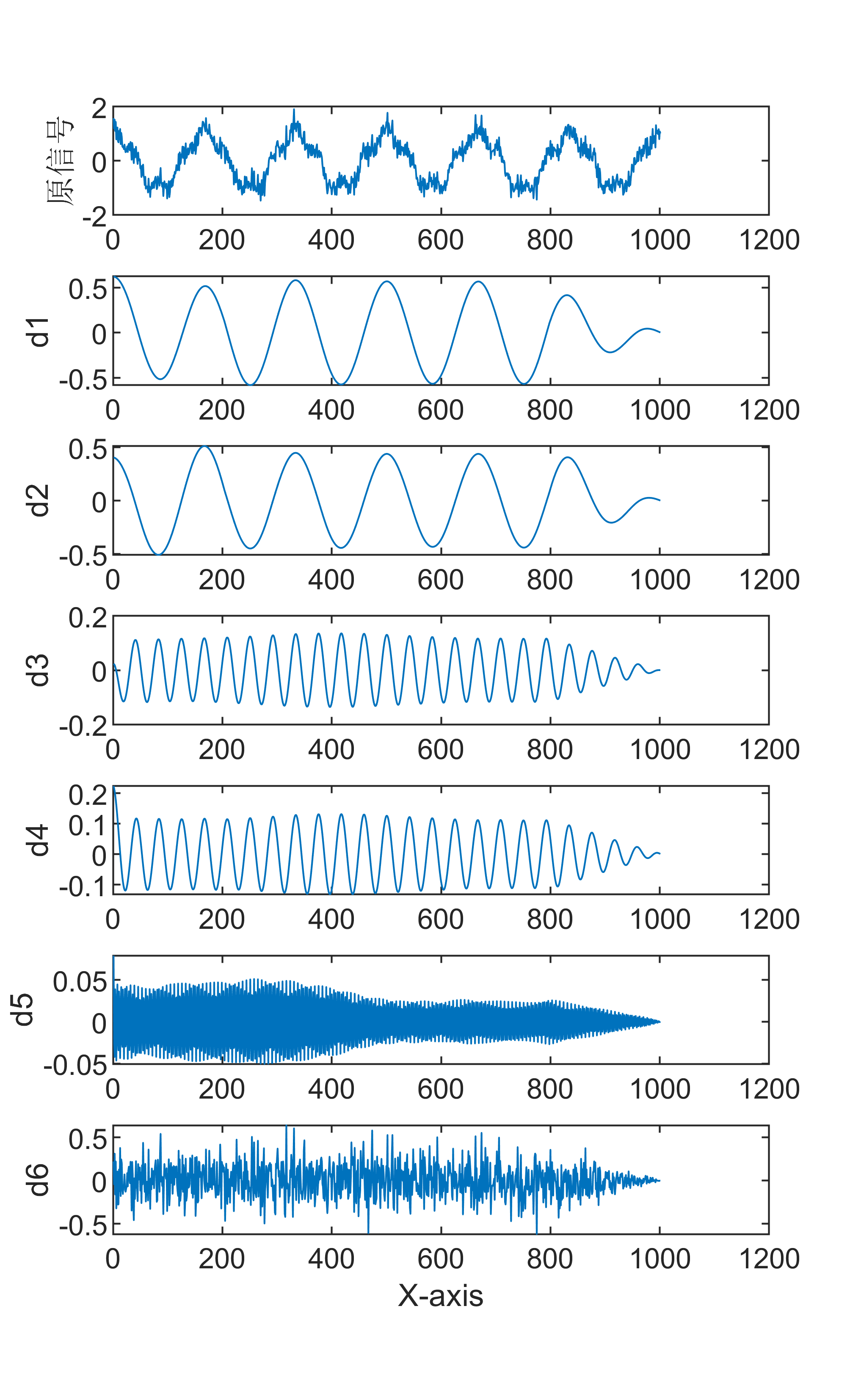
傅里叶变换是一种数学方法，用于将一个信号分解成一系列正弦和余弦函数的和，从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用，包括音频处理、图像处理等。 具体来说，傅里叶变换的步骤如下：

1. 给定一个连续时间域函数f(t)，其中t为时间。

2. 对f(t)进行傅里叶变换，得到它的频率域表示F(ω)，其中ω为角频率。

3. F(ω)表示了f(t)中所有频率分量的幅度和相位信息。

4. 将F(ω)分解成一系列正弦和余弦函数的和，即： F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中，k为频率分量的序号，a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号，从而更好地理解信号的频率分量和周期性特征，同时也方便进行一些信号处理任务，例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理，计算量较大，在实时处理等场景下可能会存在较大的延迟。

【MATLAB】全网唯一的13种信号分解+FFT傅里叶频谱变换联合算法全家桶

具体算法获取见文章顶部~