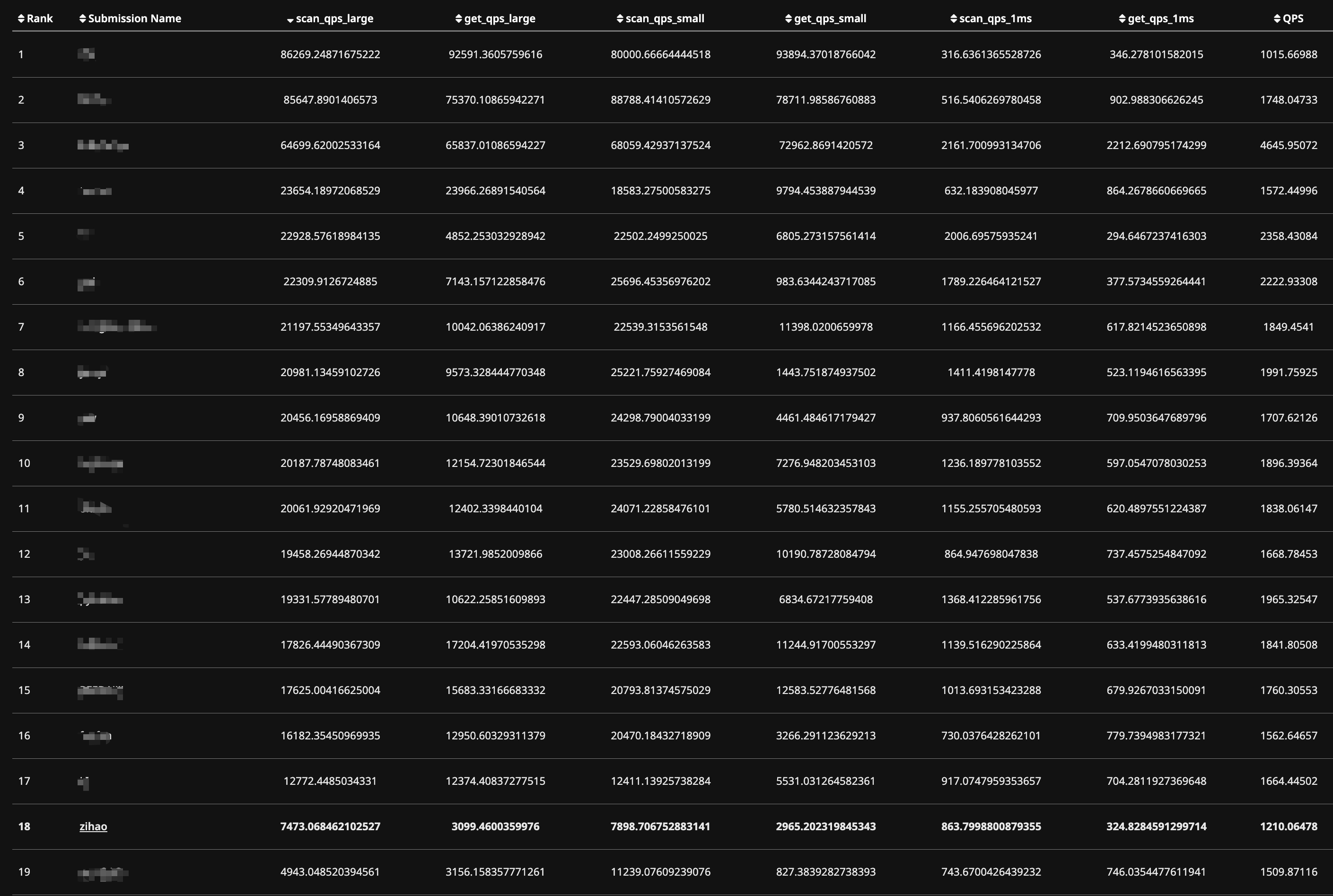
在这篇中，我们将关注如何将图表示为矩阵，并讨论我们可以探索的后续属性。我们定义了PageRank的概念，进一步探索随机游走，并引入矩阵分解作为生成节点嵌入的视角。在第一部分，我们将介绍PageRank作为在图中对节点重要性进行排序的方法。在这样做时，我们提出了PageRank的矩阵公式，并展示了与解决图上随机游走的平稳分布的联系。

在后续中，我们将图表示为矩阵：

• 这可以让我们通过随机游走去定节点的重要性。
• 可以通过矩阵分解方法获得节点embedding

1. 将网络视为图结构

将网页看作有向图，以链接指向作为边的方向（这个网页/节点能直接跳转到的网页就作为其下一个节点successor）将网页看作有向图，以链接指向作为边的方向（这个网页/节点能直接跳转到的网页就作为其下一个节点successor）：

其他可表现为有向图形式的信息网络示例：论文引用，百科全书中词条间的互相引用：

将Web网络看作有向图结构：

2. 给不同页面（节点）排序：

3. Link Analysis 算法

1. 在图中，我们想要定义节点的重要性，通过网络图链接结构来为网页按重要性分级rank。目前有3种常见用以计算图中节点重要性的方法：
2. PageRank
3. Personalized PageRank (PPR)
4. Random Walk with Restarts

衡量节点重要性：认为一个节点的链接越多，那么这个节点越重要。有向图有in-coming links和out-going links两种情况。可以想象，in-links比较不容易造假，比较靠谱，所以用in-links来衡量一个节点的重要性。可以认为一个网页链接到下一网页，相当于对该网页重要性投了票（vote）。所以我们认为一个节点的in-links越多，那么这个节点越重要。同时，我们认为来自更重要节点的in-links，在比较重要性时的权重更大。这就成了一个递归的问题。所以要计算一个节点的重要性就要先计算其前驱节点的重要性，计算这些前驱节点的重要性又要先计算它们前驱节点的重要性。

3.1 Links as votes思想

3.2 PageRank——流式模型

1. ageRank是谷歌搜索用的算法，用于对网页的重要性进行排序。在搜索引擎应用中，可以对网页重要性进行排序，从而辅助搜索引擎结果的网页排名。
2. 在现实世界中，将整个互联网视作图

主要思想：

矩阵形式：

举例：

3.3 与Random Walk联系

3.4 与特征向量联系

4. 总结