在我前面的一篇文章中讲解实现了基于改进的yolov5s-spd模型实现了五子棋目标对象检测模型系统的设计开发，这里紧接前文，突发奇想，是否可以借鉴同样的思路实现象棋的检测模型开发呢？理论上面肯定是可以的，但是实际效果如何就不知道了，五子棋数据相对而言比较简单只有黑子和白子两种对象性，象棋或者是军旗就不一样了，目标对象还是很多的，这里本来是想做中国象棋的目标检测的但是暂时还没有得到好用的数据集，所以这里就先做国际象棋的检测模型开发了，直接看下效果：

 针对五子棋目标检测的文章如下，感兴趣的话可以自行移步阅读。

《yolov5s融合SPD-Conv用于提升小目标和低分辨率图像检测性能实践五子棋检测识别》

今天主要是基于原生的yolov5s模型来开发模型，前文是针对小目标进行了相应的改进融合开发的模型。

这里的数据集本身质量不高，数据直接爬取的，有效数据不足100张，所以从推理识别检测的效果也能看出来，的确是效果还是比较一般的，后期有时间的话再构建一个高质量的大批次的数据集重新做一下吧，这里主要是实践一下整个流程。

yolov5官方项目在这里，截图如下所示：

 社区依旧是十分活动，截止目前已获得34k的star量了。

已经发布了10个版本了，如下：

 这里直接拉取官方项目即可，我是用的是yolov5s系列的模型，yaml文件如下；

# Parameters
nc: 12  # number of classes
depth_multiple: 0.33  # model depth multiple
width_multiple: 0.50  # layer channel multiple
anchors:
  - [10,13, 16,30, 33,23]  # P3/8
  - [30,61, 62,45, 59,119]  # P4/16
  - [116,90, 156,198, 373,326]  # P5/32


#Backbone
backbone:
  # [from, number, module, args]
  [[-1, 1, Conv, [64, 6, 2, 2]],  # 0-P1/2
   [-1, 1, Conv, [128, 3, 2]],  # 1-P2/4
   [-1, 3, C3, [128]],
   [-1, 1, Conv, [256, 3, 2]],  # 3-P3/8
   [-1, 6, C3, [256]],
   [-1, 1, Conv, [512, 3, 2]],  # 5-P4/16
   [-1, 9, C3, [512]],
   [-1, 1, Conv, [1024, 3, 2]],  # 7-P5/32
   [-1, 3, C3, [1024]],
   [-1, 1, SPPF, [1024, 5]],  # 9
  ]


# Head
head:
  [[-1, 1, Conv, [512, 1, 1]],
   [-1, 1, nn.Upsample, [None, 2, 'nearest']],
   [[-1, 6], 1, Concat, [1]],  # cat backbone P4
   [-1, 3, C3, [512, False]],  # 13

   [-1, 1, Conv, [256, 1, 1]],
   [-1, 1, nn.Upsample, [None, 2, 'nearest']],
   [[-1, 4], 1, Concat, [1]],  # cat backbone P3
   [-1, 3, C3, [256, False]],  # 17 (P3/8-small)

   [-1, 1, Conv, [256, 3, 2]],
   [[-1, 14], 1, Concat, [1]],  # cat head P4
   [-1, 3, C3, [512, False]],  # 20 (P4/16-medium)

   [-1, 1, Conv, [512, 3, 2]],
   [[-1, 10], 1, Concat, [1]],  # cat head P5
   [-1, 3, C3, [1024, False]],  # 23 (P5/32-large)

   [[17, 20, 23], 1, Detect, [nc, anchors]],  # Detect(P3, P4, P5)
  ]

这里一共有12种目标对象需要检测识别，直接修改原始yaml中nc=12即可。

数据样例如下：

 单样本标注实例如下所示：

11 0.32125 0.851111 0.0525 0.075556
8 0.375 0.857778 0.045 0.08
6 0.43625 0.848889 0.0425 0.071111
10 0.48625 0.866667 0.0475 0.088889
7 0.55125 0.853333 0.0475 0.088889
6 0.6175 0.84 0.04 0.071111
8 0.67375 0.851111 0.0475 0.084444
11 0.74625 0.851111 0.0525 0.075556
9 0.74 0.744444 0.04 0.066667
9 0.6675 0.737778 0.035 0.062222
9 0.6125 0.733333 0.035 0.062222
9 0.55375 0.731111 0.0325 0.057778
9 0.49375 0.737778 0.0325 0.062222
9 0.43625 0.735556 0.0325 0.057778
9 0.37875 0.746667 0.0375 0.062222
9 0.32125 0.742222 0.0375 0.062222
3 0.32875 0.26 0.0375 0.066667
3 0.38375 0.257778 0.0325 0.071111
3 0.44375 0.244444 0.0325 0.071111
3 0.4925 0.257778 0.035 0.071111
3 0.54875 0.255556 0.0325 0.066667
3 0.60625 0.248889 0.0325 0.071111
3 0.66375 0.235556 0.0325 0.071111
3 0.7175 0.248889 0.035 0.071111
5 0.72 0.128889 0.045 0.097778
5 0.3275 0.162222 0.045 0.093333
2 0.38625 0.157778 0.0425 0.102222
2 0.6625 0.142222 0.045 0.097778
0 0.59875 0.14 0.0375 0.093333
0 0.44 0.133333 0.04 0.097778
4 0.49875 0.131111 0.0425 0.12
1 0.55125 0.131111 0.0425 0.128889

完成数据集构建之后就可以开启模型训练了，训练日志输出如下所示：

 前文也说到了数据集存在的问题，这里训练结束可以看到：实际的评估效果并不十分理想。

简单看下对应的结果输出：

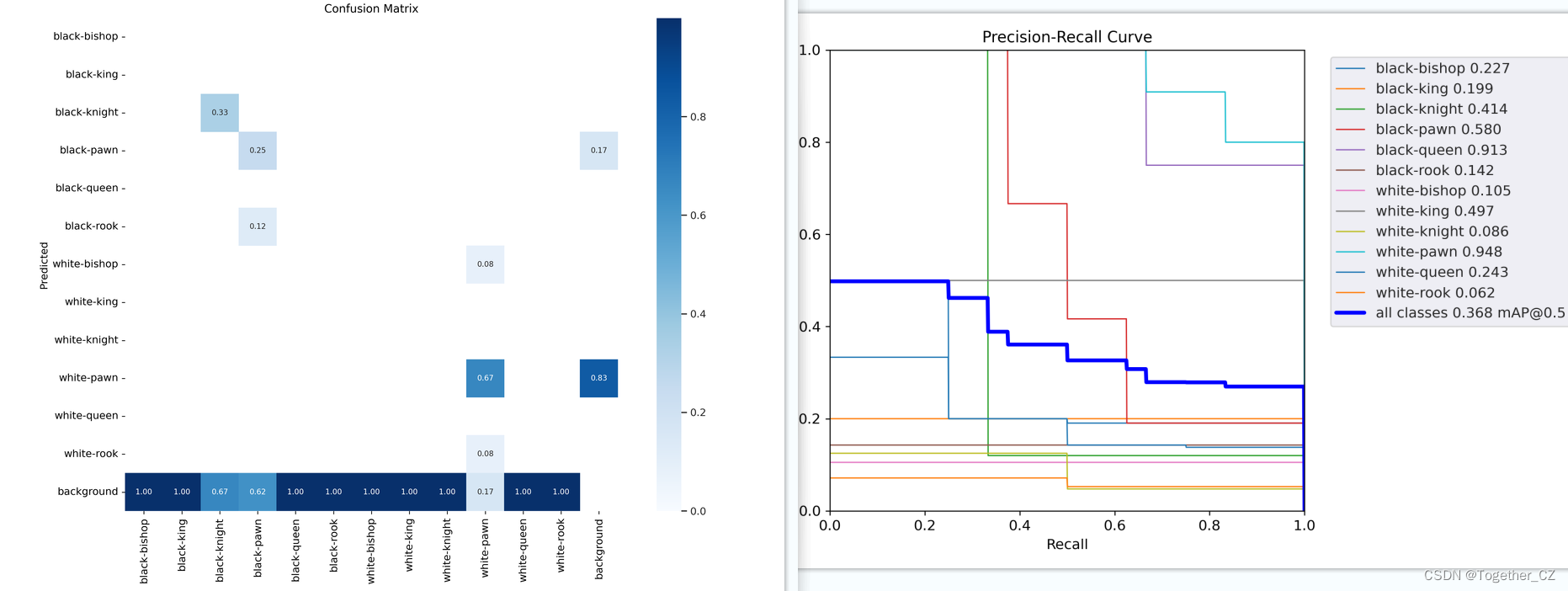
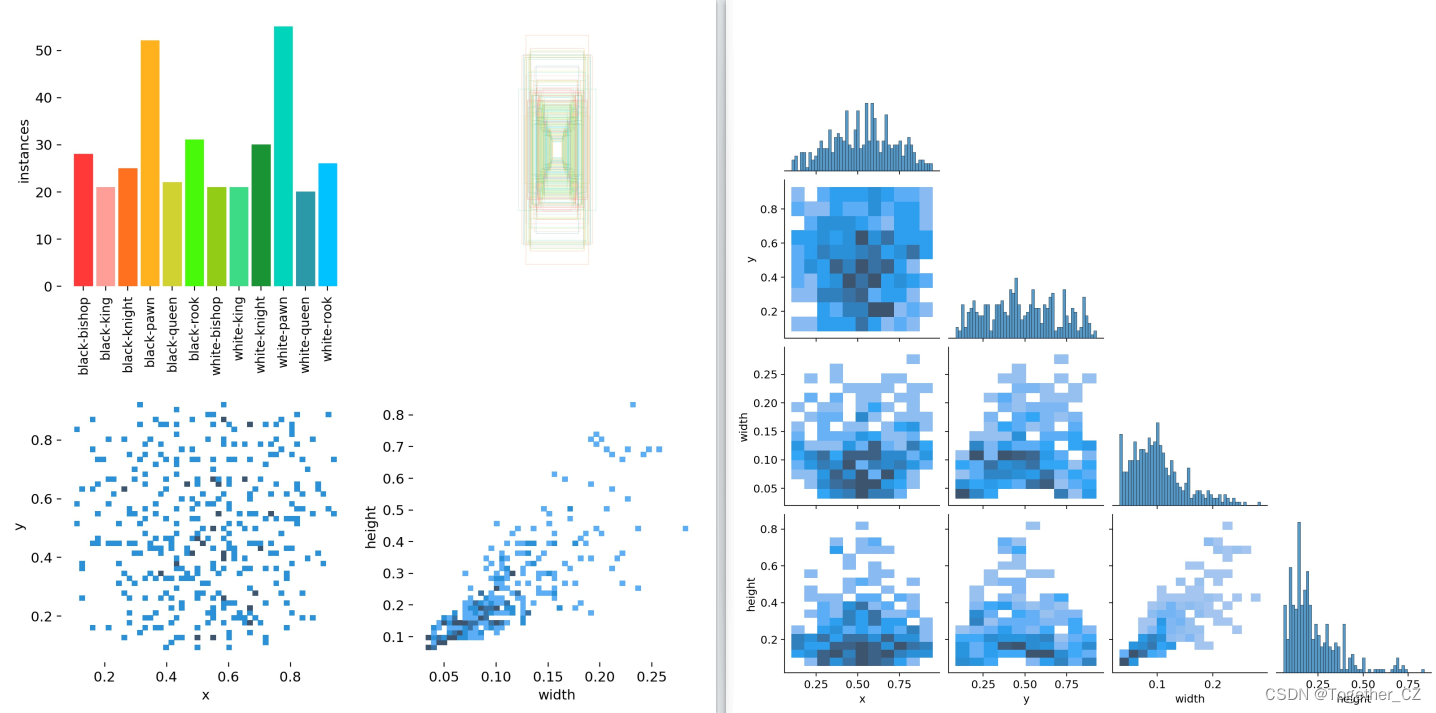
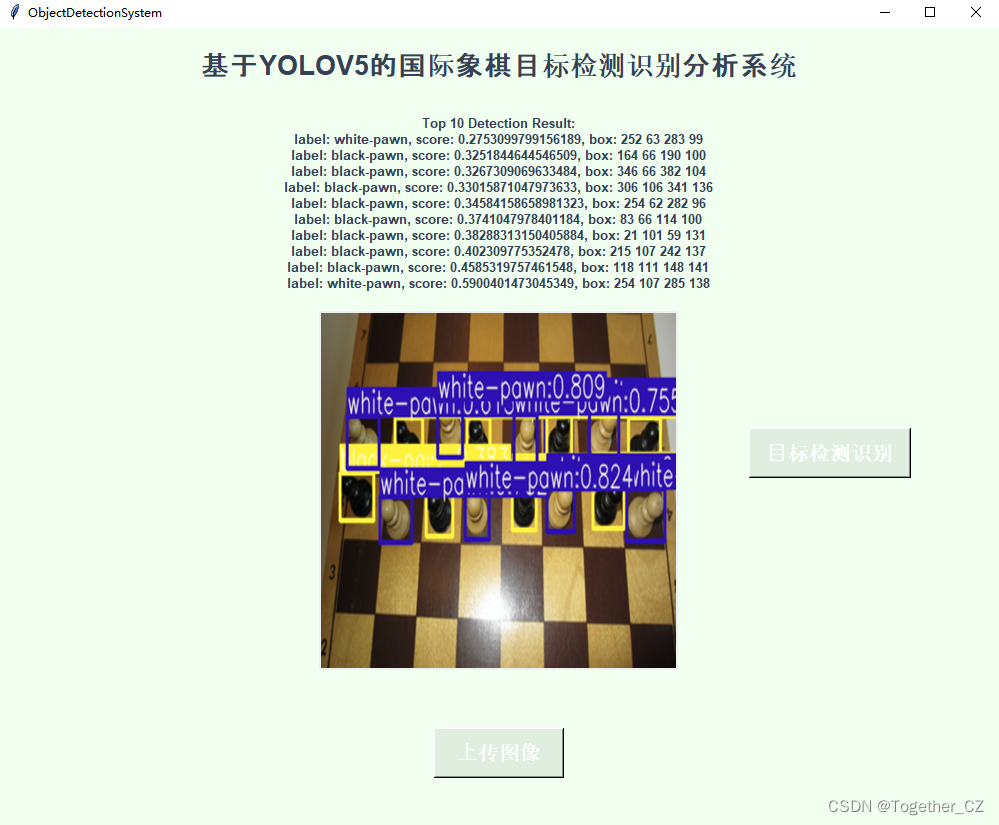
 这里同样是为了更加简洁直观地使用模型，编写了对应的界面来使得推理可视化，如下：

 上传单张图像：

 启动推理检测：