从今天起,我们将要开始数论的学习,是不是感觉很难?难的话就听我讲吧,讲了后就不难了(bushi)
数论函数定义 (数论函数)
数论函数的定义:在全体正整数（或者整数）上定义的函数称作数论函数。
积性的定义：若 gcd(a,b)=1,
则f(ab)
=f(a)f(b)
。
举个栗子:
欧拉函数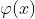
:
![1(x)=1,Id(x)=x,I(x)=[x=1]](https://latex.codecogs.com/gif.latex?1%28x%29%3D1%2CId%28x%29%3Dx%2CI%28x%29%3D%5Bx%3D1%5D)
。
接下来,我们再举一个函数,狄利克雷卷积:
数论函数f(n)
和g(n)
的狄利克雷卷积h(n)
定义为：
记作h=f*g;
定理:两个积性函数的狄利克雷卷积也是积性函数。
那我们是如何证明的呢,那可就说来话长了:
看到这么长一串的函数,我的心就发抖………
定理:两个积性函数的对应位置相乘也是积性函数。
这个就很显然了,证明我就不给出来了,你们自己想着吧。
所以我们可以定义更多的数论函数，以及用卷积描述它们之间的关系：
例如:
1,即
,即
接下来,我们来研究一下,卷积的性质:
定理(卷积运算律):
交换律：设有两个积性函数f,g
则
结合律：设有两个积性函数f,g,h
则
这不就是乘法结合律吗?小学生都会好不好……
交换律的证明很显然。
结合律的证明可以把式子改写成矩阵形式，然后用矩阵的结合律
来证明。应该大力推式子也可以。
单位元的定理:
I是单位元:对任意的数论函数
;
证明过程如下:
接下来又来到了下一个函数,狄利克雷逆:
若
,则数论函数f,g互为彼此的狄利克雷逆。
整数分块
接下来,我们进入下一个章节的学习:整数分块
定理:对于任意的,
只有
种取值
证明过程如下:
当时,
只有
种取值
当时,
,也只有
种取值
综上,只有种取值
下面举个栗子:
计算下取整分式的和式,计算
由于只有
种取值 ,并且,使得
取相同的取值的
也是一段一段的，所以我们只需要一段一段地计算即可。
res=0;
for(int l=1,r;l<=n;l=r+1){
r=n/(n/l);
res+=(r-l+1)*(n/l);
}哎哟,终于讲完了,累死我了,咱么今天就讲到这里,下篇博文我们会讲莫比乌斯反演,记得来收看哦!!
