题目如下：

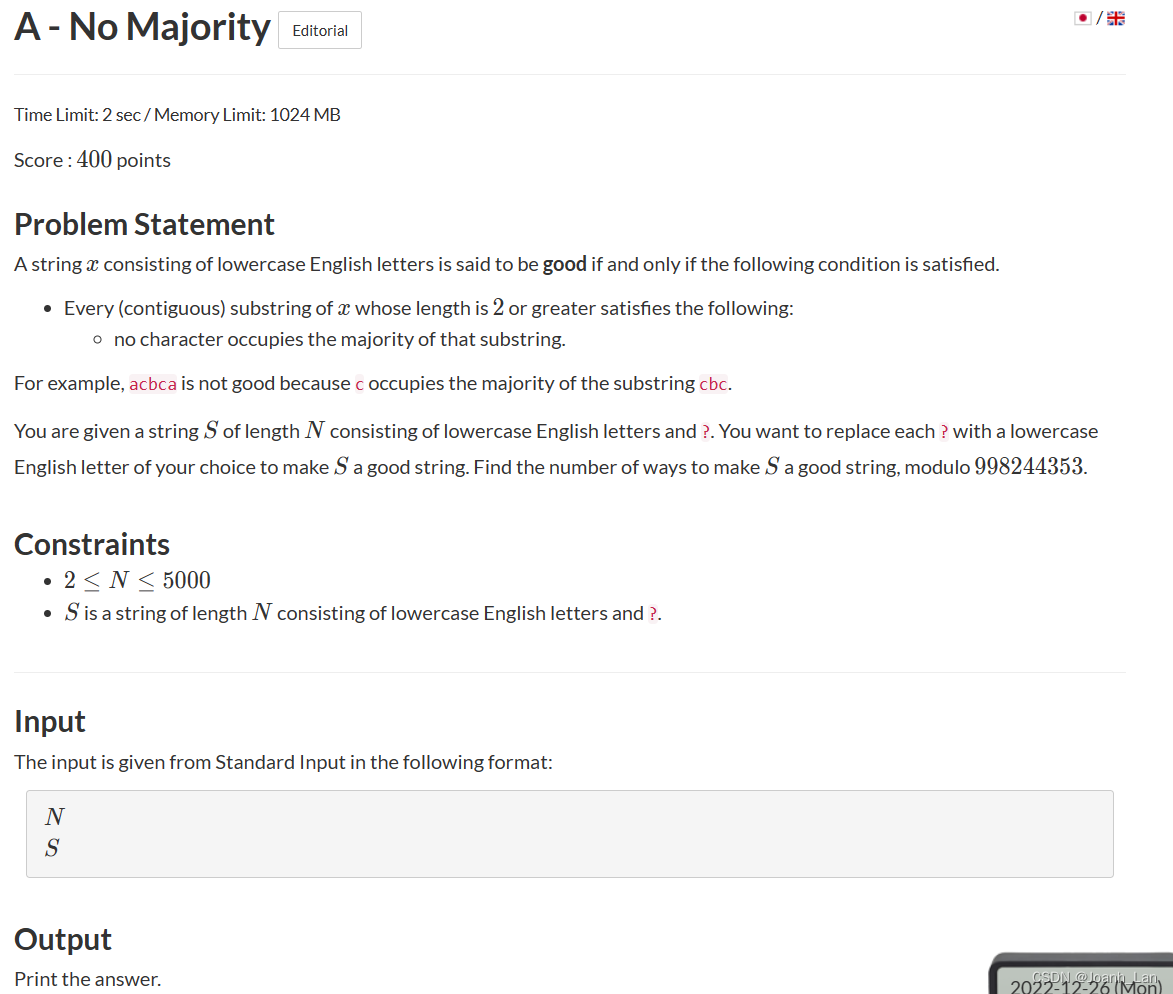
思路 or 题解：

对于一个子串， 如果长度为 $len$, 如果该子串中任意一个字符的出现个数 大于 $\frac{len}{2}$ 那该字符串为 $Ungood$ 串
反之，如果任意子串， 长度设为 $len$, 如果该子串中任意一个字符的出现个数 小于等于 $\frac{len}{2}$， 那该字符串为 $Good$ 串

核心：
如果一个子串有字符超过一半，那肯定可以找到一个长度 $\le 3$ 的子串满足字符超过一半。

我们可以用 DP(动态规划) 的思想去写
$dp[i][j][k]$, $i$位置, $i$位置字符为$j$， $i-1$位置字符为 $k$ 的合法方案数。

转移：
判断合法，如果合法：
$dp[i][j][k]=(dp[i][j][k]+dp[i-1][k][z])$

时间复杂度: $O(n\times 26^3)$

AC 代码如下：

const int mod = 998244353;
const int inf = 2147483647;
const int N = 5009;
int n;
char s[N];
int dp[N][27][27];
bool check(int a, char aa, int b, char bb)
{
    if ((aa != '?' && aa - 'a' != a) || (bb != '?' && bb - 'a' != b))
        return false;
    return true;
}
bool check2(int a, int b, int c)
{
    if (a == b || a == c || b == c)
        return false;
    return true;
}
void solve()
{
    cin >> n;
    cin >> s + 1;
    for (int i = 0; i < 26; i++)
        for (int j = 0; j < 26; j++)
            if (i != j && check(i, s[2], j, s[1]))
                dp[2][i][j] = 1;
        
    for (int i = 3; i <= n; i++)
        for (int j = 0; j < 26; j++)
            for (int k = 0; k < 26; k++)
                for (int z = 0; z < 26; z++)
                {
                    if (!check(j, s[i], k, s[i - 1]) || !check2(j, k, z))
                        continue;
                    dp[i][j][k] = (dp[i][j][k] + dp[i - 1][k][z]) % mod;
                }

    int ans = 0;
    for (int i = 0; i < 26; i++)
        for (int j = 0; j < 26; j++)
            ans = (ans + dp[n][i][j]) % mod;
    cout << ans << '\n';
}
int main()
{
    buff;
    solve();
}