ps：在教材上直接打开colab，运行原来的代码!pip install git+https://github.com/d2l-ai/d2l-zh@release # installing d2l是会报错的，改成这句代码，可以正确运行：!pip install d2l==0.14.，直接制定了d2l的版本

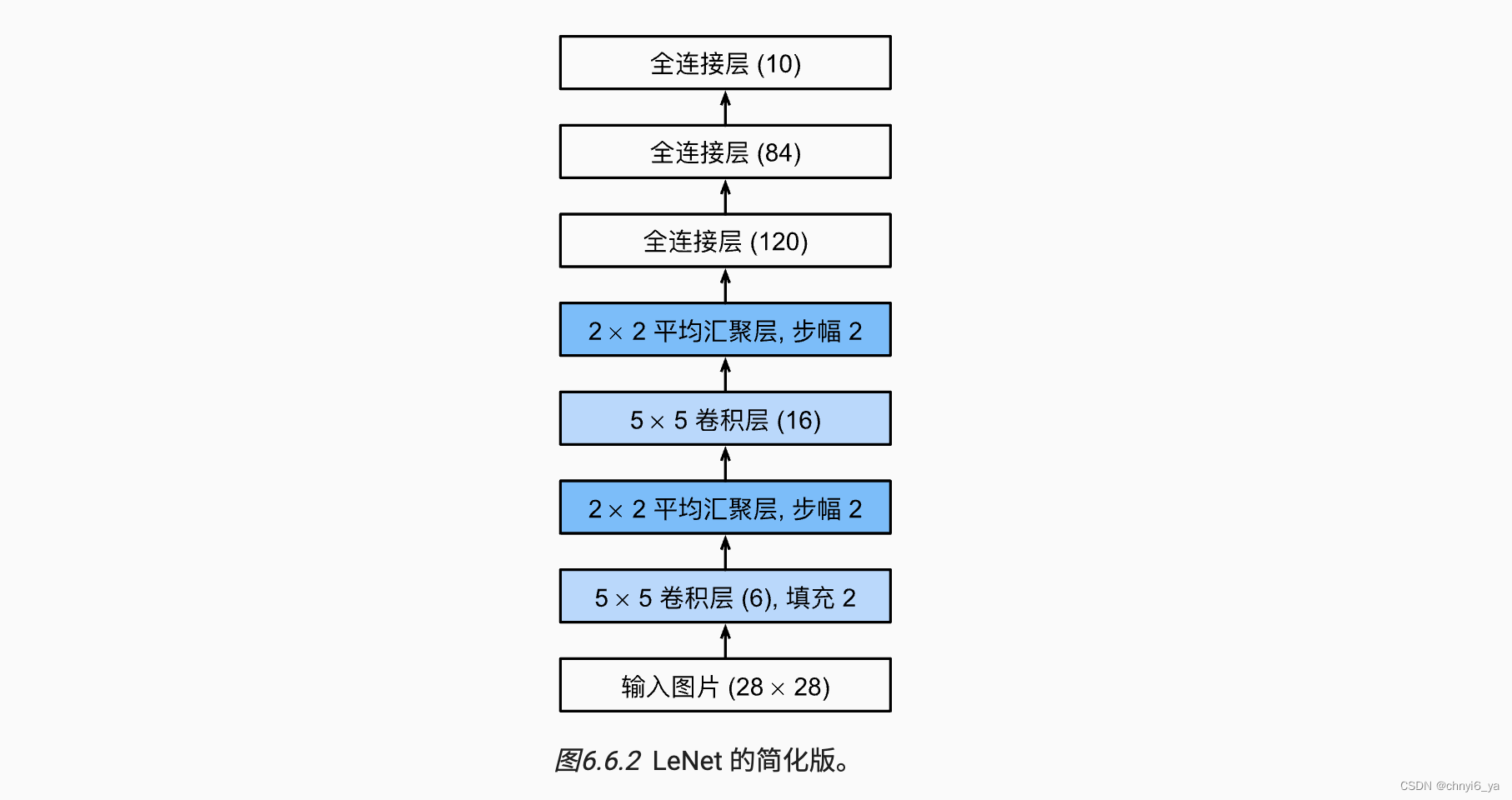
1. LeNet

总体来看，LeNet（LeNet-5）由两个部分组成：

• 卷积编码器：由两个卷积层组成;

• 全连接层密集块：由三个全连接层组成。

实例化一个Sequential块并将需要的层连接在一起。

import torch
from torch import nn
from d2l import torch as d2l

class Reshape(torch.nn.Module): # 这个函数是给输入用的
    def forward(self,x):
        # view函数是为了改变tensor形状为(batchsize，channels，x，y)
        return x.view(-1,1,28,28) # 28*28是输入图片大小
    
net = torch.nn.Sequential(
    # torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
    Reshape(),nn.Conv2d(1,6,kernel_size=5,padding=2),nn.Sigmoid(), # 为了得到非线性，要在卷积后面加上sigmoid激活函数
    nn.AvgPool2d(kernel_size=2,stride=2), # 也可以写成nn.AvgPool2d(2,stride=2)，第一个参数不用写参数名
    nn.Conv2d(6,16,kernel_size=5),nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2,stride=2),nn.Flatten(),# Flatten()将第一维（批量）保持住，其他展平为一个维度，输入到多层感知机
    nn.Linear(16 * 5 * 5 , 120),nn.Sigmoid(), # 线性层，输入时400，输出是120，用sigmoid激活一下
    nn.Linear(120, 84),nn.Sigmoid(), # 再把120 降到 84
    nn.Linear(84,10)) # 输入为 84， 输出为10

可以看到，最后是一个3层的，有两个隐藏层的多层感知机，前面是两个卷积层，每个卷积层后面有一个激活层和一个池化层。

2. 检查模型

检查模型，以确保其操作与我们期望的 图一致。

X = torch.rand(size=(1,1,28,28), dtype = torch.float32)
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape:\t' , X.shape)

运行结果如下：

在这里，卷积的作用就是把每一层输出变小，通道变多。每一个通道信息可以认为是一个空间的pattern（模式），不断地把空间信息压缩变小，通道数变多，可以把抽出来的压缩的信息放在不同的通道里面，最后MLP就把所有的模式拿出来然后训练到最后的输出。

3. 模型训练

现在我们已经实现了LeNet，让我们看看LeNet在Fashion-MNIST数据集上的表现。

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)

虽然卷积神经网络的参数较少，但与深度的多层感知机相比，它们的计算成本仍然很高，因为每个参数都参与更多的乘法。 通过使用GPU，可以用它加快训练。

# 如果模型已经在gpu上了，计算精度会在gpu上做
def evaluate_accuracy_gpu(net, data_iter, device=None): 
    """使用GPU计算模型在数据集上的精度"""
    # isinstance(object, classinfo)：object – 实例对象，classinfo – 可以是直接或间接类名、基本类型或者由它们组成的元组
    # 返回值：如果对象的类型与参数二的类型（classinfo）相同则返回 True，否则返回 False。
    if isinstance(net, nn.Module):
      # 如果net是 troch.nn实现的版本，与之相对的是手写的版本
        net.eval()  # 设置为评估模式，不用计算和更新梯度，eval（）模式与之相对的是train（）
        if not device: # 如果没有设备
            device = next(iter(net.parameters())).device # 设置为网络层所在的设备
    # 正确预测的数量，总预测的数量
    metric = d2l.Accumulator(2)
    with torch.no_grad():
        for X, y in data_iter:
            if isinstance(X, list): # 如果X是一个list
                # BERT微调所需的（之后将介绍）
                X = [x.to(device) for x in X] # 把每一个x都挪到device中
            else:
                X = X.to(device) # 如果不是list，挪一次就够了
            y = y.to(device) # 把y也挪到device上
            metric.add(d2l.accuracy(net(X), y), y.numel())
    return metric[0] / metric[1] # 分类正确的个数/总个数

为了使用GPU，我们还需要一点小改动，在进行正向和反向传播之前，我们需要将每一小批量数据移动到我们指定的设备（例如GPU）上。

如下所示，训练函数train_ch6也类似于之前定义的train_ch3。 由于我们将实现多层神经网络，因此我们将主要使用高级API。 以下训练函数假定从高级API创建的模型作为输入，并进行相应的优化。 我们使用Xavier随机初始化模型参数。 与全连接层一样，我们使用交叉熵损失函数和小批量随机梯度下降。

def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):
    """用GPU训练模型(在第六章定义)"""
    def init_weights(m): # 初始化权重
        if type(m) == nn.Linear or type(m) == nn.Conv2d: # 如果是全连接层或者卷积层
            nn.init.xavier_uniform_(m.weight) # 使用Xavier初始化：nn.init.xavier_uniform_
    net.apply(init_weights) # 使net的每一层都应用一下初始化权重函数
    print('training on', device) # 打印一下在哪个device上训练
    net.to(device) # 把net挪到device上
    optimizer = torch.optim.SGD(net.parameters(), lr=lr) # 使用了 SGD优化器
    loss = nn.CrossEntropyLoss() # 使用交叉熵损失函数
    animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
                            legend=['train loss', 'train acc', 'test acc'])# animator动画效果
    timer, num_batches = d2l.Timer(), len(train_iter) # d2l.Timer()是一个计时器
    for epoch in range(num_epochs): # 对每一次数据做迭代
        # 训练损失之和，训练准确率之和，样本数
        metric = d2l.Accumulator(3)
        net.train() # 训练模式
        # enumerate函数用来遍历一个集合对象，它在遍历的同时还可以得到当前元素的索引位置
        for i, (X, y) in enumerate(train_iter): # 每一次迭代都拿到索引i，以及 一个batch的X和y
            timer.start() # 开始训练
            optimizer.zero_grad() # 优化器梯度清零
            X, y = X.to(device), y.to(device) #把输入X和输出y挪到gpu上
            y_hat = net(X) # 得到X的预测值y_hat
            l = loss(y_hat, y) # 计算损失：预测值和真实值之间的差距
            l.backward() # 反向传播计算得到每个参数的梯度值
            optimizer.step() # 通过梯度下降执行一步参数更新
            with torch.no_grad(): # l * X.shape[0] 样本数乘以平均损失=总的样本损失
                metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
            timer.stop() # 一个批量的训练结束
            train_l = metric[0] / metric[2] # 训练的损失
            train_acc = metric[1] / metric[2] # 训练的精度
            if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
                animator.add(epoch + (i + 1) / num_batches,
                             (train_l, train_acc, None)) # 绘制每5次迭代的训练损失和训练精度
        test_acc = evaluate_accuracy_gpu(net, test_iter) # 测试精度
        animator.add(epoch + 1, (None, None, test_acc)) # 绘制每一次迭代的测试精度
    print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
          f'test acc {test_acc:.3f}')
    print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec ' 
          f'on {str(device)}') # metric[2] * num_epochs：样本数，timer.sum()：训练完成需要的时间

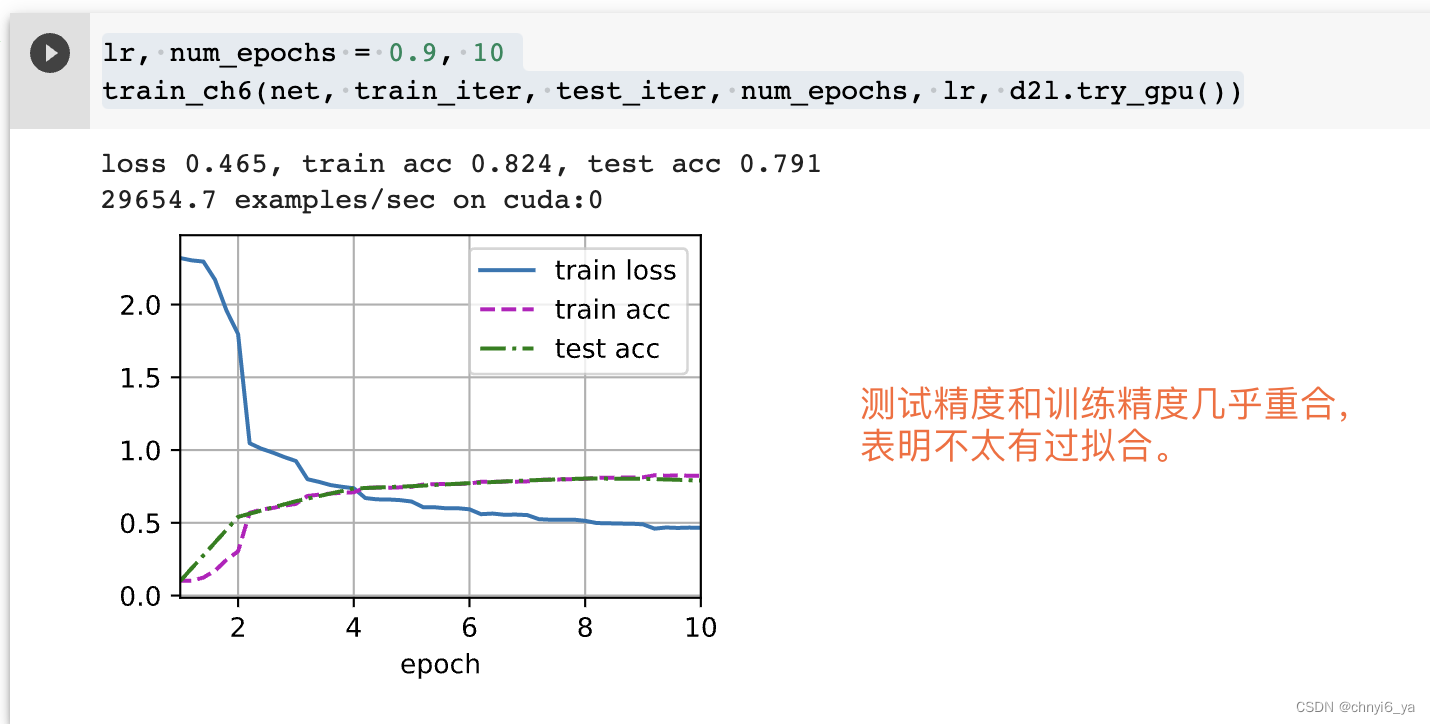
现在，我们[训练和评估LeNet-5模型]

lr, num_epochs = 0.9, 10
train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

4. 小结

• 卷积神经网络（CNN）是一类使用卷积层的网络。
• 在卷积神经网络中，我们组合使用卷积层、非线性激活函数和汇聚层。
• 为了构造高性能的卷积神经网络，我们通常对卷积层进行排列，逐渐降低其表示的空间分辨率，同时增加通道数。
• 在传统的卷积神经网络中，卷积块编码得到的表征在输出之前需由一个或多个全连接层进行处理。
• LeNet是最早发布的卷积神经网络之一。