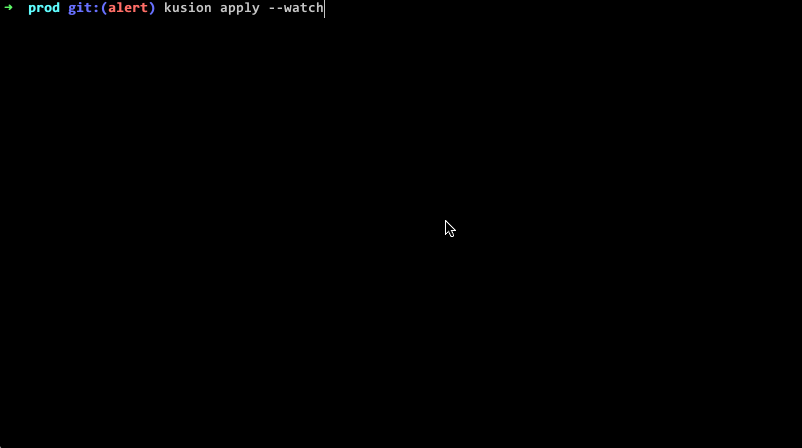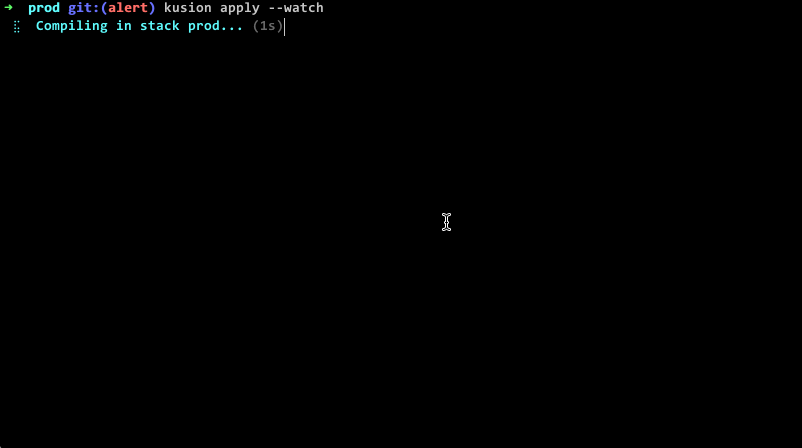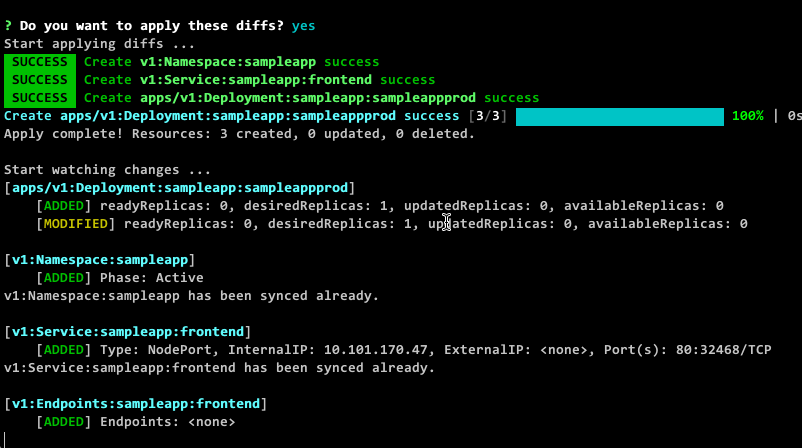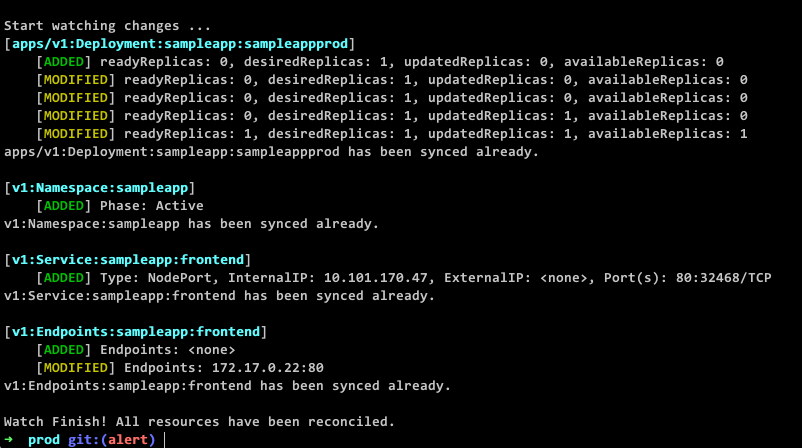
AC自动机

AC自动机是干嘛的？

我有一个敏感词数组，里面装的是所有的敏感词，还有一篇大文章，我要求出大文章里面所有的敏感词。

敏感词数组本身的组织是一颗前缀树。

AC自动机就是在前缀树的基础上做升级。

流程

我们在前缀树的基础上给每一个节点加上fail指针并且做出规定：头节点的fail指针一定指向null
头节点的下级直接节点的fail指针一律指向头部
在整颗前缀树全部建立完毕之后，再去建立fail指针
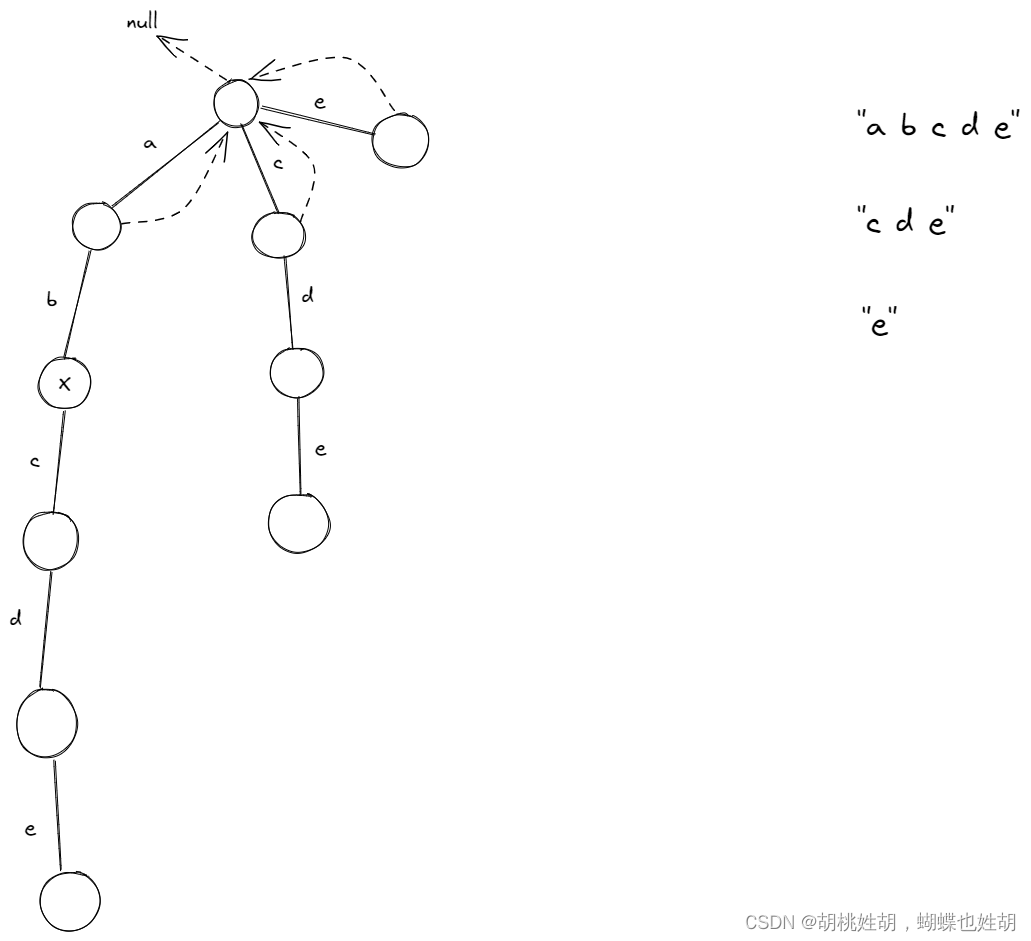
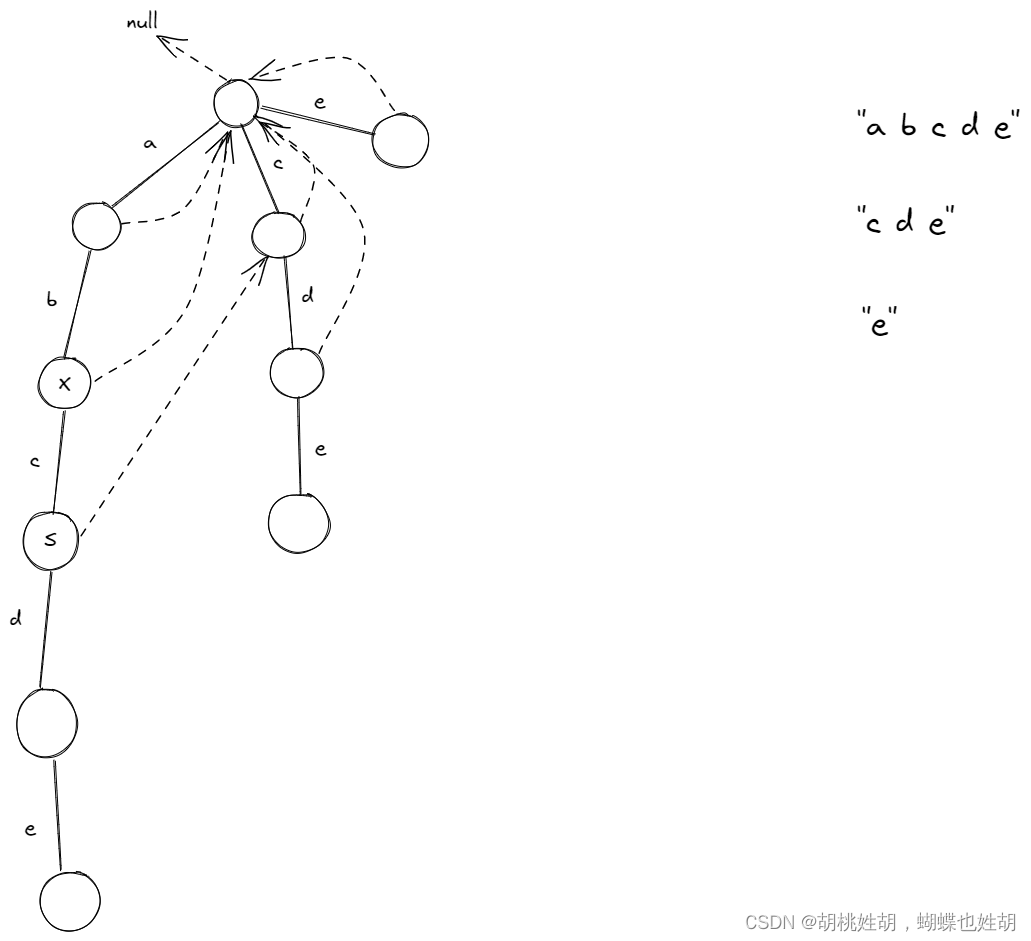
以下是其他节点的定义规则，看图说话。

请添加图片描述

假设有一个节点X，X的父亲节点P，P的fail指针指的是谁，看图可以知道指向的是头节点。
X的父亲节点到X的路径存放的是b，因此我询问X的父亲节点的fail指针指向的节点，也就是图中的头节点，你的路径中有没有b，可以看到头节点有的路径是a, c, e，没有b。
于是继续往跳，头部节点的fail指针指向的节点是null,null当然不会有b路径，因此X的fail指针直接指向头部
再看S节点。

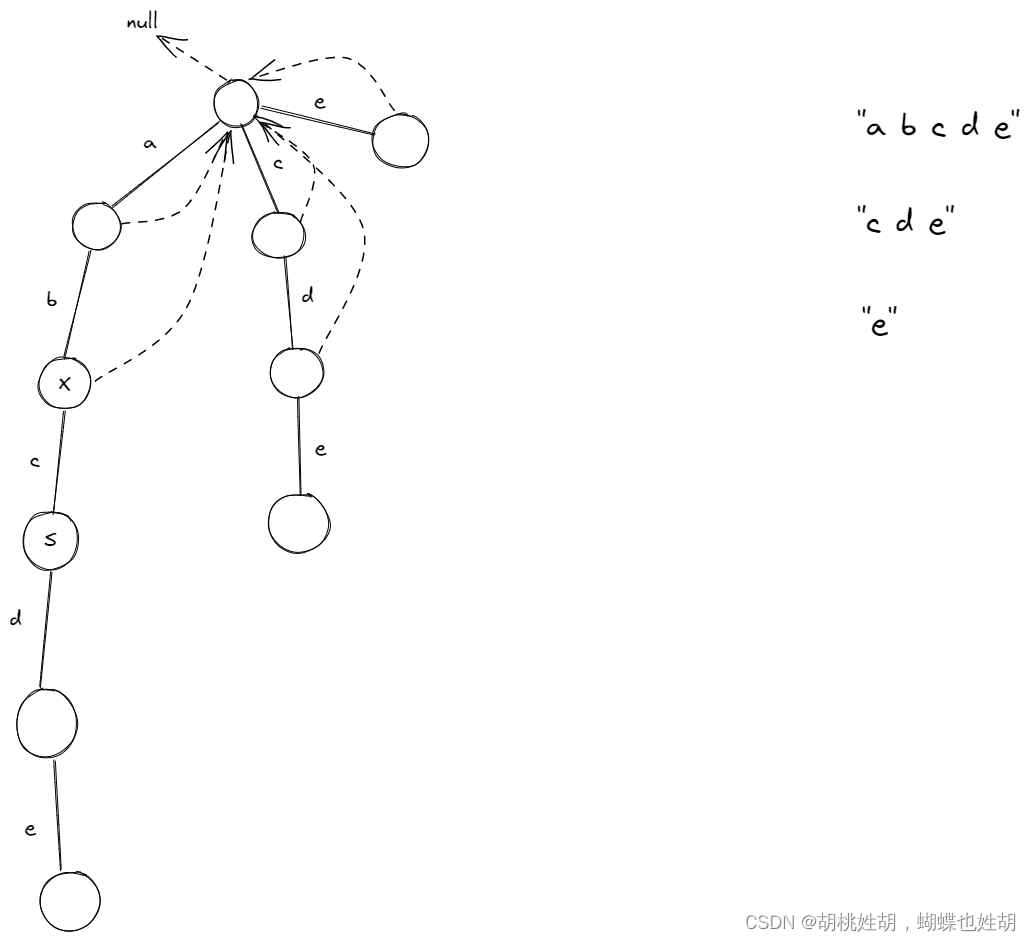
请添加图片描述

S的父亲节点X的fail指针指向的节点是头节点，它们之间的路径是c，而头节点有c这个路径，所以X的fail指针指向的是头节点的以c为路径的孩子节点，如图。

请添加图片描述

AC自动机的fail指针的作用

我们再来画一个图：

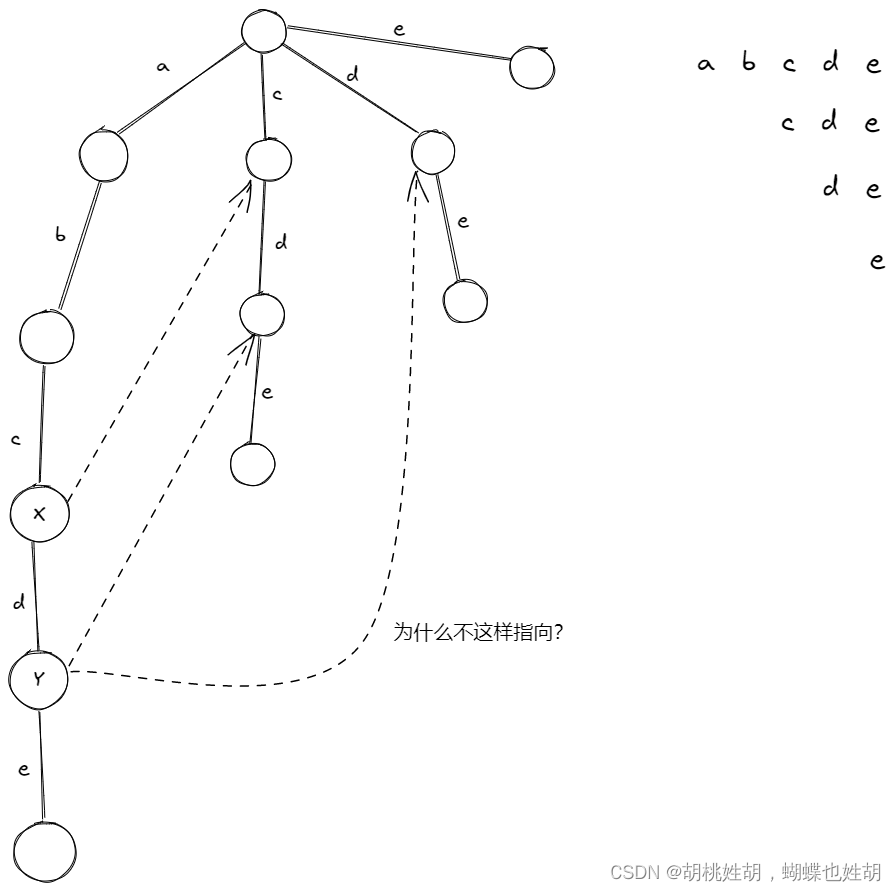
请添加图片描述

fail指针的含义比较抽象，但是我们还是尝试去概括一下：

当字符串无法匹配时，我们有最后一个字符，我们命名为last，当必须以last结尾时，与字符串拥有同一后缀的最长的字符串，fail指针的作用就是方便的找到这样一个字符串。

我们看到上图：

有节点X，假设字符串abc就是我们无法匹配成功的字符串。fail指针指向的节点和头节点连接而成的路径是c，那么这个字符串c实际上就是与abc拥有同一后缀并且最长的字符串。

在这里插入图片描述

有节点Y，假设字符串abcd就是我们无法匹配成功的字符串。Y的fail指针指向的节点与头节点连成的字符串是cd，那么cd就是与abcd拥有相同最长后缀的字符串，与abcd拥有相同后缀的字符串还有c，但是c没有cd长，所以fail指针没有指向另一头的节点。

大文章敏感词匹配

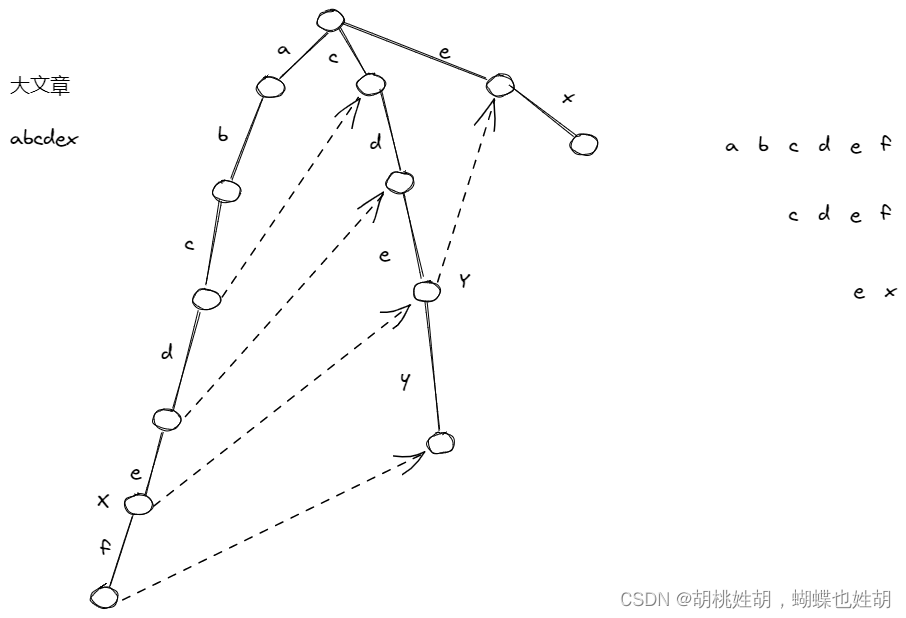
请添加图片描述

我们有大文章abcdex，我们对着这个AC自动机从0位置开始进行匹配，发现只能匹配到字符串abcde，因此得出结论，从0位置开始匹配，是无法匹配出敏感词的。
我们匹配失败了，只能匹配到字符串abcde，此时的节点是X，这时候，我们就跳往X的fail指针指向的位置的节点Y。
然后我们从头节点到Y的字符串是cde，因此，我们得到了最长的前缀保留，看，是不是跟KMP算法非常类似，AC自动机不过是在前缀树上的KMP算法。

AC自动机的代码实现

// 前缀树的节点
public class Node {
    // 如果一个 node，end为空，不是结尾
    // 如果end不为空，表示这个点是某个字符串的结尾，end的值就是这个字符串
    public String end;
    // 只有在上面的end变量不为空的时候，endUse才有意义
    // 表示，这个字符串之前有没有加入过答案, 防止答案收集重复，但是在业务场景中这个是没有必要的
    public boolean endUse;
    public Node fail;
    public Node[] nexts;

    public Node() {
        endUse = false;
        end = null;
        fail = null;
        // 这里默认是小写
        nexts = new Node[26];
    }
}

public class ACAutomation {
    private Node root;

    public ACAutomation() {
        root = new Node();
    }

    public void insert(String s) {
        char[] str = s.toCharArray();
        Node cur = root;
        int index = 0;
        for (int i = 0; i < str.length; i++) {
            index = str[i] - 'a';
            if (cur.nexts[index] == null) {
                Node next = new Node();
                cur.nexts[index] = next;
            }
            cur = cur.nexts[index];
        }
        cur.end = s;
    }

    // 宽度优先遍历
    public void build() {
        Queue<Node> queue = new LinkedList<>();
        queue.add(root);
        Node cur = null;
        Node cfail = null;
        while (!queue.isEmpty()) {
            // 当前节点弹出
            // 当前节点的所有后代加入到队列里面去
            // 当前节点给它的子去设置fail指针
            // cur -> 父亲
            cur = queue.poll();
            for (int i = 0; i < 26; i++) { // 所有的路
                if (cur.nexts[i] != null) { // 找到所有有效的路
                    // 我先设置为root，找到了就设置为别人，没找到就继续保持
                    cur.nexts[i].fail = root;
                    cfail = cur.fail;
                    while (cfail != null) {
                        if (cfail.nexts[i] != null) {
                            cur.nexts[i].fail = cfail.nexts[i];
                            break;
                        }
                        cfail = cfail.fail;
                    }
                    queue.add(cur.nexts[i]);
                }
            }
        }
    }

    // 大文章：content
    public List<String> containWords(String content) {
        char[] str = content.toCharArray();
        Node cur = root;
        Node follow = null;
        int index = 0;
        List<String> ans = new ArrayList<>();
        for (int i = 0; i < str.length; i++) {
            index = str[i] - 'a'; // 路
            // 如果当前字符在这条路上没配出来，就随着fail方向走向下条路径
            while (cur.nexts[index] == null && cur != root) {
                cur = cur.fail;
            }
            // 1) 现在来到的路径，是可以继续匹配的
            // 2) 现在来到的路径，就是前缀树的根节点
            cur = cur.nexts[index] != null ? cur.nexts[index] : root;
            follow = cur;
            // follow就是用来方便"逛"一圈儿的
            while (follow != root) {
                // 当我遇到过这个环，下次再次遇到的时候就直接break了
                if (follow.endUse) {
                    break;
                }
                // 不同的需求在这一段之间进行修改
                if (follow.end != null) {
                    ans.add(follow.end);
                    follow.endUse = true;
                }
                // 不同的需求，在这一段之间修改
                follow = follow.fail;
            }
        }
        return ans;
    }
}

我们来讲解一下void build()代码的含义：

当队列里面的节点弹出的时候，我们把这个节点的所有子节点的fail指针设置好，因为子节点的fail指针是取决于父节点的，而我们是从父节点开始遍历的，所以这个过程是父节点弹出的时候，把子节点的fail指针都设置好。
这个build代码是如何维护最长的，也就是这个代码是如何维护fail指针的正确含义的？

答：这个代码可以自动维护，不需要做其他的事情，因为这有点儿动态规划的意思，我的父亲维护的是最长的，那么我维护的就自动是最长的，而头节点是null，大概就是这样一个意思吧。

在进行匹配的时候，我们每到达一个节点，都要把这个节点的fail指针全部逛一圈，找到所有的敏感词。

        follow = cur;
        // follow就是用来方便"逛"一圈儿的
        while (follow != root) {
            // 当我遇到过这个环，下次再次遇到的时候就直接break了
            if (follow.endUse) {
                break;
            }
            // 不同的需求在这一段之间进行修改
            if (follow.end != null) {
                ans.add(follow.end);
                follow.endUse = true;
            }
            // 不同的需求，在这一段之间修改
            follow = follow.fail;
        }