目录
稳定的概念及定义:
系统稳定的充要条件——闭环极点全部落在虚轴左边:
系统的稳定性判据:
劳斯判据(充要性)判据:
劳斯表特殊情况例(出现计算过程分母为0):
劳斯表特殊情况例(出现全0行):
稳定的概念及定义:
系统在扰动作用下偏离了原来的平衡位置,当扰动消除后,系统能回到 原来的平衡位置,则称系统稳定;否则系统不稳定。
● 对线性定常系统,若其脉冲响应收敛,则系统稳定,否则不稳定
●线性定常若稳定,则原点是其唯一的平衡点,且系统一定在大 范围内渐进稳定。
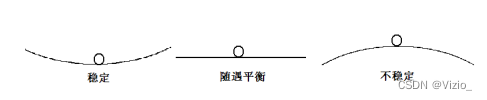
系统稳定的充要条件——闭环极点全部落在虚轴左边:

系统的稳定性判据:
高阶方程求解不易,用求特征根方法判定稳定性不现实。
![]()
必要条件:
![]() 必须有所有的ai,不能缺项
必须有所有的ai,不能缺项
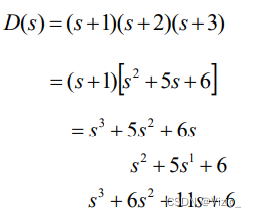
当全部根在左半 s 平面时,系数只能越加越大,不可能出现负或零。
例题:
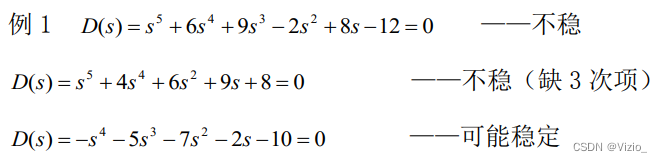
劳斯判据(充要性)判据:

劳斯表特殊情况例(出现计算过程分母为0):


劳斯表特殊情况例(出现全0行):





在虚轴上有一对复根也不稳定
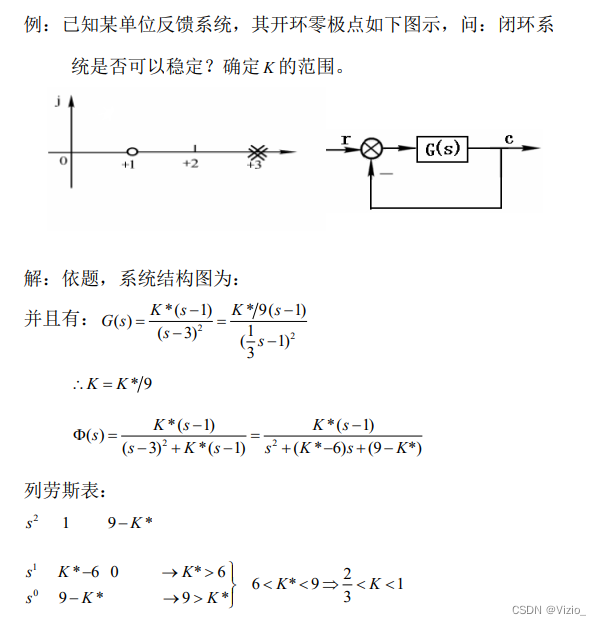

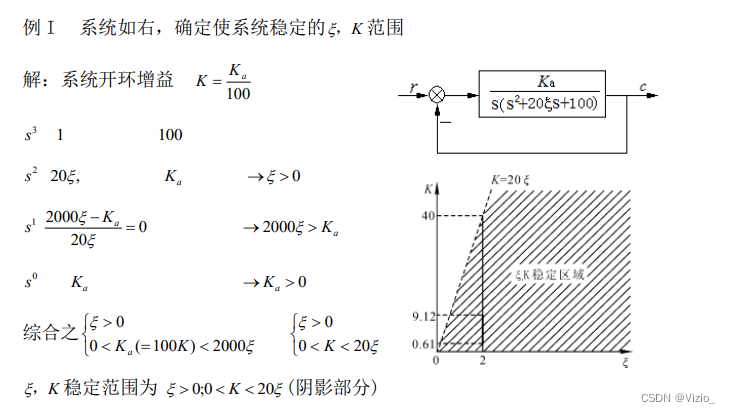
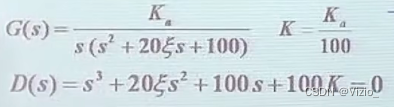
特征方程D(s)是G(s)的分母+分子(是闭环表达式的分母)

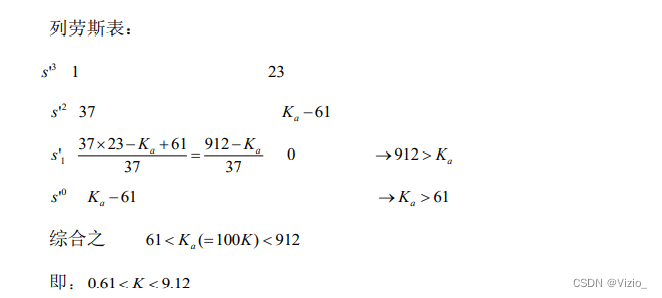
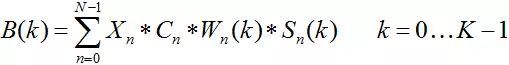









![[ CTF ] WriteUp-2022年春秋杯网络安全联赛-冬季赛](https://img-blog.csdnimg.cn/11dce9f414814cd6885b3106096842a9.png)