一.需求分析

前七个任务的解决方案，请查看上篇文章：

本文主题：基于Pandas的数据预处理技术

本次任务共分为16个任务，将其分为前七个任务和后9个任务，本文探讨其后9个任务。

本文的源代码下载链接：

基于Pandas的数据预处理技术-源代码-机器学习文档类资源-CSDN文库

https://download.csdn.net/download/weixin_52908342/87337635

本次实验内容：

1. 对第一个特征（收入中位数）排序后画散点图

2. 对第一个特征（收入中位数）画分位数图并分析

3. 【选做】对所有特征画分位数图并进行分析

4. 使用散点图、使用线性回归方法拟合第一个特征（收入中位数）并分析

5. 【选做】使用局部回归（Loess）曲线（用一条曲线拟合散点图）方法拟合第一个特征（收入中位数）数据

6. 对第一个特征（收入中位数）画分位数-分位数图并分析

7. 对第一个特征（收入中位数）画直方图，查看数据的分布和数据倾斜情况

8. 【选做】对所有特征画直方图，查看数据的分布和数据倾斜情况

9. 寻找所有特征之间的相关性并找出相关性大于 0.7 的特征对，做特征规约

二.需求解决

2.1 对第一个特征（收入中位数）排序后画散点图

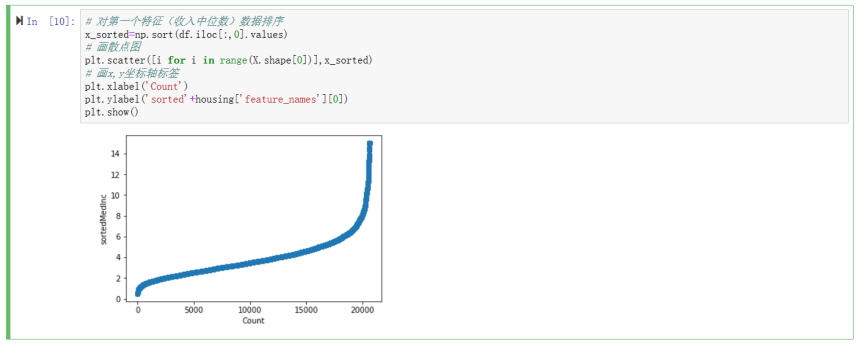
对第一个特征（收入中位数）数据排序，画散点图，画x,y坐标轴标签

x_sorted=np.sort(df.iloc[:,0].values)
plt.scatter([i for i in range(X.shape[0])],x_sorted)
plt.xlabel('Count')
plt.ylabel('sorted'+housing['feature_names'][0])
plt.show()

运行结果如下

2.2 对第一个特征（收入中位数）画分位数图并分析

对第一个特征（收入中位数）画分位数图并分析：

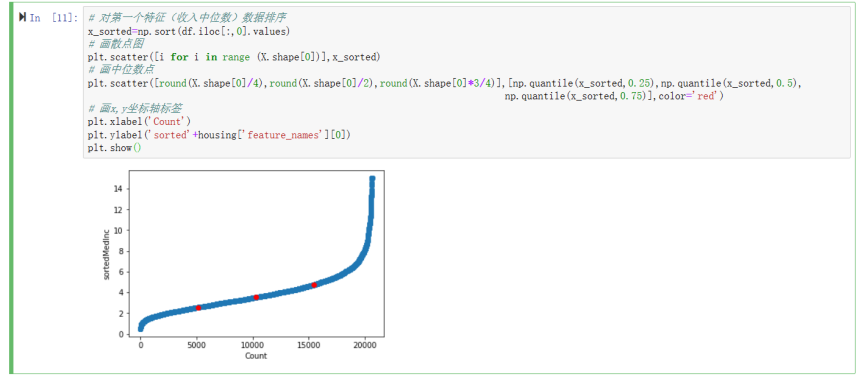
对第一个特征（收入中位数）数据排序,画散点图，画中位数点，画x,y坐标轴标签

x_sorted=np.sort(df.iloc[:,0].values)
plt.scatter([i for i in range (X.shape[0])],x_sorted)
plt.scatter([round(X.shape[0]/4),round(X.shape[0]/2),round(X.shape[0]*3/4)],[np.quantile(x_sorted,0.25),np.quantile(x_sorted,0.5),                                                                            np.quantile(x_sorted,0.75)],color='red')
plt.xlabel('Count')
plt.ylabel('sorted'+housing['feature_names'][0])
plt.show()

运行结果如下：

2.3 【选做】对所有特征画分位数图并进行分析

【选做】对所有特征画分位数图并进行分析解决方案如下：

人均收入(MedInc)、房龄(HouseAge)、房间数(AveRooms)、卧室数(AveBedrooms)、小区人口数(Population)、

房屋居住人数(AveOccup)、小区经度(Longitude)、小区纬度(Latitude)

import matplotlib.pyplot as plt
plt.figure(figsize=(12,12))
for i in range(8):
    plt.subplot(4, 2, i+1)
    # 对第一个特征（收入中位数）数据排序
    x_sorted=np.sort(df.iloc[:,i].values)
    # 画散点图
    plt.scatter([i for i in range (X.shape[0])],x_sorted)
    # 画中位数点
    plt.scatter([round(X.shape[0]/4),round(X.shape[0]/2),round(X.shape[0]*3/4)],[np.quantile(x_sorted,0.25),np.quantile(x_sorted,0.5),
                                                                                np.quantile(x_sorted,0.75)],color='red')
    # 画x,y坐标轴标签
    plt.xlabel('Count')
    plt.ylabel('sorted'+housing['feature_names'][0])
plt.show()

运行结果如下：

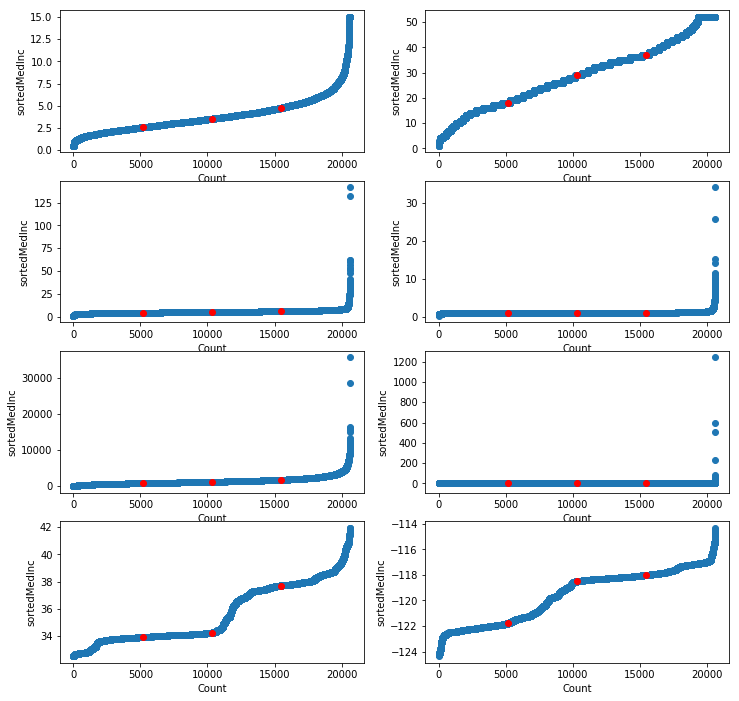
上图可以看到：8个特征的分位数图。

2.4 使用线性回归方法拟合第一个特征（收入中位数）

使用线性回归方法拟合第一个特征（收入中位数）解决方案如下：

准备数据：

X_list=[i for i in range(X.shape[0])]

转换为np.array一维向量

X_array=np.array(X_list)

转换为矩阵

X_reshape=X_array.reshape(X.shape[0],1)

对第一个特征(收入中位数)排序

x_sorted=np.sort(df.iloc[:,0].values)

线性回归

from sklearn import linear_model
linear=linear_model.LinearRegression()

进行线性回归拟合

linear.fit(X_reshape,x_sorted)

对训练结果做拟合度评分

print("training score:",linear.score(X_reshape,x_sorted))

画散点图

plt.scatter(X_list,x_sorted)

使用sklearn线性回归的predict函数计算预测值

y_predict=linear.predict(X_reshape)

画线性回归算法拟合的直线

plt.plot(X_reshape,y_predict,color='red')
plt.show()

运行结果如下：

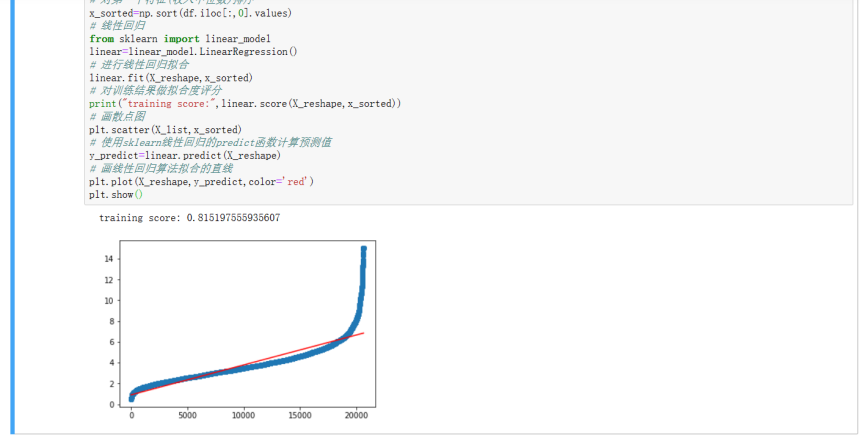
2.5 【选做】使用局部回归（Loess）曲线（用一条曲线拟合散点图）方法拟合第一个特征（收入中位数）数据

指定默认字体：解决plot不能显示中文问题,解决保存图像是负号’-'显示为方块的问题

pl.rcParams['font.sans-serif'] = ['STZhongsong']     
pl.rcParams['axes.unicode_minus'] = False           

一般来说，两个变量之间的关系非常微妙，仅用线性和曲线参数方程来描述是不够的，因此此时需要非参数回归。非参数方法和参数方法的区别在于，在分析之前预测是否存在一些限制。例如，如果我们认为特征和响应变量之间存在线性关系，我们可以使用线性方程拟合。我们只需要找到方程的系数，这是一种参数化方法，例如前面提到的线性回归和多项式回归。如果我们直接从数据中进行分析，这是一种非参数方法。因为没有限制，所以无论曲线关系如何复杂，用非参数方法拟合的曲线都能更好地描述变量之间的关系。
黄土（局部加权区域）是一种非参数的局部回归分析方法。它主要将样本划分为小单元，对区间中的样本进行多项式拟合，并重复此过程以获得不同区间中的加权回归曲线。最后，将这些回归曲线的中心连接在一起，形成一条完整的回归曲线。具体流程如下：

• 确定拟合点的数量和位置
• 以拟合点为中心确定k个最近点
• 通过权重函数计算k个点的权重
• 加权线性回归多项式拟合（一次或二次）
• 对所有拟合点重复上述步骤

import math
import numpy as np
import statsmodels.api as sm
lowess = sm.nonparametric.lowess
import pylab as pl

# 准备数据
X_list=[i for i in range(X.shape[0])]
# 转换为np.array一维向量
X_array=np.array(X_list)
# 转换为矩阵
X_reshape=X_array.reshape(X.shape[0],1)
# 对第一个特征(收入中位数)排序
x_sorted=np.sort(df.iloc[:,0].values)

yest = lowess(X_list,x_sorted, frac=0.01)[:,0]
print(yest)
# print(java1.sort)
pl.clf()
# plt.scatter(X_list,x_sorted)
plt.scatter(X_list,x_sorted,c="red", marker='o')
pl.plot(X_list, yest, label='y pred')
plt.xlabel('Count')
plt.ylabel('收入中位数')
# plt.legend(loc=1)
pl.legend()
plt.show()

运行结果如下：

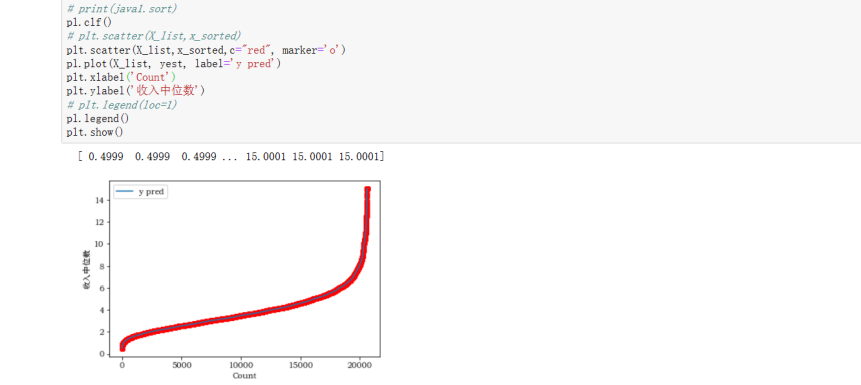
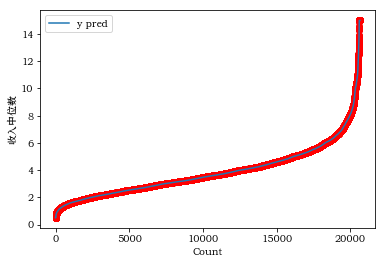
2.6 对第一个特征（收入中位数）按平均房间数分两段画分位数-分位数图并分析

对第一个特征按AveRooms平均房间数的平均值划分为两段，画分位数-分位数图:

import numpy as np
import matplotlib.pyplot as plt
plt.figure(figsize=(5,5))

对所有特征按AveRooms平均房间数的平均值划分为两段

df_new1=df[df['AveRooms']<=df['AveRooms'].mean()]
df_new2=df[df['AveRooms']>df['AveRooms'].mean()]

按照划分的两段对第一个特征排序

part1=np.sort(df_new1.iloc[:,0].values)[:df_new2['AveRooms'].count()]
part2=np.sort(df_new2.iloc[:,0].values)[:df_new2['AveRooms'].count()]

设置坐标轴刻度区间一致，画45°线

plt.xlim(part2[0],part2[-1])
plt.ylim(part2[0],part2[-1])
plt.plot([part2[0],part2[-1]],[part2[0],part2[-1]])

画分位数-分位数图

plt.scatter(part1,part2)
plt.scatter([np.quantile(part1,0.25),np.quantile(part1,0.5),np.quantile(part1,0.75)],      [np.quantile(part2,0.25),np.quantile(part2,0.5),np.quantile(part2,0.75)],color='red')
plt.show()

运行截图如下：

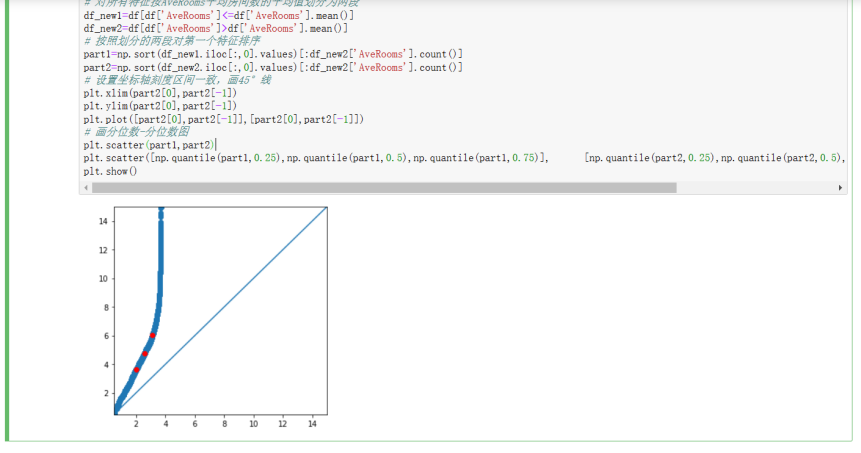
2.7 画直方图，查看各个特征的分布和数据倾斜情况

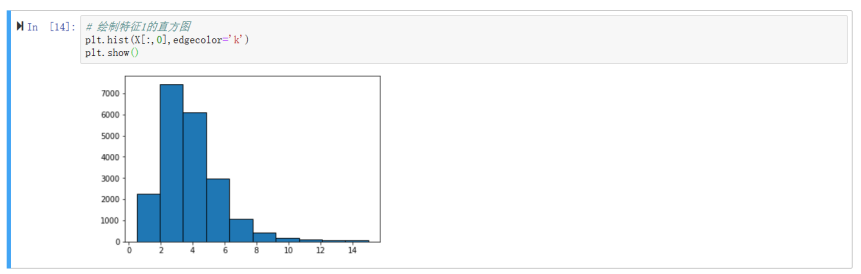
画直方图，查看各个特征的分布和数据倾斜情况。这个需求十分简单：

绘制特征1的直方图

plt.hist(X[:,0],edgecolor='k')
plt.show()

运行结果如图：

2.8 【选做】对所有特征画直方图，查看数据的分布和数据倾斜情况

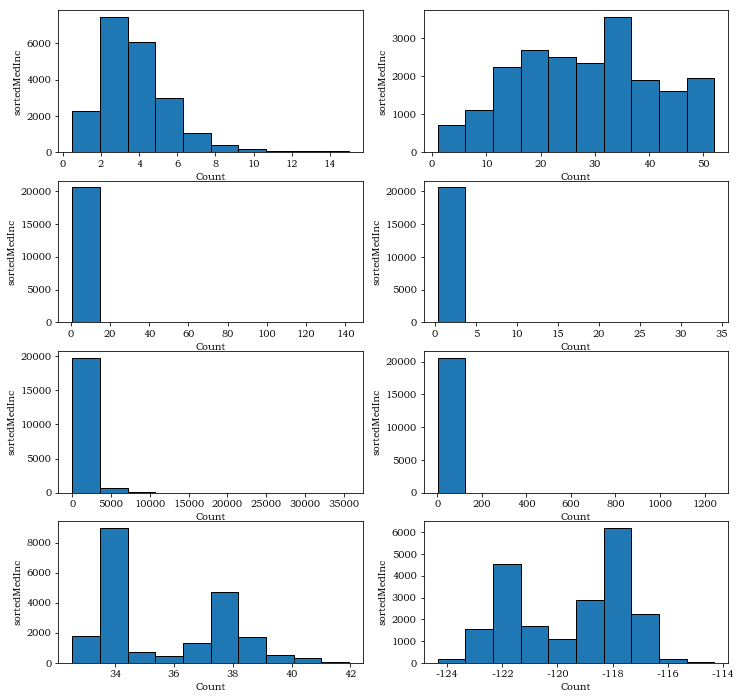
【选做】对所有特征画直方图，查看数据的分布和数据倾斜情况,需求解决方案如下：

人均收入(MedInc)、房龄(HouseAge)、房间数(AveRooms)、卧室数(AveBedrooms)、小区人口数(Population)、

房屋居住人数(AveOccup)、小区经度(Longitude)、小区纬度(Latitude)

import matplotlib.pyplot as plt
plt.figure(figsize=(12,12))
for i in range(8):
    plt.subplot(4, 2, i+1)
    plt.hist(X[:,i],edgecolor='k')
    plt.xlabel('Count')
    plt.ylabel('sorted'+housing['feature_names'][0])
plt.show()

运行结果如下：

2.9 寻找所有特征之间的相关性并找出相关性大于 0.7 的特征对，做特征规约

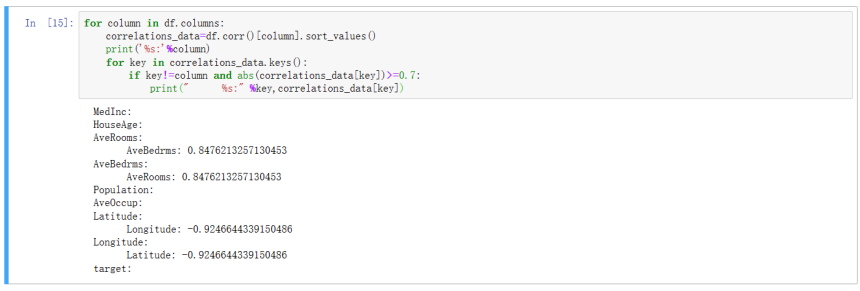
寻找所有特征之间的相关性并找出相关性大于 0.7 的特征对，做特征规约，需求解决方案如下：

for column in df.columns:
    correlations_data=df.corr()[column].sort_values()
    print('%s:'%column)
    for key in correlations_data.keys():
        if key!=column and abs(correlations_data[key])>=0.7:
            print("      %s:" %key,correlations_data[key])

运行截图如下：

2.10 总结

本次实验收获非常的大，学习到了检测是否有空值，对数据集做中心化度量，对数据集做离散化度量，包括散点图，分位数图、分位数-分位数图、包括题目要求的所有选做题目，包括局部回归的理解和使用等等，都有了较深刻的理解和运用。