1. 罗密欧与朱丽叶的迷宫问题
问题描述
罗密欧与朱丽叶的迷宫。罗密欧与朱丽叶身处一个m×n的迷宫中,如图所示。每一个方格表示迷宫中的一个房间。这m×n个房间中有一些房间是封闭的,不允许任何人进入。在迷宫中任何位置均可沿8 个方向进入未封闭的房间。罗密欧位于迷宫的(p,q)方格中,他必须找出一条通向朱丽叶所在的(r,s)方格的路。在抵达朱丽叶之前,他必须走遍所有未封闭的房间各一次,而且要使到达朱丽叶的转弯次数为最少。每改变一次前进方向算作转弯一次。请设计一个算法帮助罗密欧找出这样一条道路。
编程任务:
对于给定的罗密欧与朱丽叶的迷宫,编程计算罗密欧通向朱丽叶的所有最少转弯道路。
数据输入:
输入第一行有3个正整数n,m,k,分别表示迷宫的行数,列数和封闭的房间数。接下来的k行中,每行2个正整数,表示被封闭的房间所在的行号和列号。最后的2 行,每行也有2 个正整数,分别表示罗密欧所处的方格(p,q)和朱丽叶所处的方格(r,s)。
结果输出:
输出计算出的罗密欧通向朱丽叶的最少转弯次数和有多少条不同的最少转弯道路。输出的第1行是最少转弯次数。输出的第2行是不同的最少转弯道路数。接下来的n行每行m个数,表示迷宫的一条最少转弯道路。A[i][j]=k表示第k步到达方格(i,j);A[i][j]=-1 表示方格(i,j)是封闭的。
如果罗密欧无法通向朱丽叶则输出“No Solution!”。
输入示例
3 4 2
1 2
3 4
1 1
2 2
输出示例
6
7
1 -1 9 8
2 10 6 7
3 4 5 -1
#include<bits/stdc++.h>
using namespace std;
/*
3 4 2
1 2
3 4
1 1
2 2
*/
int m,n,k;
int p,q,r,s;
int ans[1010][1010],a[1010][1010];
int dx[8]={0,1,1,1,0,-1,-1,-1},
dy[8]={1,1,0,-1,-1,-1,0,1};
int minas=1e8+10,flag=0,anslu=0;
//最少转弯次数,判断是否有答案,最少转弯次数的数量
void dfs(int x,int y,int num,int turn,int dir)
{
if(x==r && y==s && turn<=minas && num==n*m-k)
{
if(turn<minas)
{
minas=turn;
anslu=1;
flag=1;
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
ans[i][j]=a[i][j];
}
}
}
else
{
anslu++;
}
return ;
}
for(int i=0;i<8;i++)
{
int xx=x+dx[i],yy=y+dy[i];
if(xx<1 || xx>m || yy<1 || yy>n) continue;
if(a[xx][yy]!=0) continue;
a[xx][yy]=num+1;
if(dir!=i)
{
if(turn+1<=minas)
{
dfs(xx,yy,num+1,turn+1,i);
}
}
else//相同方向
{
dfs(xx,yy,num+1,turn,i);
}
a[xx][yy]=0;
}
}
int main()
{
cin>>m>>n>>k;
for(int i=1;i<=k;i++)
{
int x,y;
cin>>x>>y;
a[x][y]=-1;
}
cin>>p>>q>>r>>s;
a[p][q]=1;
dfs(p,q,1,-1,8);
if(flag==1)
{
cout<<minas<<endl<<anslu<<endl;
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
cout << ans[i][j]<<" ";
}
cout << endl;
}
}
else
{
cout << "No Solution!\n";
}
return 0;
}
2. n色方柱问题
问题描述
设有 n 个立方体,每个立方体的每一面用红、黄、蓝、绿等 n 种颜色之一染色。要把这n 个立方体叠成一个方形柱体,使得柱体的 4 个侧面的每一侧均有 n 种不同的颜色。试设计一个回溯算法,计算出 n 个立方体的一种满足要求的叠置方案。
对于给定的 n 个立方体以及每个立方体各面的颜色,计算出 n 个立方体的一种叠置方案,使得柱体的 4 个侧面的每一侧均有 n 种不同的颜色。
数据输入:
第一行有 1 个正整数 n,0< n< 27,表示给定的立方体个 数和颜色数均为 n。第 2 行是 n 个大写英文字母组成的字符串。该字符串的第 k(0≤ k< n) 个字符代表第 k 种颜色。接下来的 n 行中,每行有 6 个数,表示立方体各面的颜色。立方体各面的编号如下图所示。
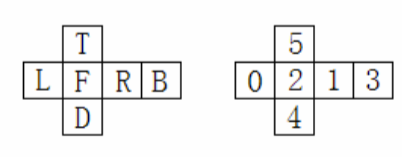
图中 F 表示前面,B 表示背面,L 表示左面,R 表示右面,T 表示顶面,D 表示底面。相应地,2 表示前面,3 表示背面,0 表示左面,1 表示右面,5 表示顶面,4 表示底面。
结果输出:
输出n个立方体的一种可行的叠置方案。每行 6 个字符,表示立方体个面的颜色。如果不存在所要求的叠置方案,输出 “No Solution”
输入示例:
4
RGBY
0 2 1 3 0 0
3 0 2 1 0 1
2 1 0 2 1 3
1 3 3 0 2 2
输出示例:
RBGYRR
YRBGRG
BGRBGY
GYYRBB
#include<bits/stdc++.h>
using namespace std;
int n;
string s;
char t[1010];
int main()
{
cin>>n;
cin>>s;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=6;j++)
{
int k;
cin>>k;
cout << s[k];
}
cout << endl;
}
return 0;
}3. 最佳调度问题
问题描述:
假设有 n 个任务由 k 个可并行工作的机器来完成。完成任务 i 需要时间为ti ,设计完成这 n 个任务的最佳调度算法,使得完成全部任务的时间最早。
编程任务:
对任意给定的整数n和k,以及完成任务i需要的时间为ti,i=1,2,…,n。编程计算完成这n个任务的最佳调度。
输入样例:(第一行为任务数n,第二行为可并行工作的机器数k,第三行为机器完成任务i所需的单位时间)
10
7
67 45 80 32 59 95 37 46 28 20
输出样例:(第一行是完成所有任务的最优化时间)
95
#include<bits/stdc++.h>
using namespace std;
/*
10
7
67 45 80 32 59 95 37 46 28 20
*/
int n,k,a[1010]={0},b[1010]={0},maxx=1e8;
void dfs(int x,int t)
{
if(t>=maxx)
{
return ;
}
if(!x)
{
maxx=t;
return ;
}
bool vis[1010]={0};
for(int i=1;i<=k;i++)
{
if(vis[b[i]]) continue;
vis[b[i]]=true;
b[i]+=a[x];
dfs(x-1,max(t,b[i]));
b[i]-=a[x];
}
return ;
}
int main()
{
cin>>n>>k;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
sort(a+1,a+n+1);
dfs(n,0);
cout << maxx<<endl;
return 0;
}4. 运动员最佳匹配问题
问题描述:
羽毛球队有男女运动员各n 人。给定2 个n×n 矩阵P 和Q。P[i][j]是男运动员i 和女运动员j配对组成混合双打的男运动员竞赛优势;Q[i][j]是女运动员i和男运动员j配合的女运动员竞赛优势。由于技术配合和心理状态等各种因素影响,P[i][j]不一定等于Q[j][i]。男运动员i和女运动员j配对组成混合双打的男女双方竞赛优势为P[i][j]*Q[j][i]。设计一个算法,对于给定的男女运动员竞赛优势,计算男女运动员最佳配对法,使各组男女双方竞赛优势的总和达到最大。
编程任务:
给定2 个n×n 矩阵P 和Q。P[i][j]是男运动员i 和女运动员j配对组成混合双打的男运动员竞赛优势;Q[i][j]是女运动员i和男运动员j配合的女运动员竞赛优势。设计一个算法,对于给定的男女运动员竞赛优势,计算男女运动员最佳配对法,使得
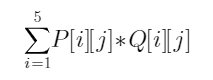
()的值最大化。并输出最大值。
输入样例:(第一行是男队员(或女队员)的个数,第二、三、四行是男运动员i 和女运动员j配对组成混合双打的男运动员竞赛优势,第五、六、七行是女运动员i和男运动员j配合的女运动员竞赛优势)
3
10 2 3
2 3 4
3 4 5
2 2 2
3 5 3
4 5 1
输出样例:(第一行是竞赛优势的最大和)
52
#include<bits/stdc++.h>
using namespace std;
/*
3
10 2 3
2 3 4
3 4 5
2 2 2
3 5 3
4 5 1
*/
int n;
int p[30][30],q[30][30],s[30],maxx=0;
bool vis[30];
void dfs(int x,int summ)
{
if(x>n)
{
maxx=max(summ,maxx);
}
for(int i=1;i<=n;i++)
{
if(!vis[i])
{
vis[i]=1;
dfs(x+1,summ+p[x][i]*q[i][x]);
vis[i]=0;
}
}
}
int main()
{
cin>>n;
for(int i=1; i<=n; i++)
{
for(int j=1; j<=n; j++)
{
cin>>p[i][j];
}
}
for(int i=1; i<=n; i++)
{
for(int j=1; j<=n; j++)
{
cin>>q[i][j];
}
}
dfs(1,0);
cout << maxx<<endl;
return 0;
}