(一) 相关知识点
图(graph):图是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中的顶点的集合,E是图G中边的集合,E可以为空集。
数据结构形式化定义:
G = ( V , E ) 其中 V = { x | x dataobject } E ={VR}
VR={<x,y>| p(x,y) ∩ ( x , y∈V ) }
VR是两顶点间的关系的集合,即边的集合。
顶点(Vertex):图中的数据元素。线性表中数据元素叫元素,树中数据元素叫结点。
端点和邻接点: 在一个无向图中,若存在一条边<vi,vj>, 则称vi,vj为该边的两个端点,并称它们互为邻结点。
起点和终点 :在一个有向图中,若存在一条边<vi,vj>, 则称该边是顶点vi的一条出边, 是vj的一条入边,称vi是起始端点(或起点),称vj是终止端点(或终点), 并称它们互为邻结点.
边:顶点之间的逻辑关系用边来表示,边集可以是空的。
无向边(Edge):若顶点V1到V2之间的边没有方向,则称这条边为无向边。
边和顶点的关系:
设n为顶点数,e为边或弧的条数 对无向图有:0 ≤ e ≤ n(n-1)/2 有向图有:0≤ e ≤ n(n-1)
无向图(Undirected graphs):图中任意两个顶点之间的边都是无向边。 (A,D)=(D,A)
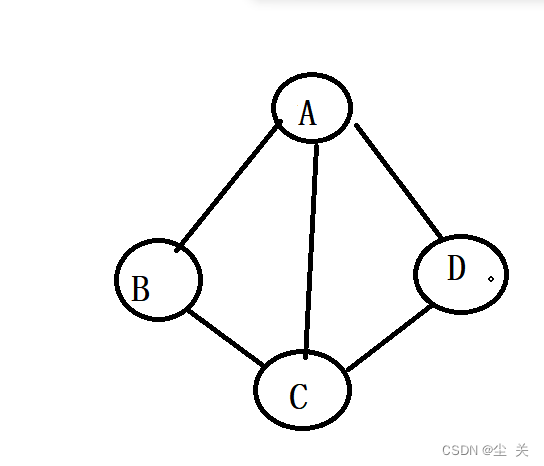
对于无向图G来说,G1=(V1,{E1}),其中顶点集合V1={A,B,C,D};边集和E1={(A,B),(B,C),(C,D),(D,A),(A,C)} 注意:无向边用“()”,而有向边用“< >”表示。
有向边:若从顶点V1到V2的边有方向,则称这条边为有向边,也称弧(Arc)。用<V1,V2>表示,V1为弧尾(Tail)(箭尾为尾),V2为弧头(Head)(箭头为弧头) 注意:(V1,V2)≠(V2,V1)
有向图(Directed graphs):图中任意两个顶点之间的边都是有向边。
简单图:图中不存在顶点到其自身的边,且同一条边不重复出现(没有自环和不含多重边)。
完全图:每对顶点之间都恰连有一条边的图
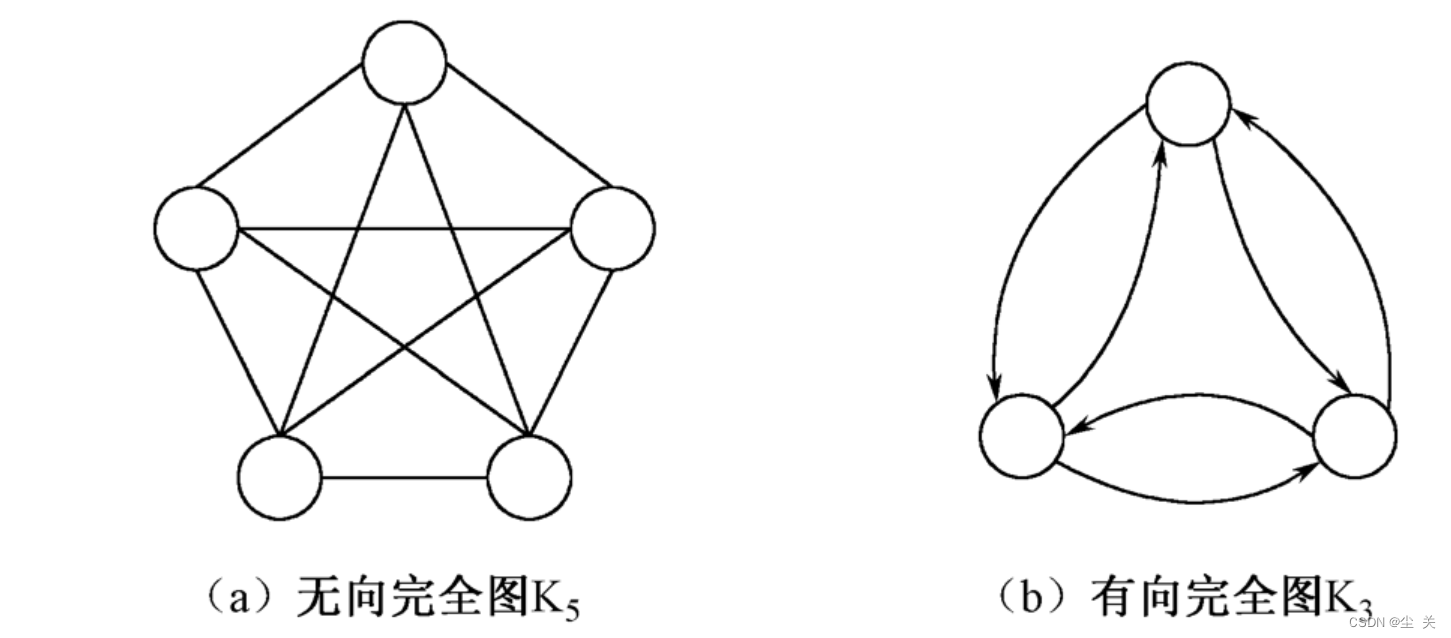
无向完全图:无向图中,任意两个顶点之间都存在边。
有向完全图:有向图中,任意两个顶点之间都存在方向互为相反的两条弧。
稀疏图:有很少条边。
稠密图:有很多条边。
权(Weight):与图的边或弧相关的数。
网(Network):带权的图。
子图(Subgraph):假设G=(V,{E})和G‘=(V',{E'}),如果V'包含于V且E'包含于E,则称G'为G的子图。
度(Degree):无向图中,与顶点V相关联的边的数目。有向图中,入度表示指向自己的边的数目,出度表示指向其他边的数目,该顶点的度等于入度与出度的和。
路径 非空有限点、弧交替序列, W=v0, a1,v1, … , ak,vk 使得i=1,2,…k , 弧ai的头vi , 尾为vi-1 。
简单路径:除首尾两点外,其他各点都不相同的路径称为简单路径。
回路:无重复边的闭路径。
环:闭的简单路径,称为环。
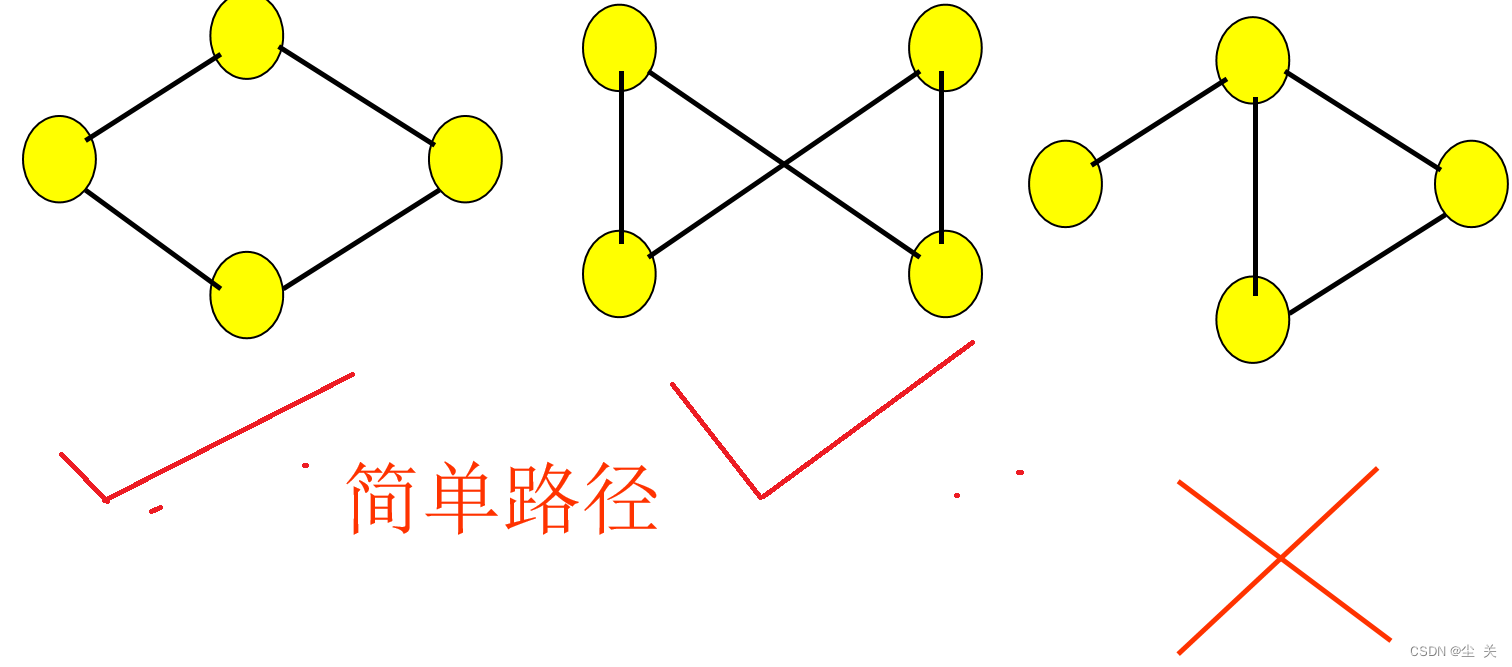
路径的长度:一条路径上边或弧的数量。
连通图:图中任意两个顶点都是连通的。
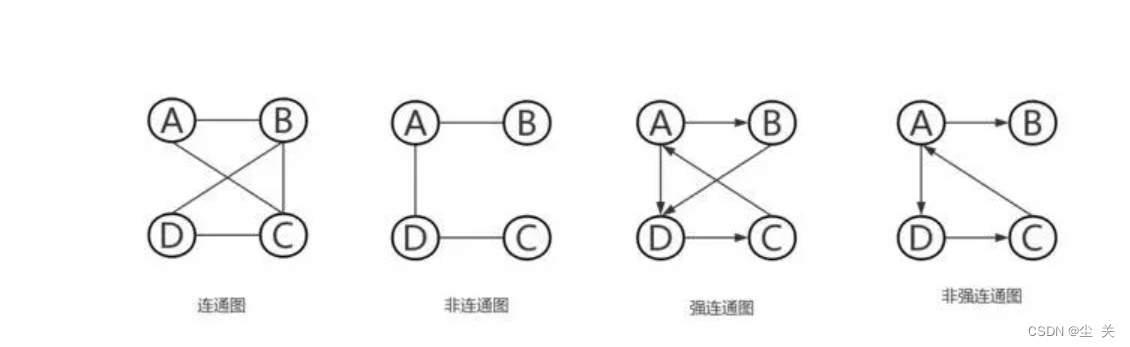
连通分量:无向图中的极大连通子图。(子图必须是连通的且含有极大顶点数)。图1有两个连通分量
强连通分量:有向图中的极大强连通子图。
(二)图的存储结构
图有两种存储结构分别为矩阵法和邻接表。
矩阵法
#include <stdio.h>
#include <malloc.h>
#define INF 32767 //定义正无穷
#define MAXV 100//最大顶点数
typedef char InfoType;
//定义邻接矩阵
typedef struct
{
int no;//顶点编号
InfoType info;//顶点其他信息
}Vertextype;//顶点类型
typedef struct
{
int edges[MAXV][MAXV];//邻接矩阵数组
int n, e;//顶点数、边数
Vertextype vexs[MAXV];//存放顶点信息
}MatGraph; //完整的图邻接矩阵类型
//邻接矩阵的基本运算算法
void CreateMat(MatGraph& g, int A[MAXV][MAXV], int n, int e)
{
int i, j;
g.n = n; g.e = e;
for ( i = 0; i < g.n; i++)
{
for (j = 0; j < g.n; j++) {
g.edges[i][j] = A[i][j];
}
}
}
void DispMat(MatGraph g)
{
int i, j;
for (i = 0; i < g.n; i++)
{
for (j = 0; j < g.n; j++) {
if (g.edges[i][j] != INF)
printf("%4d", g.edges[i][j]);
else
{
printf("%4s","∞");
}
}
puts("\n");
}
}
int main()
{
MatGraph g;
int A[MAXV][MAXV] = {
{0,5,INF,7,INF,INF},{INF,0,4,INF,INF,INF},{8,INF,0,INF,INF,9},{INF,INF,5,0,INF,6},
{INF,INF,INF,5,0,INF},{3,INF,INF,INF,1,0}
};
int n = 6, e = 10;
CreateMat(g, A, n, e);
printf("邻接矩阵运算:\n"); DispMat(g);
return 0;
}
领接表
#include <stdio.h>
#include <malloc.h>
#define INF 32767 //定义正无穷
#define MAXV 100//定义最大顶点个数
typedef char InfoType;
//定义邻接表类型
typedef struct ANode
{
int adjvex;//该边的邻接点的编号
struct ANode* nextarc;//指向下一条边的指针
int weight;//该边的权值
}ArcNode;
typedef struct Vnode
{
InfoType info;//顶点其他信息
int count;//存放顶点入度,仅用于拓扑排序
ArcNode* firstarc;//指向第一条边
}VNode;
typedef struct
{
VNode adjlist[MAXV];//邻接表头结点数组
int n, e;//图中顶点数n和边数e
}AdjGraph;
//邻接表的基本运算算法
void CreateAdj(AdjGraph *&G, int A[MAXV][MAXV], int n, int e)
{
int i, j;
ArcNode* p;
G = (AdjGraph*)malloc(sizeof(AdjGraph));
for (int i = 0; i < n; i++)
{
G->adjlist[i].firstarc = NULL;
}
for ( i = 0; i < n; i++)
{
for (j = n - 1; j >= 0; j--) {
if (A[i][j] != 0 && A[i][j] != INF)
{
p = (ArcNode*)malloc(sizeof(ArcNode));
p->adjvex = j;
p->weight = A[i][j];
p->nextarc = G->adjlist[i].firstarc;
G->adjlist[i].firstarc = p;
}
}
}
G->n = n; G->e = e;
}
void DispAdj(AdjGraph* G )
{
ArcNode* p;
for (int i = 0; i < G->n; i++)
{
p = G->adjlist[i].firstarc;
printf("%3d", i);
while (p != NULL)
{
printf("%3d[%d]->", p->adjvex, p->weight);
p = p->nextarc;
}
printf("▽\n");
}
}
void DestroyAdj(AdjGraph*& G)
{
ArcNode* pre, * p;
for (int i = 0; i < G->n; i++)
{
pre= G->adjlist[i].firstarc;//
if (pre != NULL)
{
p = pre->nextarc;
while (p != NULL)
{
free(pre);
pre = p;
p = p->nextarc;
}
free(pre);
}
}
free(G);
}
int main()
{
AdjGraph* G;
int A[MAXV][MAXV] = {
{0,5,INF,7,INF,INF},{INF,0,4,INF,INF,INF},{8,INF,0,INF,INF,9},{INF,INF,5,0,INF,6},
{INF,INF,INF,5,0,INF},{3,INF,INF,INF,1,0}
};
int n = 6, e = 10;
CreateAdj(G, A, n, e);
printf("邻接表运算:\n"); DispAdj(G);
DestroyAdj(G);
return 0;
}