剑指offer --- 二维数组中的元素查找

news2024/10/6 14:24:32

一、读懂题目

二、思路分析

三、代码呈现

总结

一、读懂题目

题目：

在一个二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的个二维数组和一个整数，判断数组中是否含有该整数。

首先我们分析由于该二维数组有序，且呈现从上到下、从左到右递增的规律，比如该示例：

我们需要从中找出输入数是否存在，如果存在返回true，反之返回false即可。

二、思路分析

当然在非大数问题的案例而言，我们完全可以使用逐层逐位遍历的方式寻找是否有值存在，但是如果数组行列数比较大时，这种方法的效率是极其有限的。既然题中指出存在横纵两方向的递增规律，那么我们只需要从这部分下手即可降低时间复杂度，减少程序的运行时间。

现假设我们需要查找数字 7 是否位于数组中，有以下思路：

首先我们选取数组右上角的数字 9。由于 9 大于 7，并且 9 还是第 4 列的第一个（也是最小的）数字，因此 7 不可能出现在数字 9 所在的列。于是我们把这一列从需要考虑的区域内剔除，之后只需要分析剩下的 3 列。

在剩下的矩阵中，位于右上角的数字是 8。同样 8 大于 7，因此 8 所在的列我们也可以剔除。接下来我们只要分析剩下的两列即可。

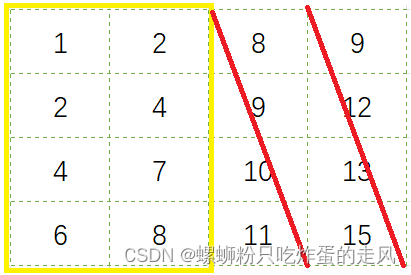
在由剩余的两列组成的数组中,数字 2 位于数组的右上角。2 小于 7，那么要查找的 7 可能在 2 的右边，也有可能在 2 的下边。在前面的步骤中，我们已经发现 2 右边的列都已经被剔除了，也就是说 7 不可能出现在 2 的右边，因此 7 只有可能出现在 2 的下边。于是我们把数字 2 所在的行也剔除，只分析剩下的三行两列数字。

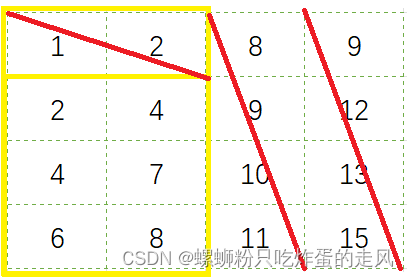
在乘下的数字中，数字 4 位于右上角，和前面一样，我们把数字 4 所在的行也删除，最后剩下两行两列数字。

在剩下的两行两列矩阵中，因为右上角已经是 index = 7 的值，所以直接返回 true 表示查找成功即可。通过上面的分析，我们不难写出代码，当然理应从代码的鲁棒性出发，特别注意对特殊情况的处理。

正常输入情况：

1. 二维数组中包含查找的数字 (查找的数字是数组中的最大值和最小值，查找的数字介于数组中的最大值和最小值之间)。
2. 二维数组中没有查找的数字 (查找的数字大于数组中的最大值，查找的数字小于数组中的最小值，查找的数字在数组的最大值和最小值之间但数组中没有这个数字)。

特殊输入测试：

输入空指针。

三、代码呈现

利用数组下标访问实现：

template<typename T>
bool find_num(const T** arr_2, size_t row, size_t col, const T target)
{
	if (arr_2 == nullptr || row <= 0 || col <= 0)
	{
		throw exception("find_num:: the input parameters do not meet the requirements");
	}

	int left = 0;			// 控制行舍去
	int right = col - 1;	// 控制列舍去

	while (left < row && right > 0)
	{
		if (arr_2[left][right] == target) { return true; }
		if (arr_2[left][right] > target)	// 向左遍历求更小值
		{
			right--;
		}
		if (arr_2[left][right] < target)	// 向下遍历求更大值
		{
			left++;
		}
	}
	return false;
}

测试方法一：

当我们需要调用此方法验证时，需要传入动态数组的二阶指针以符合函数参数列表要求，如下：

void test1_1()
{
	int* arr[] = 
    {
	    new int[4] {1,2,8,9},
	    new int[4] {2,4,9,12},
	    new int[4] {4,7,10,13},
	    new int[4] {6,8,11,15}
	};
	int target = 7;

	try
	{
        // 使用const_cast修改的效果仅在转换语句行有效，不会真正改变对象的常量性
		bool ret = find_num<int>(reinterpret_cast<const int**>(const_cast<const int**>(arr)), 
                sizeof(arr) / sizeof(arr[0]), sizeof(arr[0]) / sizeof(arr[0][0]), target);
		if (ret == true) { cout << "已找到！" << endl; }
		else { cout << "未找到" << endl; }
	}
	catch (const exception& e)
	{
		cout << e.what() << endl;
	}
	catch (...)
	{
		cout << "other default!" << endl;
	}
    
    // 释放堆区空间
    for (int i = 0; i < 4; i++)
    {
	    delete[] arr[i];
	    arr[i] = nullptr;
    }
}

运行结果：

利用指针偏移访问实现：

测试方法二：

出于我们用到的静态数组所占比例大多数情况不比动态数组少，所以最好还得想想办法解决静态二维数组传参的问题，因为考虑到二维数组在内存中是连续存放的，每行以 “Z” 字形被连续存放在内存中，所以可以在该函数功能内直接将其看作一维数组处理，由于传入的指针是二阶指针，所以将其类型强转为一阶指针，再利用指针偏移来访问各个元素即可。来看代码：

函数实现部分：

// 利用指针访问元素
template<typename T>
bool find_num_ptr(const T** arr, size_t row, size_t col, const T target)
{
	if (arr == nullptr || row <= 0 || col <= 0)
	{
		throw exception("find_num:: the input parameters do not meet the requirements");
	}

	const T* arr_2 = reinterpret_cast<T*>(arr);  // 注意强转指针部分
	int left = 0;			// 控制行舍去
	int right = col - 1;	// 控制列舍去

	while (left < row && right > 0)
	{
		if (*(arr_2 + left * col + right) == target) { return true; }
		if (*(arr_2 + left * col + right) > target)	// 向左遍历求更小值
		{
			right--;
		}
		if (*(arr_2 + left * col + right) < target)	// 向下遍历求更大值
		{
			left++;
		}
	}
	return false;
}

测试函数功能部分（传入静态数组）：

void test1_2()
{
	int arr[4][4] =
	{
		{1,2,8,9},
		{2,4,9,12},
		{4,7,10,13},
		{6,8,11,15}
	};

	int target = 7;
	try
	{
        // 正常将二维数组名强转为二阶指针（函数功能内部再将其转换为一阶指针进行元素访问）
		bool ret = find_num_ptr<int>(reinterpret_cast<const int**>(arr), 
									sizeof(arr) / sizeof(arr[0]), 
									sizeof(arr[0]) / sizeof(arr[0][0]), 
									target);
		if (ret == true) { cout << "已找到！" << endl; }
		else { cout << "未找到" << endl; }
	}
	catch (const exception& e)
	{
		cout << e.what() << endl;
	}
	catch (...)
	{
		cout << "other default!" << endl;
	}
}

运行结果：