分析

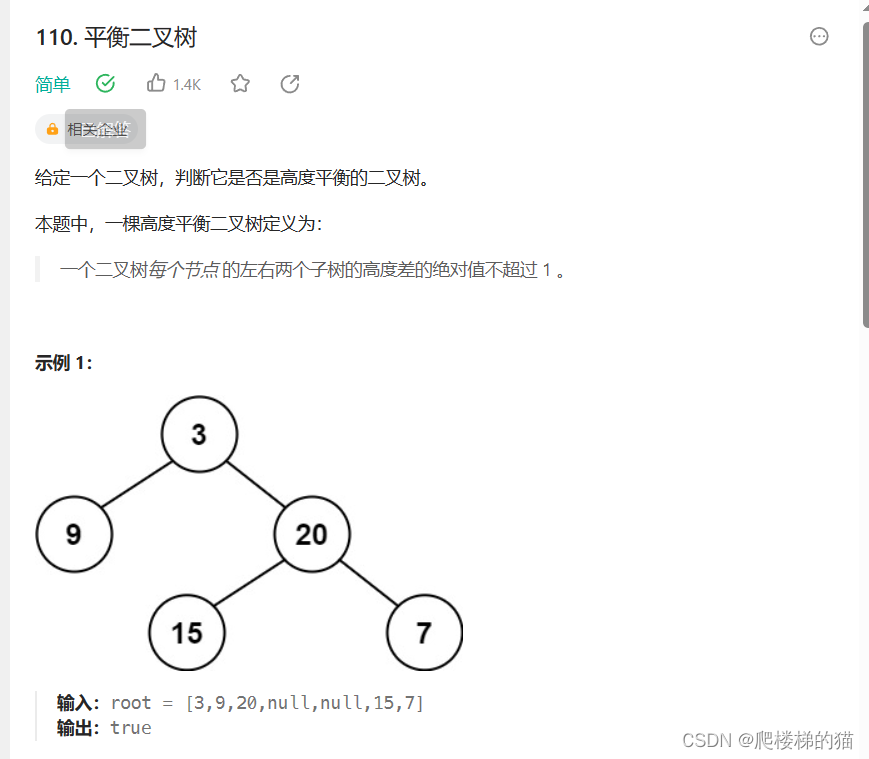
根据平衡二叉树的定义，只需要满足：1、根节点两个子树的高度差不超过1；2、左右子树都为平衡二叉树

代码

public class BalancedBinaryTree {
    public class TreeNode{
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode(){}
        TreeNode(int val){
            this.val = val;
        }
    }
    public boolean isBalanced(TreeNode root) {
        if(root == null){
            return true;
        }
        //判断左子树是否为平衡二叉树
        int leftH = getHeight(root.left);
        //判断右子树是否为平衡二叉树
        int rightH = getHeight(root.right);
        //当满足三个条件时返回ture
        return Math.abs(leftH-rightH)<2&&isBalanced(root.left)&&isBalanced(root.right);
    }
    //获取树的高度
    public int getHeight(TreeNode root){
        if(root == null){
            return 0;
        }
        //获取左子树高度
        int leftH = getHeight(root.left);
        //获取右子树高度
        int rightH = getHeight(root.right);
        //返回左右子树的最大值+1（加上根节点高度），即为树的高度
        return ((leftH > rightH) ? (leftH+1):(rightH+1));
    }
}

进行优化

但是这样的做法，每对一个结点进行平衡判定就要求一次 以该结点为根节点的树的高度。时间复杂度太大

所以我们在求高度的时候就进行判定是否平衡。 

---

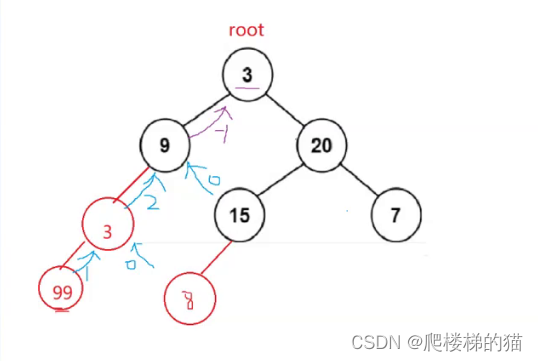
在求高度的时候就进行平衡判定，如果其中一颗子树不平衡，就直接返回-1（因为高度是不能为-1的），子树为空则返回0。

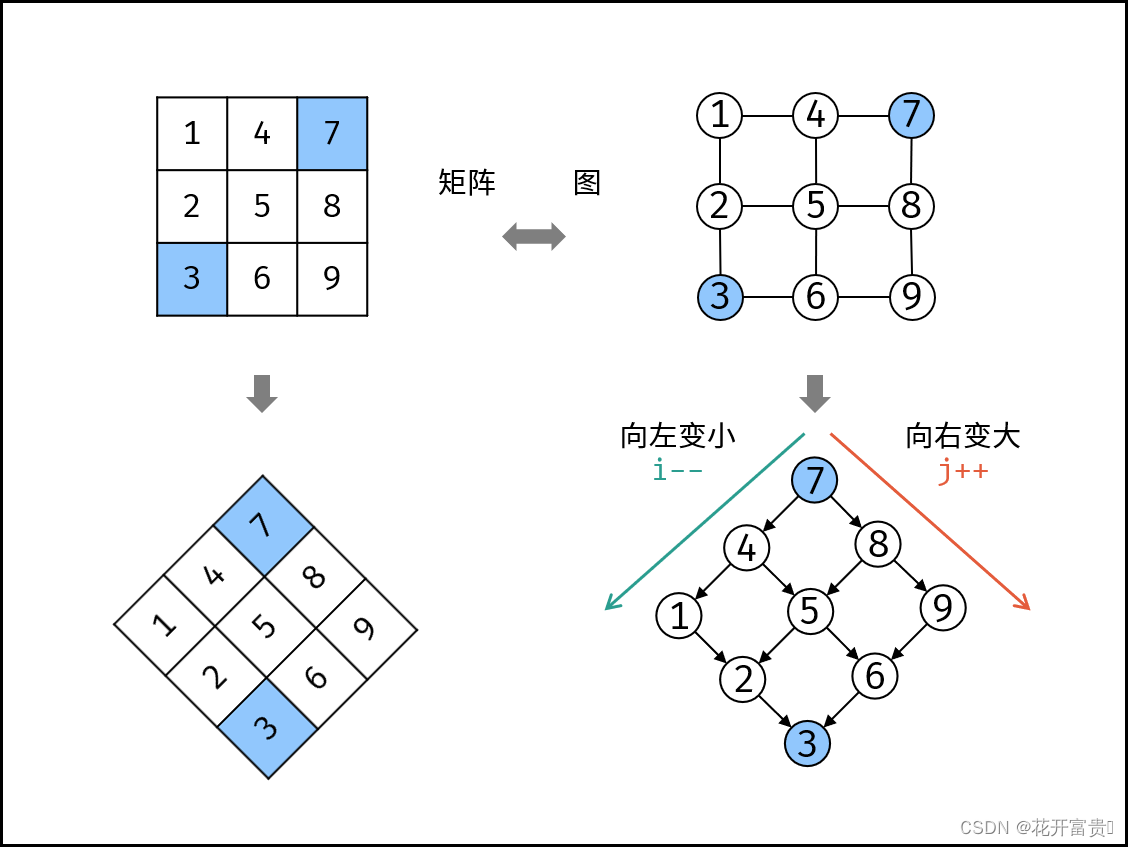
如下图所示。对于3为根节点的二叉树，左树返回1，右树返回0；然后对于9为根节点的二叉树，左子树返回2，右子树返回0；对于以3为根节点的二叉树，左子树返回-1（说明左子树不平衡），右子树返回-1（说明右子树不平衡），所以以3为根节点的二叉树返回-1.

同时要注意：存在一个根节点，其左子树不平衡返回-1，右子树为空返回0，但此时左右子树高度差的绝对值还是1.所以我们要对此做出限制

 优化后的代码

public class Test3 {
    public class TreeNode{
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode(){}
        TreeNode(int val){
            this.val = val;
        }
    }
    public boolean isBalanced(TreeNode root) {
        return getHeight(root) >= 0;
    }
    //获取树的高度
    public int getHeight(TreeNode root){
        if(root == null){
            return 0;
        }
        //获取左子树高度
        int leftH = getHeight(root.left);
        //获取右子树高度
        int rightH = getHeight(root.right);
        /*如果一个节点左树不平衡（返回-1），右树为空（返回0）。它不是个平衡二叉树，但是它满足左右子树高度差为1
        * 所以这里限制左右子树高度都大于0*/
        if (leftH >= 0 && rightH >= 0 &&
        Math.abs(leftH - rightH)<=1){
            return Math.max(leftH,rightH)+1;
        }else {
            return -1;
        }
        /*为什么不能在第一个不平衡的二叉树出现时就结束？
        * 因为你是判断高度的方法，不是判断平衡的方法。
        * false应该在另一个方法中被返回*/
    }
}