---

二叉树

---

一、树的概念

1.树形结构

1.1. 树的特点：

1.根节点没有前驱节点
2.除根节点外，其余结点分成了M个互不相交的集合
3.子树的根节点有且只有一个前驱
4.树是递归定义的

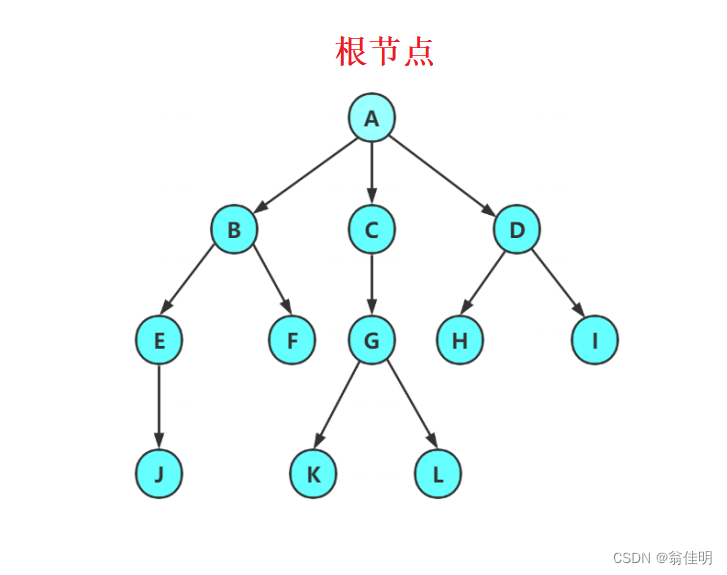
• 树形结构中，子树不能相交；
• 除了根节点外，每个结点有且只有一个父结点；
• 一颗N个结点的树，有N-1条边；

1.2 概念：

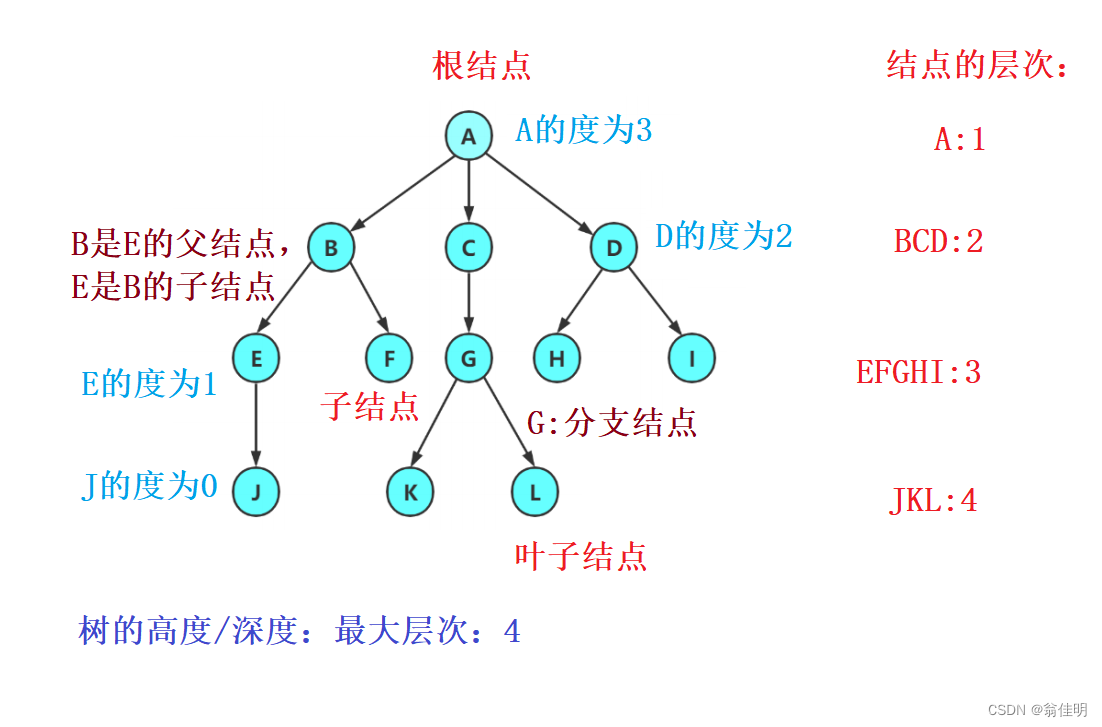
• 1.结点的度：一个结点含子树的个数 ，如上图：A的度为3；
• 2.树的度：树中，结点的度最大值 ，数的度为3 ；
• 3.叶子结点/终端结点：度为0的结点（没有子结点）如J、F、K、L、H、I；
• 4.父结点/双亲节点：含有子节点的结点. 如A是C的父结点；
• 5.子结点/孩子结点：如B是A的子结点
• 6.根结点：一棵树中，没有父结点的结点： A
• 7.结点的层次：从根结点开始，根为第1层，根的子结点为第2层…
• 8.树的高度/深度:树中结点的最大层次。 上图中树的高度为4；
• 9.分支结点/非终端结点：度不为0的结点：E,G…
• 10.兄弟结点：具有相同的父结点：E、F
• 11.堂兄弟结点：其父结点都在同一层；F、G
• 12.森林:多棵互不相交的的数的结合

1.3 树的表示形式

孩子兄弟表示法：

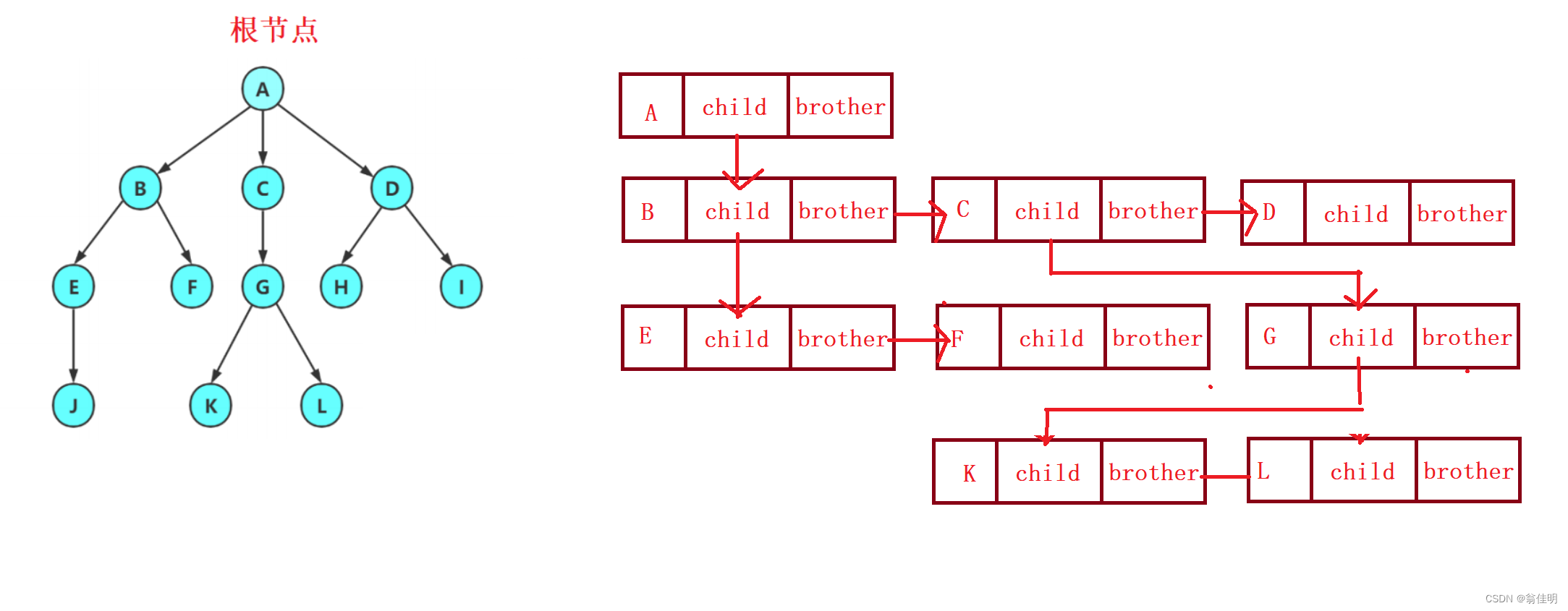
class Node{

    int val;//存储的数据
    Node firstChild;//第一个孩子引用
    Node nextBrother;//下一个兄弟引用
}

一个结点中，val存储数据
firstChild存该结点的第一个子结点
nextBrother存该结点下一个兄弟结点
没有孩子兄弟的时候为null

孩子双亲表示法

2.树的应用

文件夹结构

二、二叉树

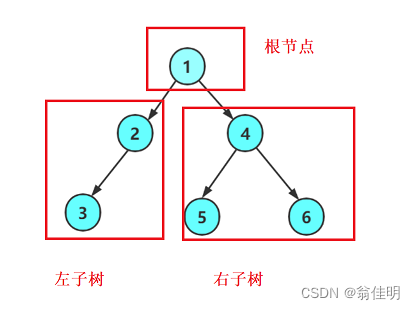
1.二叉数的概念

• 一个根节点加上它的左子树和右子树
• 二叉树不存在度大于2的结点（一个结点只能有两个子节点）
• 二叉树是有序树，子树的左右不能颠倒

2.满二叉树

1.每一层的结点都是满的，除了最后一层，每个结点都有两个子结点
2.每层的结点数都达到最大值
3.如果二叉树的层数为K,结点总数为2^k-1,则为满二叉树
4.结点为n,层数 = log2(n+1),向上取整

3.完全二叉树

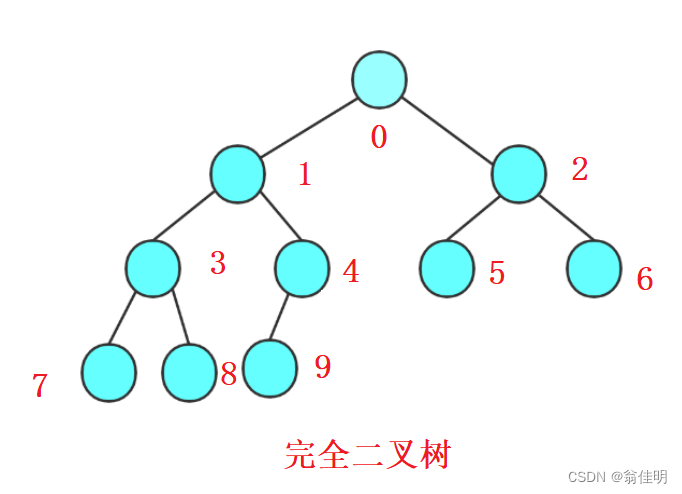
1.从0开始依次从左往右按顺序一一对应
2.满二叉树是一种特殊的完全二叉树

4.二叉树的性质

• 1.根结点的层数为1，则一棵非空二叉树的第i层上最多有 2^(i-1) 个结点
• 2.根结点的二叉树的深度为1，深度为K的二叉树的最大结点数是 2^K-1
• 3.具有n个结点的完全二叉树的深度k==log2(n+1) ,向上取整
• 4.对于具有n个结点的完全二叉树，如果按照从上至下从左至右的顺序对所有节点从0开始编号，则对于序号为i的结点有：

父结点下标为 i : 左孩子的下标：2i+1 ; 右孩子的下标 2i+2;
子结点下标为 i : 父结点下标：（i - 1）/ 2

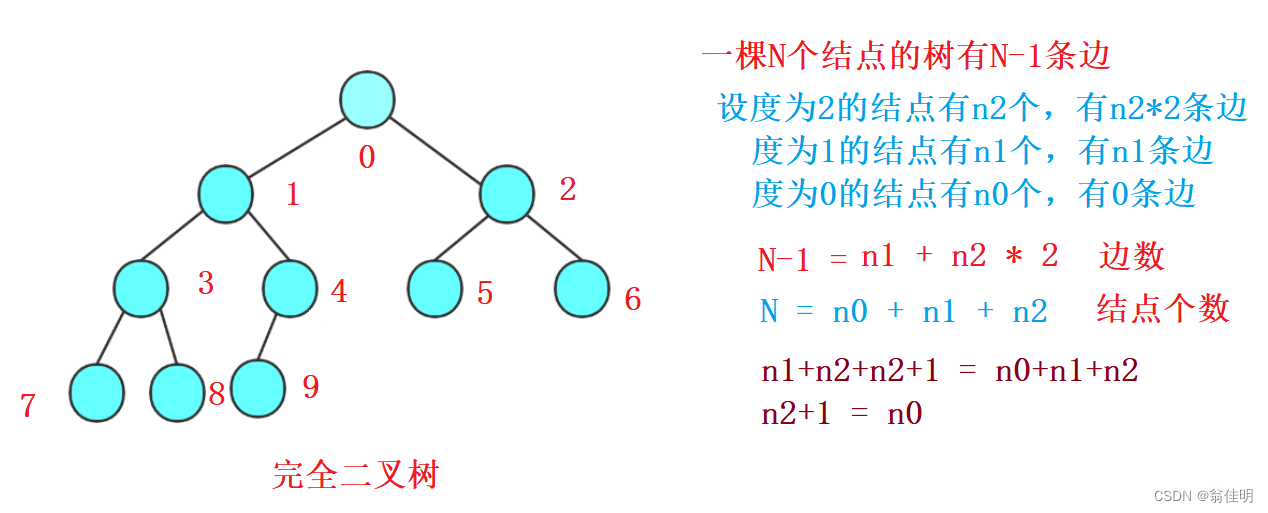
• 5.对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0＝n2＋1

也就是说：度为0的结点比度为2的结点多一个==有两个子节点的结点数=叶子结点数-1
n0＝n2＋1

练习：

A.n
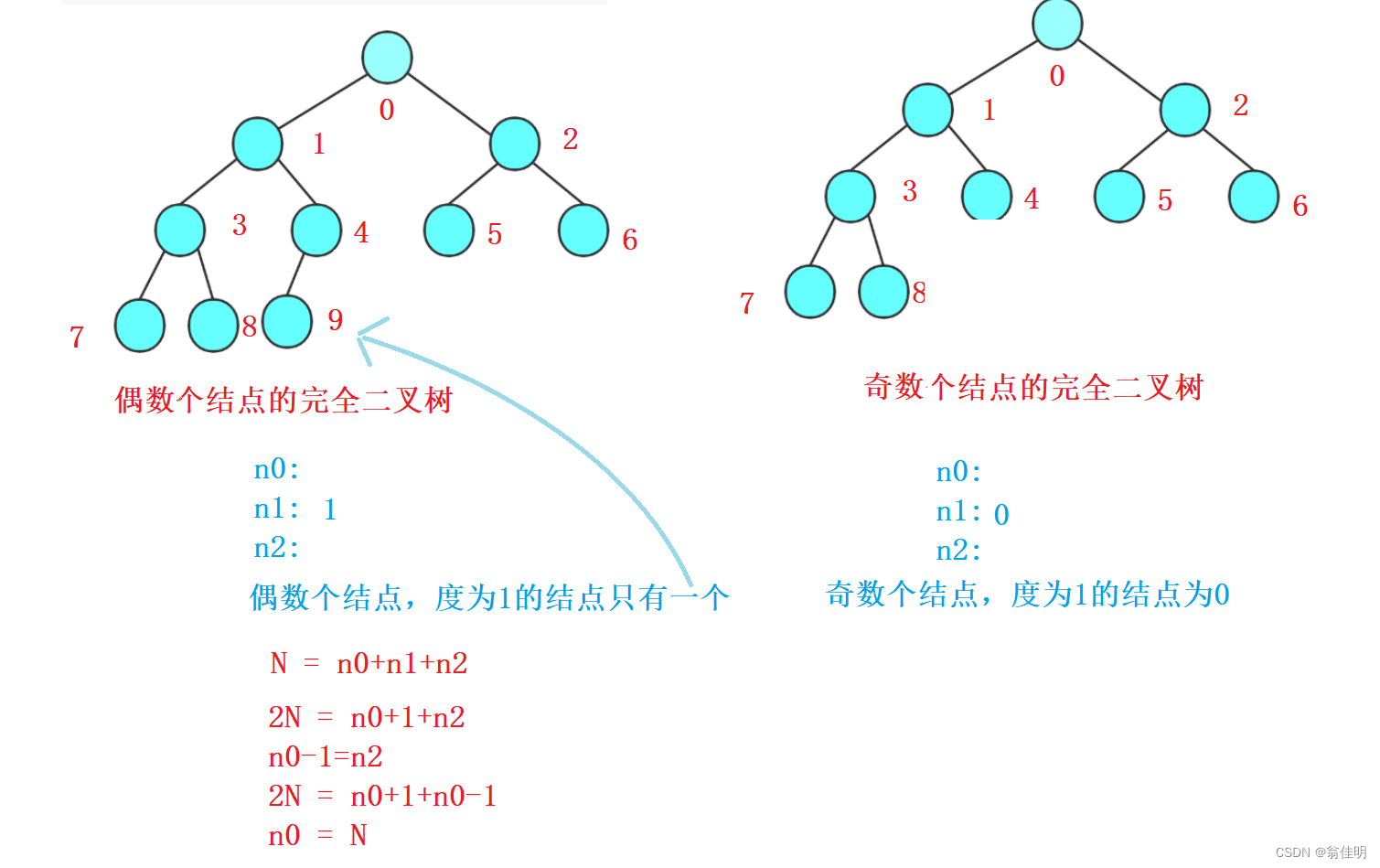
完全二叉树结点的个数分奇数和偶数两种情况
奇数个结点，度为1的结点数为1
偶数个结点，度为1的结点数为0
联立总结点数之和的式子和 n0-1=n2

点击移步博客主页，欢迎光临~