队列的表示和实现

相关术语

• 队列（Queue）是仅在表尾进行插入操作，在表头进行删除操作的线性表。
• 表尾即an端，称为队尾；表头即在a1端，称为对头。
• 是一种先进先出的线性表。
  
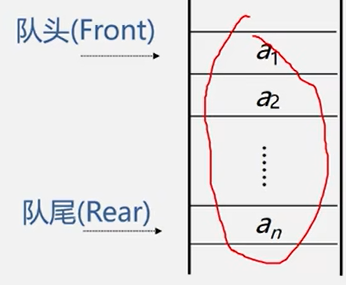
  插入元素称为入队，删除元素称为出队。
  队列的存储结构为链队或顺序对（常用循环顺序对）。

队列的表示

队列的顺序表示-----用一维数组base[MAXQSIZE]。

//定义队列
typedef struct {
	int* base;//初始化的动态分配内存空间
	int front;//头指针
	int rear;//尾指针
}SqQueue;
}

初始：front = rear = 0;

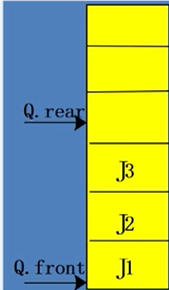
J1,J2,J3入队
入队：base[rear] = x;
rear++;

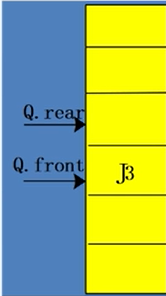
J1,J2出队
出队：x = base[front];
front++;
空对标志：front = rear;

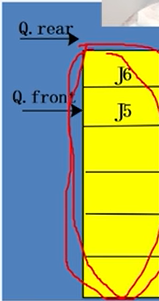
这里的J6已经满了，J3,J4还能入队吗？
当rear=MAXQSIZE时，发生溢出。

1. 当front = 0;
   rar = MAXQSIZE时再出队真溢出.
   

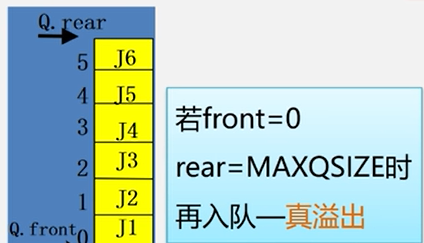
2. 当front！=0；rear = MAXQSIZE时，再入队，假溢出。
   
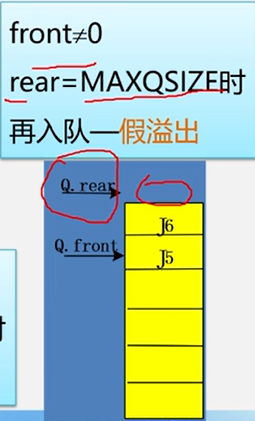
   解决上溢的方法----引入循环队列
   base[0]接在base[MAXQSIZE-1]之后，若rear+1 == M，则令rear= 0；
   实现方法：利用模运算（mod）。
   插入元素：Q.base[Q.rear] = x;
   Q.rear = (Q.rear+1) % MAXQSIZE;
   删除元素：x = Q.base[s.front]
   Q.front = (Q.front+1) % MAXQSIZE;
   
   这里引发了一个二义性，就是front= rear为空队列。需要进行讨论。
   循环队列解决对满时的判断方法----少用一个元素空间。
   
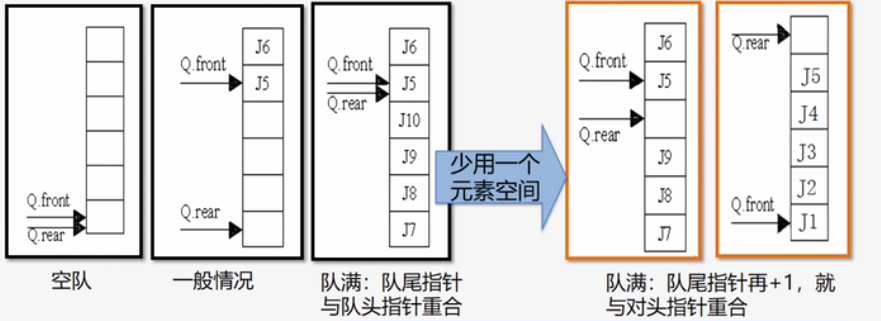
   队空：front == rear;

队满：（rear+1）%MAXQSIZE == front；

链队的表示

若用户无法估计所用队列的长度，则宜采用链队列。

链队的定义

//链队列的类型队列
typedef struct Qnode {
	int data;
	struct Qnode* next;
}QNode,*QueuePtr;
typedef struct {
	QueuePtr front;//队头指针
	QueuePtr rear;//对尾指针
}LinkQueue;

链队的初始化

//初始化
void InitQueue(LinkQueue Q) {
	Q.front = Q.rear = new QNode;//生成新结点作为头结点，队头和队尾指针指向此结点
	Q.front->next = NULL;//将空结点的next域置空
}

销毁链队列

void DestroyQueue(LinkQueue Q) {
	while (Q.front)
	{
		QueuePtr p;
		p = Q.front->next;
		free(Q.front);
		Q.front = p;
	}
}

链队列的入队

//将元素e入队
void EnQueue(LinkQueue Q, int e) {
	QueuePtr q = new QNode;
	if (!q) {
		exit(0);
		q->data = e;
		q->next = NULL;
		Q.rear->next = p;
		Q.rear = p;
	}
}

出栈

int DeQueue(LinkQueue Q, int e) {
	if (Q.front == Q.rear) {
		return 0;
	}
	QueuePtr p = Q.front->next;
	e = p->data;
	Q.front->next = p->next;
	delete p;
	return 1;
}