文章目录
- 1、并查集
- 2、了解图
- 3、邻接矩阵
- 4、压缩路径
- 5、基本概念
- 6、邻接表
1、并查集
并查集是一个森林,是由多棵树组成的。这相当于整套数据,分成多个集合。查找有交集的集合们,会把它们合并起来,所以叫并查集。
一开始拿到的是一堆数据,我们给它们编号,然后放到一个个集合中。如何做编号?如何做集合?我们先建立两个文件,Graph.cpp和UnionFindSet.h。
#include <iostream>
using namespace std;
int main()
{
string a[] = { "张三", "李四", "王五", "赵六" };
UnionFindSet<string> ufs(a, 4);
return 0;
}
#pragma once
#include <vector>
#include <map>
template <class T>
class UnionFindSet
{
public:
UnionFindSet(const T* a, size_t n)
{
}
private:
vector<T> _a;
};
把接收到的a保存到_a,这样每个人编号就是下标了,但这不是好办法。
class UnionFindSet
{
public:
UnionFindSet(const T* a, size_t n)//建立映射关系
{
for (size_t i = 0; i < n; ++i)
{
_a.push_back(a[i]);
_indexMap[a[i]] = i;
}
}
private:
vector<T> _a;//下标就是编号,编号找人
map<T, int> _indexMap//但通过人找编号更合理,这样不需要每次都得遍历才能找到一个人
};
通过这样的代码可以简单理解一下编号是怎么回事,但代码不是这样写的。接下来看看集合。集合本质就是树,选择一个根节点,然后几个编号作为它的子节点,但该选哪几个编号作为一个树呢?这里的用的树是双亲表示法,每个孩子都存储它的双亲节点。还是用数组来表示,最一开始都初始化为-1,意思就是每个编号单独成一个集合

构成集合后会是这样
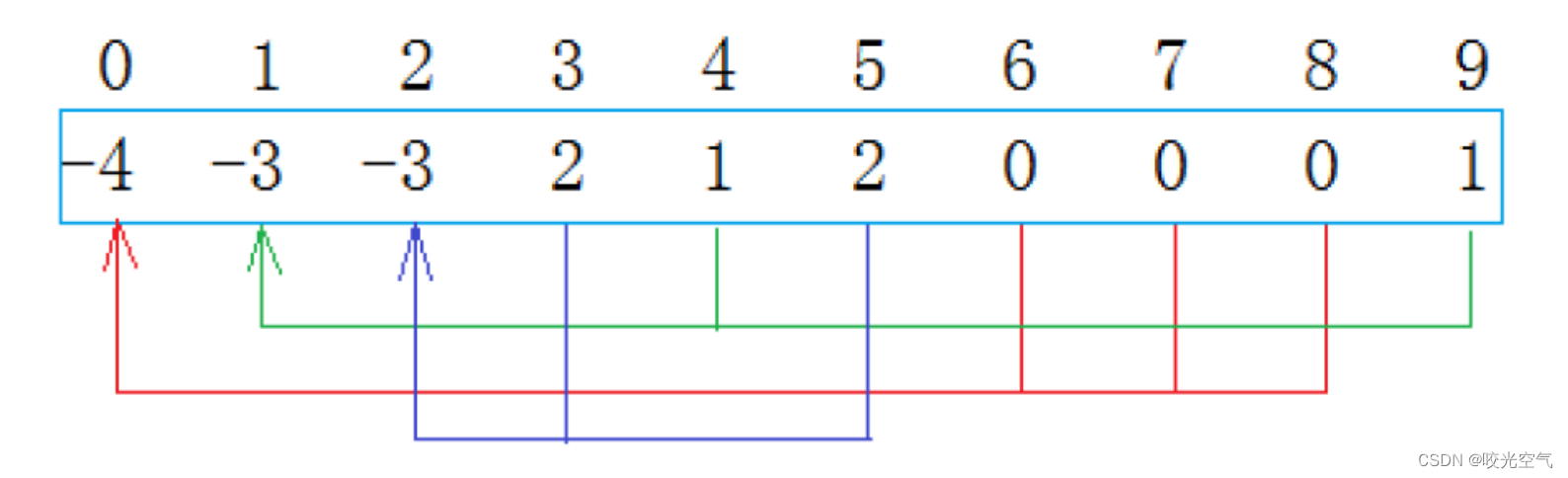
0和678作为一棵树,0作为根,6是孩子节点,把6的-1加过去,0位置变成-2,6位置存上双亲节点0,然后是7和8。这样的规则下,数组的下标就是集合中元素的编号,比如arr[0],就是编号为0的数据;每个位置存储的数字,如果为负数,说明当前编号是根,数字的绝对值就是这棵树的节点数量;如果数字为非负数,那么当前位置存储的就是这个编号的双亲编号。比如arr[6] = 0,6这个编号的双亲编号就是0,arr[0] = -4,0编号是根,节点数量是4。
假设4和8建立了联系,这两个集合要合并。这里要如何合并?根节点是谁?根节点是谁都可以,既可以是0也可以是1,选一个就好。假如选0做根节点,那么0就要加上1位置的数,1的位置存储0,4和9不变。

下面是完善后的并查集类
#pragma once
#include <vector>
#include <iostream>
using namespace std;
class UnionFindSet
{
public:
UnionFindSet(size_t n)//给编号数量
:_ufs(n, -1)
{}
void Union(int x1, int x2)//给两个编号,合并
{
//得先判断这两个编号能不能合并
int root1 = FindRoot(x1);
int root2 = FindRoot(x2);
//本身在一个集合,就不需要合并
if (root1 == root2) return;
//可以合并的话就自己做规定怎么合并,这里就让小的编号做根
if (root1 > root2) swap(root1, root2);
_ufs[root1] += _ufs[root2];
_ufs[root2] = root1;
}
int FindRoot(int x)//找一个编号的根
{
int parent = x;
while (_ufs[parent] >= 0)//此时说明它本身不是根,就看存的值,往上找父节点,因为父节点可能不是根,所以需要while
{
parent = _ufs[parent];//对照上面的图来看
}
return parent;//小于0说明自己就是根,直接返回
}
bool InSameSet(int x1, int x2)//看看编号在不在一个集合里
{
return FindRoot(x1) == FindRoot(x2);
}
size_t SetSize()
{
size_t size = 0;
for (size_t i = 0; i < _ufs.size(); i++)
{
if (_ufs[i] < 0) ++size;
}
return size;
}
private:
vector<int> _ufs;
};
看一道题,剑指offer的。
LCR 116. 省份数量
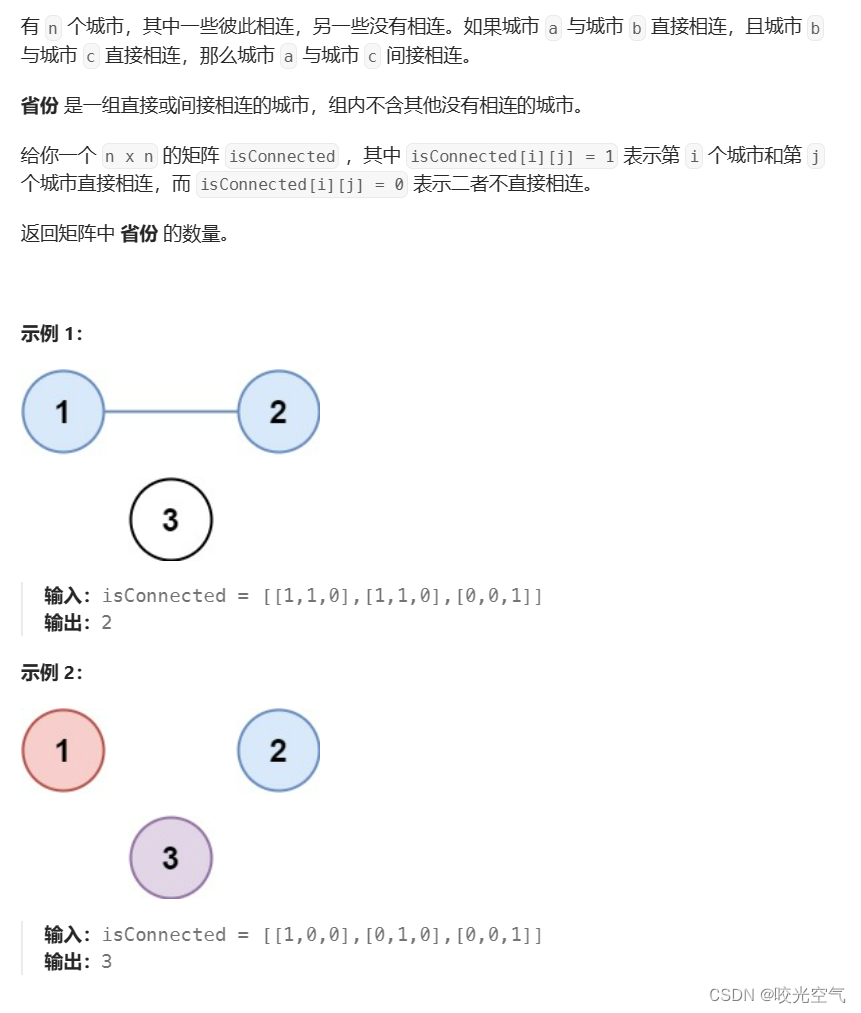
把我们写好的并查集类拿过来使用
class UnionFindSet
{
public:
UnionFindSet(size_t n)
:_ufs(n, -1)
{}
void Union(int x1, int x2)
{
int root1 = FindRoot(x1);
int root2 = FindRoot(x2);
if (root1 == root2) return;
if (root1 > root2) swap(root1, root2);
_ufs[root1] += _ufs[root2];
_ufs[root2] = root1;
}
int FindRoot(int x)
{
int parent = x;
while (_ufs[parent] >= 0)
{
parent = _ufs[parent];
}
return parent;
}
bool InSameSet(int x1, int x2)
{
return FindRoot(x1) == FindRoot(x2);
}
size_t SetSize()
{
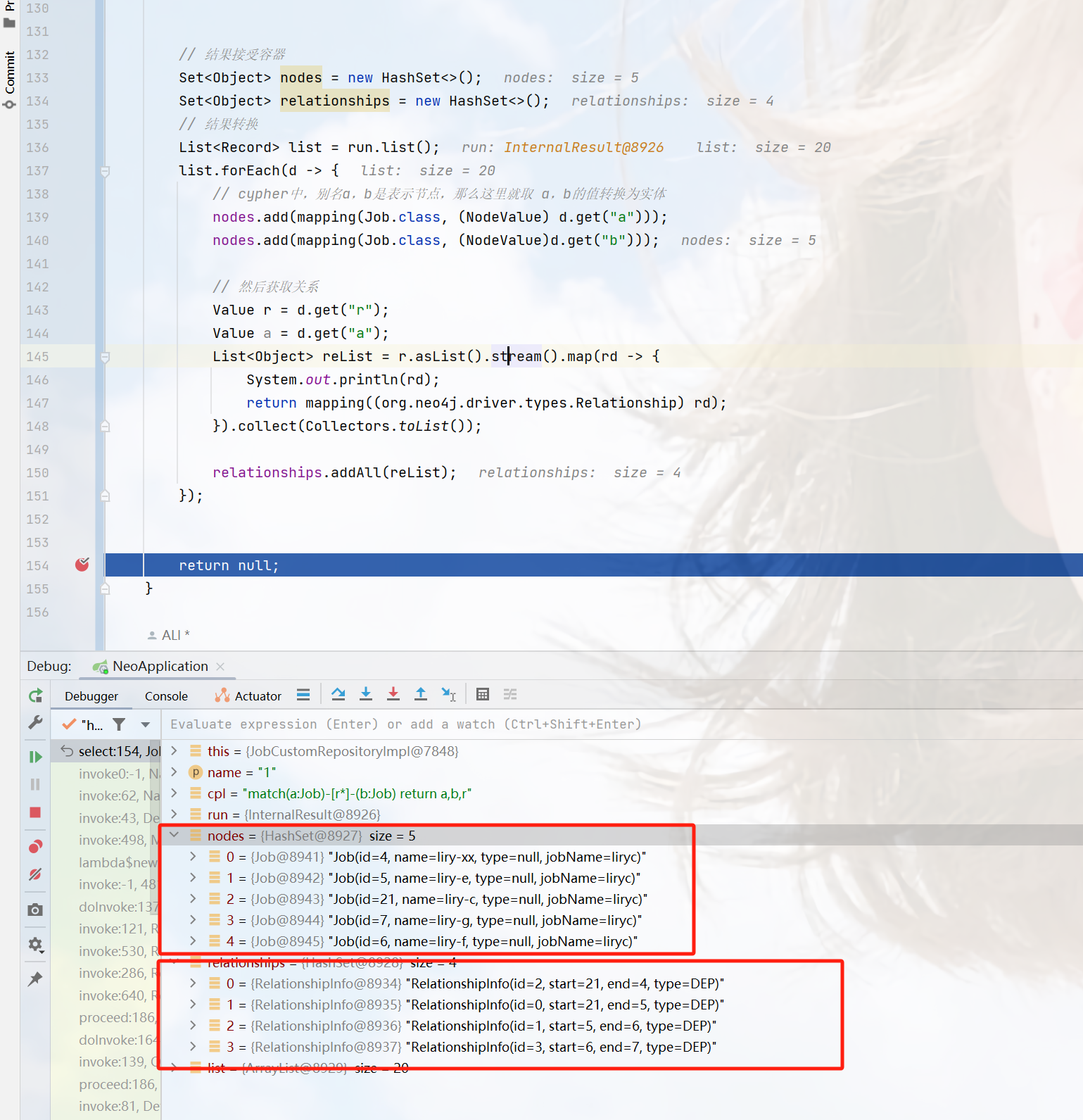
size_t size = 0;
for (size_t i = 0; i < _ufs.size(); i++)
{
if (_ufs[i] < 0) ++size;
}
return size;
}
private:
vector<int> _ufs;
};
class Solution {
public:
int findCircleNum(vector<vector<int>>& isConnected) {
UnionFindSet ufs(isConnected.size());
for(size_t i = 0; i < isConnected.size(); ++i)
{
for(size_t j = 0; j < isConnected[i].size(); ++j)
{
if(isConnected[i][j] == 1)//是1说明两个城市相连,那就可以进入一个集合,所以用Union
ufs.Union(i, j);
}
}
return ufs.SetSize();
}
};
如果不用并查集,应该怎么写?那就现场写几个用到的函数
int findCircleNum(vector<vector<int>>& isConnected) {
vector<int> ufs(isConnected.size(), -1);
auto findRoot = [&ufs](int x)
{
while(ufs[x] >= 0)
x = ufs[x];
return x;
};
for(size_t i = 0; i < isConnected.size(); ++i)
{
for(size_t j = 0; j < isConnected[i].size(); ++j)
{
if(isConnected[i][j] == 1)
{
//合并集合
int root1 = findRoot(i);
int root2 = findRoot(j);
if(root1 != root2)
{
ufs[root1] += ufs[root2];
ufs[root2] = root1;
}
}
}
}
int count = 0;
for(auto e : ufs)
{
if(e < 0) ++count;
}
return count;
}
压缩路径:
当数据量比较大时会出现一棵树下来连接了很多层子树,这时候如果每次都要一点点往上找根,效率就比较低。这时候就要用压缩路径,压缩路径在findRoot函数中使用。查找一次比较深的节点的根后,我们发现需要减少一下层数,这个可以用一个变量来记录循环次数,当大于某个数时就得做压缩了。假设查找的是x节点的根,查找完后,就把x节点位置存储的值变成根节点的编号,这样就是把这个节点直接调为根节点的孩子,并且把x节点原父节点也调成根节点的孩子,但x节点的原兄弟节点不动。如果从根到x有3层,调整完后就变成了2层,等到再查找x节点原兄弟节点时,再把这个兄弟节点调成根的孩子,而这个兄弟节点的父节点就还是根的孩子。通过不断地调整,要做到的结果就是原本3层,变成1层,都变成根的孩子节点,这些节点的父节点都是根。
练题时,如果超时,估计就要用压缩路径了。
另一个题
990. 等式方程的可满足性

我们可以先遍历一遍,为等号的都放到一个集合里,再去看不相等的符号的,如果不相等的两个在一个集合里,那就false,不是那就继续。
bool equationsPossible(vector<string>& equations) {
vector<int> ufs(26, -1);
auto findRoot = [&ufs](int x)
{
while(ufs[x] >= 0)
x = ufs[x];
return x;
};
//第一次遍历,把相等的值放到一个集合中
for(auto& str : equations)
{
if(str[1] == '=')
{
int root1 = findRoot(str[0] - 'a');
int root2 = findRoot(str[3] - 'a');
if(root1 != root2)
{
ufs[root1] += ufs[root2];
ufs[root2] = root1;
}
}
}
//第二遍,判断不相等的在不在一个集合,在就false
for(auto& str : equations)
{
if(str[1] == '!')
{
int root1 = findRoot(str[0] - 'a');
int root2 = findRoot(str[3] - 'a');
if(root1 == root2) return false;
}
}
return true;
}
2、了解图
图是一种数据结构,图由顶点集合和边的集合构成,通常都会用G(V, E)来表示,V就是顶点集合,E就是边集合,所以G(V, E)的意思就是图由顶点(集合)和边(集合)组成。常见的图

树是一种特殊的图,无环,连通。树关注节点(顶点)中存的值,图关注的是顶点和边的权值。边如何表示?边连接两个点,还有权值,所以它是一个二维数组,e[i][j]就表示顶点i和j之间的边,这个位置的值就是权值。图分为有向图和无向图,也就是有方向箭头和没有方向箭头,无向图的两个顶点可以互相连接,有向图只能按照既定方向去走。
边的含义可以有很多,它不止是表示距离,也可以表示两个城市(顶点)之前坐高铁的时间,两个顶点的关系等。针对图有一些种类的问题,深度/广度优先,最小生成树,最短路径等,这些后面再写。
微信,qq是经典的无向图,无向图通常用来表示强社交关系,微博,bzhan等就是有向图,是一种弱社交关系,媒体社交。qq中有亲密度,亲密度就是权值。短视频的推荐算法也和图有关。
图有两个结构,邻接矩阵和邻接表。邻接矩阵存边的集合。每个顶点先假设下标,比如ABCD就是0123,这样一个二维数组的邻接矩阵,每个位置的值就表示权值,[i][j],ij相等,那就存0,表示是同一顶点,ij不同,如果之间没有关系,那就填上无穷这样的数字,也可以填别的,有向图可能可以从2到3,但不能从3到2,那么[3][2]就会是无穷。如果权值表示两个点之间的关系,那么就填为1或0。当然,规则由自己决定。
邻接矩阵存储方式非常适合稠密图,因为无论稠密还是稀疏,邻接矩阵都是每个位置都有值;邻接矩阵可以判断两个顶点的连接关系,并取到权值。但相对而言,邻接矩阵不适合查找一个顶点连接的所有边,它需要O(N),比如找顶点4连接的点,它就得遍历一下,每个边都得看一下那个位置的值。
邻接表
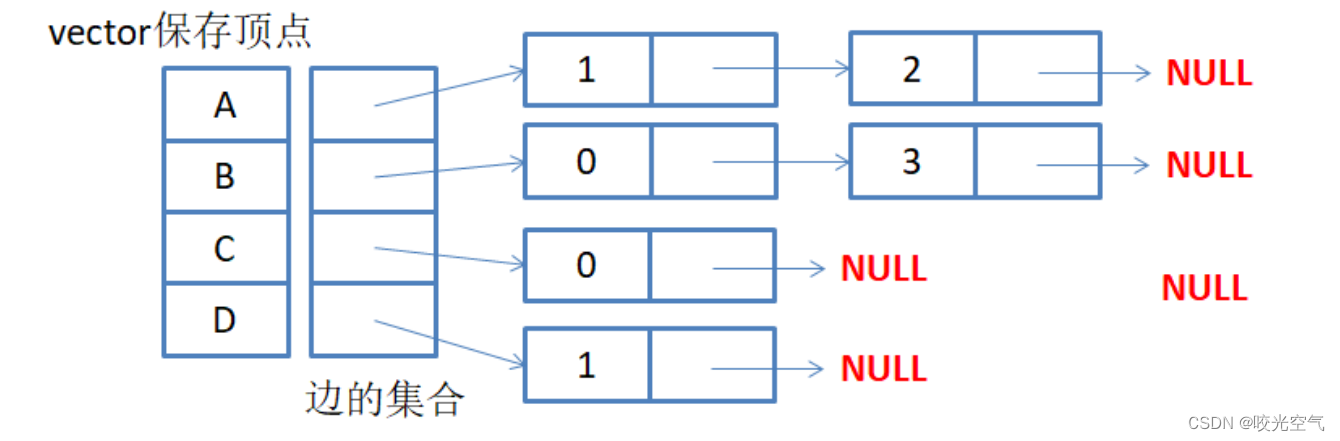
它是一个指针数组,把自己连接的所有点都挂在下面。它也能表示有无向。
邻接表适合存储稀疏图,适合查找一个顶点连接出去的边,因为只需要遍历连接的顶点的数,但不适合确定两个顶点是否相连和权值。
有向图情况下,会有入边表和出边表,就是A挂着的顶点B,入边表意思就是从B到A,出边表意思就是从A到B。一般只需要一个出边表即可。
邻接矩阵和邻接表是相辅相成,各有缺点的互补结构。
3、邻接矩阵
我们创建Graph.h文件,先写一个框架
#pragma once
#include <vector>
#include <map>
#include <iostream>
using namespace std;
namespace matrix
{
template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>//W权值,Direction表示有无向,false表示无向
//中间加的MAX_W,其实就是非类型模版参数,是用来初始化邻接矩阵的,也可以传其它值
class Graph
{
public:
Graph(const V* a, size_t n)//创造图,手动添加
{
_vertexs.reserver(n);
for (size_t i = 0; i < n; ++i)
{
_vertexs.push_back(a[i]);
_indexMap[a[i]] = i;
}
_matrix.resize(n);
for (size_t i = 0; i < _matrix.size(); ++i)
{
_matrix[i].resize(n, MAX_W);
}
}
size_t GetVertexIndex(const V& v)//确定顶点下标,虽然都在map里,但还是要有一个函数
{
}
void AddEdge(const V& src, const V& dst, const W& w)//增加边的话,应当传源点,目标点,权值
{
}
private:
vector<V> _vertexs;//顶点集合,比如ABCD
//有稀疏图,稠密图的叫法,就是在说边的多少
map<V, int> _indexMap;//顶点映射下标,比如ABCD变为1234
vector<vector<W>> _matrix;//邻接矩阵,展示顶点之间的关系和权值
};
};
Graph构造函数那里就创建了一个图,三个成员都被初始化完成,传进来的就是一个数组a和顶点个数。接下来要开始添加边,在这之前先确定好顶点下标。
讲解在代码中
size_t GetVertexIndex(const V& v)//确定顶点下标,虽然都在map里,但还是要有一个函数
{
auto it = _indexMap.find(v);
if ( it != _indexMap.end())
{
return it->second;
}
else
{
throw invalid_argument("顶点不存在");//非法参数异常
return -1;//抛异常是运行逻辑,程序走到这里会抛,但编译器不管运行逻辑,还是要检查这个函数是否正确结束,所以要返回。
}
}
void AddEdge(const V& src, const V& dst, const W& w)//增加边的话,应当传源点,目标点,权值
{
//即使抛异常程序还能执行,但程序员已经知道程序错误了,最后程序正常地异常结束
//assert则是暴力退出,且只在debug模式下才有assert,release模式下就屏蔽assert了
size_t srci = GetVertexIndex(src);
size_t dsti = GetVertexIndex(dst);
//有向图和无向图区分
_matrix[srci][dsti] = w;
if (Direction == false)
_matrix[dsti][srci] = w;
}
打印函数
void Print()
{
size_t n = _vertexs.size();
//顶点
for (size_t i = 0; i < n; ++i)
{
cout << "[" << i << "]" << "->" << _vertexs[i] << endl;
}
cout << endl;
//打印横下标
cout << " ";
for (size_t i = 0; i < n; ++i)
{
cout << i << " ";
}
cout << endl;
for (size_t i = 0; i < _matrix.size(); ++i)
{
cout << i << " ";//打印竖下标
for (size_t j = 0; j < _matrix[i].size(); ++j)
{
if (_matrix[i][j] == MAX_W)
{
cout << "* ";
}
else cout << _matrix[i][j] << " ";
}
cout << endl;
}
cout << endl;
}
测试代码
void TestGraph1()//放在matrix命名空间里
{
Graph<char, int, INT_MAX, true> g("0123", 4);
g.AddEdge('0', '1', 1);
g.AddEdge('0', '3', 4);
g.AddEdge('1', '3', 2);
g.AddEdge('1', '2', 9);
g.AddEdge('2', '3', 8);
g.AddEdge('2', '1', 5);
g.AddEdge('2', '0', 3);
g.AddEdge('3', '2', 6);
g.Print();
}
int main()
{
matrix::TestGraph1();
return 0;
}
到现在为止,代码没有问题,我们来改进一下功能实现。
合并集合的时候,是让数量小的集合合并到大的,还是大的合并到小的,这里小的合并到大的为好。默认root1为数量大的
if (abs(_ufs[root1]) < abs(_ufs[root2])) swap(root1, root2);
_ufs[root1] += _ufs[root2];
_ufs[root2] = root1;
4、压缩路径
不用递归写,毕竟是在压缩深度深的树。用非递归写。
int FindRoot(int x)//找一个编号的根
{
int root = x;
while (_ufs[root] >= 0)//此时说明它本身不是根,就看存的值,往上找父节点,因为父节点可能不是根,所以需要while
{
root = _ufs[root];//对照上面的图来看
}
//压缩路径
while (_ufs[x] >= 0)
{
int parent = _ufs[x];
_ufs[x] = root;
x = parent;
}
return root;//小于0说明自己就是根,直接返回
}
这里就是一次把当前节点到根节点之间的所有节点都变成根的孩子。
5、基本概念
完全图是最稠密的图,任意两个顶点之间都直接相连 。在有n个顶点的无向图中,若有n × (n-1)/2条边,即任意两个顶点之间有且仅有一条边,
则称此图为无向完全图;在n个顶点的有向图中,若有n × (n-1)条边,即任意两个顶点之间有且仅有方向相反的边,则称此图为有向完全图。
邻接顶点。就是两个顶点之间有边,就是两个邻接顶点。在无向图中G中,若(u, v)是E(G)中的一条边,则称u和v互为邻接顶点,并且称边(u,v)依附于顶点u和v;在有向图G中,若<u, v>是E(G)中的一条边,则称顶点u邻接到v,顶点v邻接自顶点u,并且称边<u, v>与顶点u和顶点v相关联。
顶点的度指的是与这个顶点相连的边的数量,记作deg(v)。有向图有入度和出度,也就是1这个顶点,1到3有1条边,2到1有2条边,所以1的入度是2,出度是1。
路径则好理解,从一个顶点到另一个顶点都可以走哪些边,这些边就组成了路径。路径可以有很多条,也就出现了最短路径问题。
路径长度。对于不带权的图,一条路径的路径长度是指该路径上的边的条数;对于带权的图,一条路径的路径长度是指该路径上各个边权值的总和。
简单路径与回路。若路径上各顶点v1,v2,v3,…,vm均不重复,则称这样的路径为简单路径。若路径上第一个顶点v1和最后一个顶点vm重合,则称这样的路径为回路或环。
子图。子图的顶点和边都是原图的一部分。
连通图。在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的,则称此图为连通图。
强连通图:在有向图中,若在每一对顶点vi和vj之间都存在一条从vi到vj的路径,也存在一条从vj到vi的路径,则称此图是强连通图。
任意点之间都有路径到达,无向图中叫连通图,有向图中叫强连通图。
生成树:一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n-1条边。注意这是无向图中的概念。
6、邻接表
邻接表要用到哈希。用上面邻接矩阵的代码做一下改动。
template <class W>
struct Edge
{
int _dsti;//目标点的下标
W _w;
};
template<class V, class W, bool Direction = false>//这里就不需要INT_MAX了
class Graph
{
typedef Edge<W> Edge;
public:
Graph(const V* a, size_t n)
{
_vertexs.reserve(n);
for (size_t i = 0; i < n; ++i)
{
_vertexs.push_back(a[i]);
_indexMap[a[i]] = i;
}
}
size_t GetVertexIndex(const V& v)
{
auto it = _indexMap.find(v);
if (it != _indexMap.end())
{
return it->second;
}
else
{
throw invalid_argument("顶点不存在");
return -1;
}
}
void AddEdge(const V& src, const V& dst, const W& w)
{
size_t srci = GetVertexIndex(src);
size_t dsti = GetVertexIndex(dst);
}
void Print()
{
size_t n = _vertexs.size();
for (size_t i = 0; i < n; ++i)
{
cout << "[" << i << "]" << "->" << _vertexs[i] << endl;
}
cout << endl;
}
private:
vector<V> _vertexs;//顶点集合
map<V, int> _indexMap;//顶点映射下标
vector<Edge*> _tables;//邻接表
};
然后完善,在命名空间里添加一个结构体,类里再使用它
template <class W>
struct Edge
{
size_t _dsti;//目标点的下标
W _w;
Edge<W>* _next;
Edge(size_t dsti, const W& w)
:_dsti(dsti)
, _w(w)
, _next(nullptr)
{}
};
template<class V, class W, bool Direction = false>//这里就不需要INT_MAX了
class Graph
{
typedef Edge<W> Edge;
public:
Graph(const V* a, size_t n)
{
_vertexs.reserve(n);
for (size_t i = 0; i < n; ++i)
{
_vertexs.push_back(a[i]);
_indexMap[a[i]] = i;
}
_tables.resize(n, nullptr);
}
void AddEdge(const V& src, const V& dst, const W& w)
{
size_t srci = GetVertexIndex(src);
size_t dsti = GetVertexIndex(dst);
Edge* eg = new Edge(dsti, w);
//采用头插,尾插需要找尾,不如头插更有效率
eg->_next = _tables[srci];
_tables[srci] = eg;
if (Direction == false)//如果是无向图
{
Edge* eg = new Edge(srci, w);
eg->_next = _tables[dsti];
_tables[dsti] = eg;
}
}
void Print()
{
size_t n = _vertexs.size();
for (size_t i = 0; i < n; ++i)
{
cout << "[" << i << "]" << "->" << _vertexs[i] << endl;
}
cout << endl;
for (size_t i = 0; i < n; ++i)
{
cout << endl;
cout << _vertexs[i] << "[" << i << "]";
Edge* cur = _tables[i];
while (cur)
{
printf(" - %-3d -> ", cur->_w);
cout << _vertexs[cur->_dsti] << "[" << cur->_dsti << "]";
cur = cur->_next;
}
cout << " -> nullptr" << endl;
}
}
测试
void TestGraph2()
{
string a[] = { "张三", "李四", "王五", "赵六" };
Graph<string, int> g1(a, 4);
g1.AddEdge("张三", "李四", 100);
g1.AddEdge("张三", "王五", 200);
g1.AddEdge("王五", "赵六", 30);
g1.Print();
}
本篇gitee
下一篇开始写图的算法。
结束。