Pumarola A, Corona E, Pons-Moll G, et al. D-nerf: Neural radiance fields for dynamic scenes[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2021: 10318-10327.
D-Nerf 较 NeRF 的改进 1 就是能够建模移动或变形的物体,包括铰接运动以及人类的复杂姿势。通过在输入中增加时间变量 t t t,可以预测某空间点在该时刻的位移,再结合 NeRF 的标准网络就能够建模动态场景。
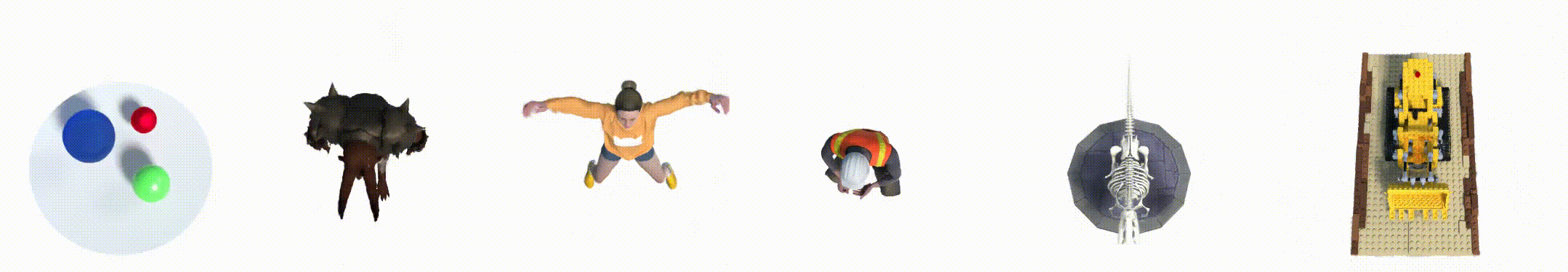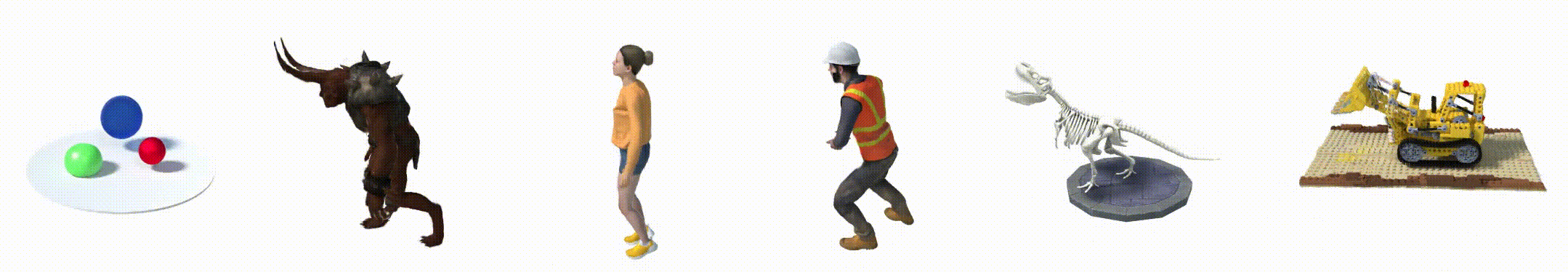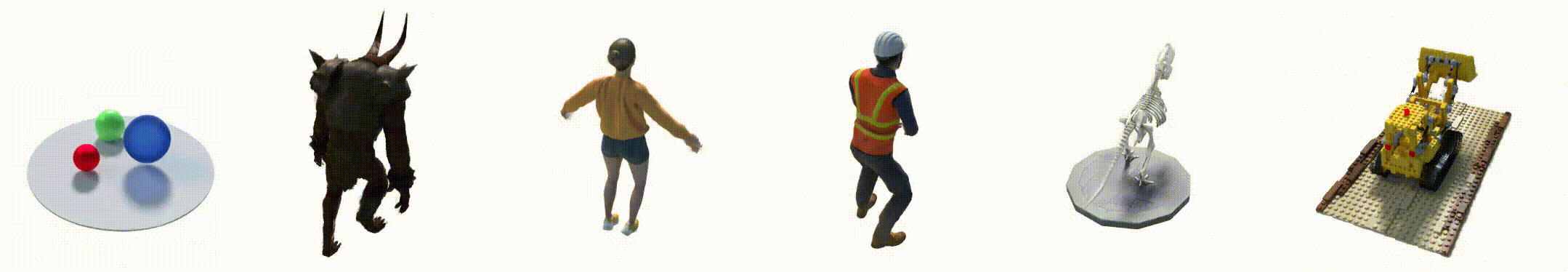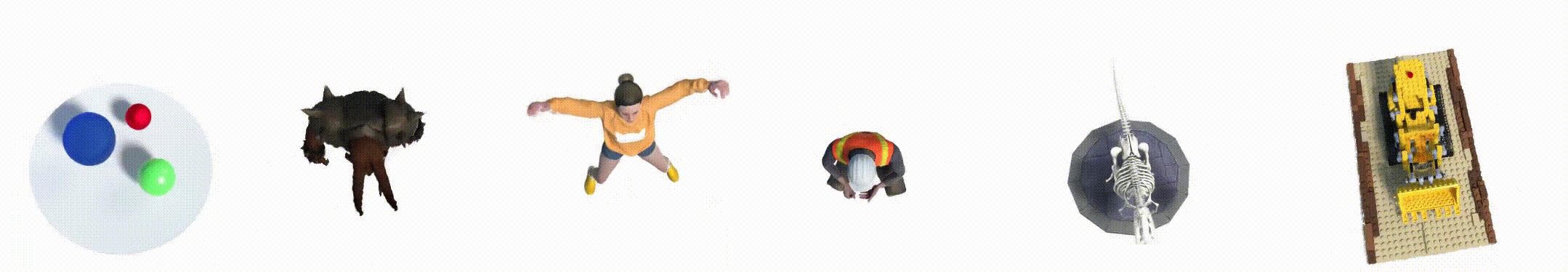
目录
- 一. 研究思路
- 1. 场景表示
- 2. 新视图渲染
- 二. 动态神经辐射场
- 1. 标准网络
- 2. 变形网络
- 三. 新视图渲染
- 四. 实验结果
- 1. 实验细节
- 2. 数据集
- 3. 实验效果
- 4. 对比实验
- 5. 副产品
- 五. 总结
- 六. 复现
一. 研究思路
- 神经渲染 (neural rendering) 用于视图合成已经取得了重大成果,以 NeRF 及其变体为代表尤为突出。
- 但目前的 NeRF 方法都是基于静态场景的假设,无法建模移动或变形的物体。
- 文章放宽了 NeRF 的静态场景假设,提出了一种端到端的 NeRF 变体,用于建模静态、移动或变形物体组成的动态场景,称为 D-Nerf。
端到端 (end-to-end):直接从输入数据到最终输出进行训练,而不需要手动设计中间步骤、设计特征提取或者增加额外组件。
和现有的 4D 视图合成技术不同,D-Nerf 只需要一台摄像机,不需要显式的三维重建,并且还可以进行端到端的训练。
文中全面评估了 D-NeRF 在各种场景下的表现,从铰接运动到人类的复杂姿势。通过将场景学习分解为标准场景和场景流以及控制时间变量,D-NeRF 能够渲染高质量的图像。
D-NeRF 还有一个副产品,就是能够产生完整的三维网格,捕捉时变几何。
1. 场景表示
在 NeRF 的场景表示函数的五维输入 ( x , y , z , θ , ϕ ) (x, y, z, θ, ϕ) (x,y,z,θ,ϕ) 的基础上,增加时间变量 t t t。但仅仅使用 ( x , y , z , θ , ϕ , t ) → ( c , σ ) (x, y, z, θ, ϕ, t) \rightarrow (\bold{c}, σ) (x,y,z,θ,ϕ,t)→(c,σ) 并不能得到满意的结果,因为没有充分利用时间冗余信息。
时间冗余 (temporal redundancy):当处理连续时间中的动态场景时,通常会有许多相似的或几乎相同的场景信息在相邻的时间步骤中出现。这种情况下,将每个时间步骤都视为独立的输入会导致低效的学习和生成结果。
因此将场景的学习过程分为两个模块:
- 空间映射: ( x , y , z , t ) → ( Δ x , Δ y , Δ z ) (x, y, z, t) \rightarrow (\Delta x, \Delta y, \Delta z) (x,y,z,t)→(Δx,Δy,Δz),即变形场;
- 回归预测: ( x + Δ x , y + Δ y , z + Δ z , θ , ϕ ) → ( c , σ ) (x+\Delta x, y+\Delta y, z+\Delta z, θ, ϕ) \rightarrow (\bold c, \sigma) (x+Δx,y+Δy,z+Δz,θ,ϕ)→(c,σ),即原始 NeRF;
这两个模块都使用没有卷积层的深度全连接网络(即多层感知机)来学习得到。
2. 新视图渲染
学习得到 D-Nerf 的场景表示后,可以使用
(
θ
,
φ
,
t
)
(θ, φ, t)
(θ,φ,t) 控制新视图的渲染了。

文中还提出以下假设:
- 场景中的每个点可以变换位置,但不能凭空出现或消失;
二. 动态神经辐射场
D-Nerf 的核心就是建立映射
M
:
(
x
,
d
,
t
)
→
(
c
,
σ
)
\mathcal{M}: (\bold x, \bold d, t) \rightarrow (\bold{c}, σ)
M:(x,d,t)→(c,σ)。将其分解为
Ψ
x
\Psi_x
Ψx 和
Ψ
t
\Psi_t
Ψt 两个映射:
Ψ
x
\Psi_x
Ψx 表示 NeRF 的 标准配置 (canonical configuration),
Ψ
t
\Psi_t
Ψt 表示
t
t
t 时刻的变形场景到标准 NeRF 的 位移 (displacement)。于是,不同时刻的场景间不再独立,而是通过一个标准配置连接起来。

1. 标准网络
标准网络 (Canonical Network) 就是原始的 NeRF:
Ψ
x
(
x
,
d
)
↦
(
c
,
σ
)
\Psi_x(\bold{x}, \bold{d}) \mapsto (\bold{c}, \sigma)
Ψx(x,d)↦(c,σ)
2. 变形网络
变形网络 (Deformation Network) 用于表示
t
t
t 时刻的真实场景到标准网络的位移:
Ψ
t
(
x
,
t
)
=
{
Δ
x
,
if
t
≠
0
0
,
if
t
=
0
\Psi_t(\mathbf{x}, t)= \begin{cases} \Delta \mathbf{x}, & \text { if } t \neq 0 \\ 0, & \text { if } t=0 \end{cases}
Ψt(x,t)={Δx,0, if t=0 if t=0
和 NeRF 中一样,直接使用多层感知机处理输入在生成视图时表现较差。因此标准网络和变形网络的多层感知机都使用 γ ( p ) \gamma(p) γ(p) 进行位置编码。
三. 新视图渲染
同 NeRF,从指定视角
o
\bold{o}
o 发出的方向为
d
\bold{d}
d 的光线,在
h
h
h 时刻能够到达的空间点为:
x
(
h
)
=
o
+
h
d
\bold{x}(h)=\bold{o}+h \bold{d}
x(h)=o+hd
t
t
t 时刻观察到像素点
p
p
p 的颜色为:
C
(
p
,
t
)
=
∫
h
n
h
f
T
(
h
,
t
)
σ
(
p
(
h
,
t
)
)
c
(
p
(
h
,
t
)
,
d
)
d
h
C(p, t)=\int_{h_n}^{h_f} \mathcal{T}(h, t) \sigma(\mathbf{p}(h, t)) \mathbf{c}(\mathbf{p}(h, t), \mathbf{d}) d h
C(p,t)=∫hnhfT(h,t)σ(p(h,t))c(p(h,t),d)dh
其中:
p
(
h
,
t
)
=
x
(
h
)
+
Ψ
t
(
x
(
h
)
,
t
)
[
c
(
p
(
h
,
t
)
,
d
)
,
σ
(
p
(
h
,
t
)
)
]
=
Ψ
x
(
p
(
h
,
t
)
,
d
)
T
(
h
,
t
)
=
exp
(
−
∫
h
n
h
σ
(
p
(
s
,
t
)
)
d
s
)
\mathbf{p}(h, t)=\mathbf{x}(h)+\Psi_t(\mathbf{x}(h), t) \\ [\mathbf{c}(\mathbf{p}(h, t), \mathbf{d}), \sigma(\mathbf{p}(h, t))]=\Psi_x(\mathbf{p}(h, t), \mathbf{d})\\ \mathcal{T}(h, t)=\exp \left(-\int_{h_n}^h \sigma(\mathbf{p}(s, t)) d s\right)
p(h,t)=x(h)+Ψt(x(h),t)[c(p(h,t),d),σ(p(h,t))]=Ψx(p(h,t),d)T(h,t)=exp(−∫hnhσ(p(s,t))ds)
分层采样后使用离散积分方法进行累加:
C
′
(
p
,
t
)
=
∑
n
=
1
N
T
′
(
h
n
,
t
)
α
(
h
n
,
t
,
δ
n
)
c
(
p
(
h
n
,
t
)
,
d
)
C^{\prime}(p, t)=\sum_{n=1}^N \mathcal{T}^{\prime}\left(h_n, t\right) \alpha\left(h_n, t, \delta_n\right) \mathbf{c}\left(\mathbf{p}\left(h_n, t\right), \mathbf{d}\right)
C′(p,t)=n=1∑NT′(hn,t)α(hn,t,δn)c(p(hn,t),d)
其中:
α
(
h
,
t
,
δ
)
=
1
−
exp
(
−
σ
(
p
(
h
,
t
)
)
δ
)
T
′
(
h
n
,
t
)
=
exp
(
−
∑
m
=
1
n
−
1
σ
(
p
(
h
m
,
t
)
)
δ
m
)
δ
n
=
h
n
+
1
−
h
n
\alpha(h, t, \delta)=1-\exp (-\sigma(\mathbf{p}(h, t)) \delta)\\ \mathcal{T}^{\prime}\left(h_n, t\right)=\exp \left(-\sum_{m=1}^{n-1} \sigma\left(\mathbf{p}\left(h_m, t\right)\right) \delta_m\right)\\ \delta_n=h_{n+1}-h_n
α(h,t,δ)=1−exp(−σ(p(h,t))δ)T′(hn,t)=exp(−m=1∑n−1σ(p(hm,t))δm)δn=hn+1−hn
四. 实验结果
1. 实验细节
同 NeRF,训练过程中使用小批量随机梯度下降,损失函数为真实像素和生成像素的均方误差:
L
=
1
N
s
∑
i
=
1
N
s
∥
C
^
(
p
,
t
)
−
C
′
(
p
,
t
)
∥
2
2
\mathcal{L}=\frac{1}{N_s} \sum_{i=1}^{N_s}\left\|\hat{C}(p, t)-C^{\prime}(p, t)\right\|_2^2
L=Ns1i=1∑Ns
C^(p,t)−C′(p,t)
22
2. 数据集
- Hell Warrior:
- Mutant:
- Hook:
- Bouncing Balls:
- Lego:
- T-Rex:
- Stand Up:
- Jumping Jacks:
3. 实验效果

如图所示,第 1 行分别展示了 Mutant 和 Stand Up 数据集下的标准网络(即
t
=
0
t = 0
t=0)的新视图生成,从左到右分别是:渲染的 RGB 图像、三维网格表示的体积密度、深度图表示的体积密度、变形场表示的位移。第 2 ~ 4 行分别表示了时间累计下(即
t
=
0.5
t = 0.5
t=0.5 和
t
=
1
t = 1
t=1)的视图渲染情况。

文章还通过实验回答了 D-NeRF 如何建模阴影的效果 2,即模型如何编码同一个点的外观变化。如图绘制了在特定时刻的标准网络和真实场景之间的对应点对,D-NeRF 能够通过扭曲标准网络来合成阴影效果。
4. 对比实验

5. 副产品
五. 总结
D-NeRF 最大的创新点是可以建模移动或变形物体组成的动态场景。
D-NeRF 的缺点主要有两个:相机观测位置需要人工标注(同 NeRF);时间变量带来的变形导致模型无法收敛。
六. 复现
论文笔记:D-NeRF:Neural Radiance Fields for Dynamic Scenes ↩︎
论文随记|D-NeRF: Neural Radiance Fields for Dynamic Scenes
↩︎