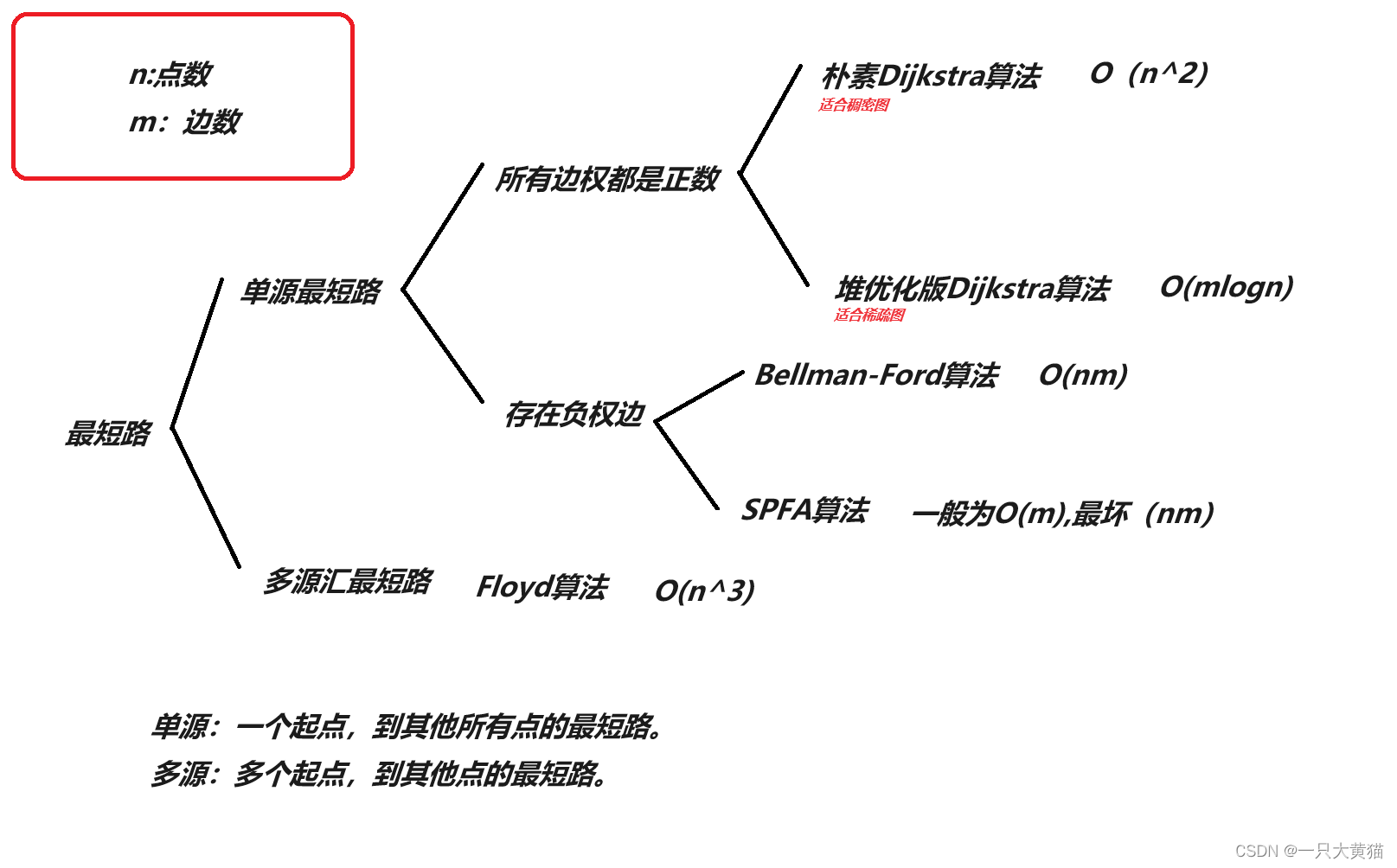
最短路问题基础问题到这里就结束了，附上最短路问题知识结构图。

题目

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环，边权可能为负数。

再给定 k 个询问，每个询问包含两个整数 x 和 y，表示查询从点 x 到点 y 的最短距离，如果路径不存在，则输出 impossible。

数据保证图中不存在负权回路。

输入格式

第一行包含三个整数 n,m,k。

接下来 m 行，每行包含三个整数 x,y,z，表示存在一条从点 x 到点 y 的有向边，边长为 z。

接下来 k 行，每行包含两个整数 x,y，表示询问点 x 到点 y 的最短距离。

输出格式

共 k 行，每行输出一个整数，表示询问的结果，若询问两点间不存在路径，则输出 impossible。

数据范围

1 ≤ n ≤ 200
1 ≤ k ≤ n^2
1 ≤ m ≤ 20000
图中涉及边长绝对值均不超过 10000

思路

    十分暴力，使用二维数组d储存点i到点j的最短距离。最外层循环是k，第二层是i，最内层是j，表示的是所有点i通过点k到达点j，取最小值存入d[i][j]中。

代码

#include<bits/stdc++.h>
#define int long long
#define  N 210
#define INF 1000000000
#define S "impossible"
using namespace std;

int n,m,Q;// n点数，m边数，Q询问次数
int d[N][N];// 储存点i到点j的最短距离

void floyd()
{
    for(int k = 1; k <= n; k ++)
        for(int i = 1; i <= n; i ++)
            for(int j = 1; j <= n; j ++)
                d[i][j] = min(d[i][j],d[i][k] + d[k][j]);// 使用三重循环，保留点i到点j的最小距离
}

int32_t main()
{
    cin >> n >> m >> Q;// 输入点数，边数询问次数
    for(int i = 1; i <= n; i ++)// 初始化一个点到另一个点的距离
        for(int j = 1; j <= n; j ++)
            if(i == j) d[i][j] = 0;// 一个点到它本身的距离为0
            else d[i][j] = INF;// 将点i到点j的距离初始化为INF
    while(m --)
    {
        int a,b,w;
        cin >> a >> b >> w;
        d[a][b] = min(d[a][b],w);// 存在重边的话，保留长度最小的边
    }
    floyd();
    while(Q --)
    {
        int a,b;
        cin >> a >> b;
        if(d[a][b] < INF / 2)// 如果点a可以到达点b则输出最短距离，否则输出impossible
            cout << d[a][b] << endl;
        else
            cout << S << endl;
    }
    return 0;
}