一、背景

在一个页面中需要实现两个Form表单，并在页面提交时需要对两个Form表单进行校验，两个表单都校验成功时才能提交

所用技术栈：Vue2+Element UI

二、实现效果

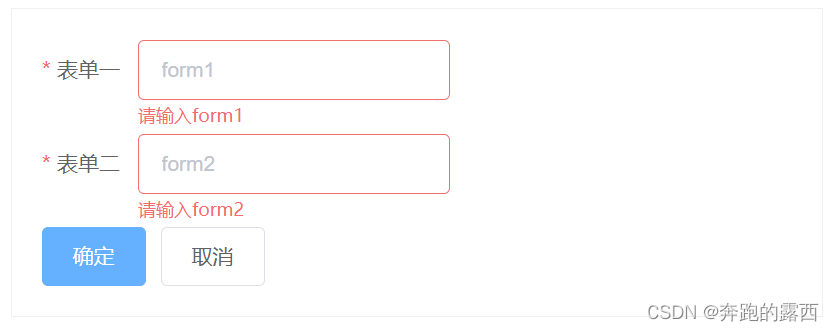
三、多个表单验证

注意项：

两个form表单，每个表单上都设置单独的model和ref，不能同时使用，否则每个表单上的校验提示会失效

<template>
  <div>
    <!-- 表单一区域 -->
    <el-form :inline="true" :model="form1Mode" class="demo-form-inline" ref="form1Ref" :rules="form1Rules">
      <el-form-item label="表单一" prop="user">
        <el-input v-model="form1Mode.user" placeholder="form1"></el-input>
      </el-form-item>
    </el-form>
    <!-- 表单二区域 -->
    <el-form :inline="true" :model="form2Mode" class="demo-form-inline" ref="form2Ref" :rules="form2Rules">
      <el-form-item label="表单二" prop="user">
        <el-input v-model="form2Mode.user" placeholder="form2"></el-input>
      </el-form-item>
    </el-form>
    <!-- 按钮提交区域 -->
    <div>
      <el-button type="primary" @click="onSubmit">确定</el-button>
      <el-button>取消</el-button>
    </div>
  </div>
</template>

3.1、方式一：依次对两个表单进行校验

<script>
export default {
  data() {
    return {
      form1Mode: {
        user: ''
      },
      form2Mode: {
        user: ''
      },
      form1Rules: {
        user: [{ required: true, message: '请输入form1', trigger: 'blur' }]
      },
      form2Rules: {
        user: [{ required: true, message: '请输入form2', trigger: 'blur' }]
      }
    }
  },
  methods: {
    //确定按钮
    async onSubmit() {
      try {
        await this.$refs.form1Ref.validate()
        console.log('表单1校验通过')
        await this.$refs.form2Ref.validate()
        console.log('表单2校验通过')
        //都校验成功之后，这里可以发请求
        this.$message.success('表单校验成功')
      } catch (error) {
        console.error('表单校验失败', error)
      }
    }
  }
}
</script>

3.2、方式二：两个表单同时校验------使用Promise.all

<script>
export default {
  data() {
    return {
      form1Mode: {
        user: ''
      },
      form2Mode: {
        user: ''
      },
      form1Rules: {
        user: [{ required: true, message: '请输入form1', trigger: 'blur' }]
      },
      form2Rules: {
        user: [{ required: true, message: '请输入form2', trigger: 'blur' }]
      }
    }
  },
  methods: {
    //封装验证函数
    submitForm(formUser) {
      return new Promise((resolve, reject) => {
        this.$refs[formUser].validate((valid) => {
          if (valid) {
            resolve()
          } else {
            reject(new Error('错误'))
          }
        })
      })
    },
    //确定按钮
    onSubmit() {
      Promise.all([this.submitForm('form1Ref'), this.submitForm('form2Ref')])
        .then(() => {
          //验证成功后在此处发请求
          this.$message.success('验证通过')
        })
        .catch(() => {
          this.$message.error('验证失败')
        })
    }
  }
}
</script>