目录
编辑
前言:
题目一:《消失的数字》
1.先排序再遍历
2.异或
3.等差数列求和,再相减
题目二:《轮转数组》
1.开辟新的数组
2.原地逆序
题目三:《移除元素》
题目四:《删除有序数组的重复项》
题目五:关于时间复杂度的好题分析
总结:
前言:
本专栏每周都会有,用来记录自己这一周学习刷到的好题目,以及自己做错和理解错的题目。并且加以监督自己!!!
本文题目主要来自Leecode的OJ题,接下来我们来一道一道分析。。。
题目一:《消失的数字》
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台

对于该题目,我们将给出三种解法进行讲解。
1.先排序再遍历
int missingNumber(int* nums, int numsSize)
{
//先进行冒泡排序
for(int i = 0;i<numsSize - 1;i++)
{
for(int j = 0;j<numsSize - i - 1;j++)
{
if(nums[j] > nums[j+1])
{
int tmp = nums[j+1];
nums[j+1] = nums[j];
nums[j] = tmp;
}
}
}
//遍历数组,再返回
int i = 0;
for(i = 0;i < numsSize; i++)
{
if(nums[i] != i)
{
return i;
}
}
return i;
}
该算法是最简单的方法,其中因为要进行冒泡排序,所以该算法的时间复杂度为O(N^2)
本题的代码思路和实现较为简单,在这里我不做过多的赘述。
只是该算法效率很低,
2.异或
int missingNumber(int* nums, int numsSize)
{
int sum = 0;
//0——numsSize进行异或得到sum
for (int i = 0; i < numsSize + 1; i++)
{
sum ^= i;
}
//sum与nums[0——numsSize-1]进行异或,剩下的值就是消失的数字
for (int i = 0; i < numsSize; i++)
{
sum ^= nums[i];
}
return sum;
}我们先简单了解了解异或这个概念。
所谓异或,就是相同为0,相异为1。
那么对于第一个循环,得到sum可以这样理解:

因为异或是可以实现交换律的,即3^5^4 == 3^5^4是一样的。
那么对于第二个循环的实现,可以这样理解:

由此一来就可以得到sum,也就可以得到消失的数字2。
该算法的时间复杂度为O(N) 。
3.等差数列求和,再相减
int missingNumber(int* nums, int numsSize)
{
int sum = ((0 + numsSize)*(numsSize + 1)) / 2;//等差求和
for (int i = 0; i < numsSize; i++)
{
sum -= nums[i];//求和完后减去数组中的每一项,剩下的就是消失的数字
}
return sum;
}这种算法相对好理解,其实就是将0——numsSize的等差数列进行求和
再对数组中的各个元素相减,最后相减完的数就是消失的数字。
该算法的时间复杂度为O(N)

题目二:《轮转数组》
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台

对于本道题目,我们将给出两种方法进行讲解。
1.开辟新的数组
void rotate(int* nums, int numsSize, int k){
int tmp[numsSize];
//考虑到k可能大于nusSize,而轮转数组可以理解为一个圆
k = k%numsSize;
int j = k;
//拷贝前numsSize - k 个
for(int i = 0;i<numsSize -k;i++)
{
tmp[j++] = nums[i];
}
//拷贝后k个
j = 0;
for(int i = numsSize - k;i<numsSize;i++)
{
tmp[j++] = nums[i];
}
//将nums进行覆盖
for(int i = 0;i<numsSize;i++)
{
nums[i] = tmp[i];
}
}这个算法很好理解。

该种算法属于是牺牲空间换取时间的做法,时间复杂度为O(N)
2.原地逆序
void reverse(int* nums, int numsSize)
{
int left = 0;
int right = numsSize - 1;
int tmp = 0;
while (left<right)
{
tmp = nums[left];
nums[left] = nums[right];
nums[right] = tmp;
right--;
left++;
}
}
void rotate(int* nums, int numsSize, int k){
k %= numsSize;
reverse(nums, numsSize);//逆序整个数组
reverse(nums + k, numsSize - k);//逆序后k个元素
reverse(nums, k);//逆序前k个元素
}在这里我们就要讲解一下为什么要进行k %= numsSize这个操作。
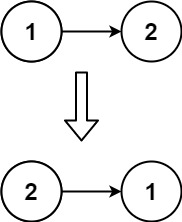
当k == 6的时候,轮转的数组应当是2,3,4,5,6,7,1.
而当k==7时,轮转的数组就是1,2,3,4,5,6,7
又当k == 8时,轮转的数组就是7,1,2,3,4,5,6
所以我们可以看出,k == 7时和 k ==0时没有区别,就像k == 8 与 k == 1没有区别。
因此我们就利用取余操作,来给k赋值,这样可以大大减少程序的计算。
而对于这种算法来说,我们给出以下解释:

该算法的时间复杂度则为O(N)
题目三:《移除元素》
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台

对于该题目,我们要注意的是我们是在空间复杂度为O(1)的情况下完成此题目,意思就是我们不能创建新的临时数组来接受元素并进行判断。
对于这道题目来说,我们可以参考之前讲解的模拟实现strstr来进行编写。
模拟实现strstr的blog如下,需要参考的可以访问以下链接
模拟字符串函数_无双@的博客-CSDN博客
接下来就是本题目的一种算法,采取的是双指针的算法
int removeElement(int* nums, int numsSize, int val){
int right = 0;
int left = 0;
while(right < numsSize)
{
if(nums[right] != val)
{
nums[left++] = nums[right++];
continue;
}
right++;
}
return left;
}该算法时间复杂度为O(N)
具体解法如下图所示

实现循环while(right<numsSize)
在这里我们假设val为2
如果我们nums[right]的值不等于val,将nums[right]的值覆盖到nums[left]
然后两指针都加加,直到如图:

此时直接跳到right++,left不动。
则right会到达

此时就又会进行覆盖操作,即
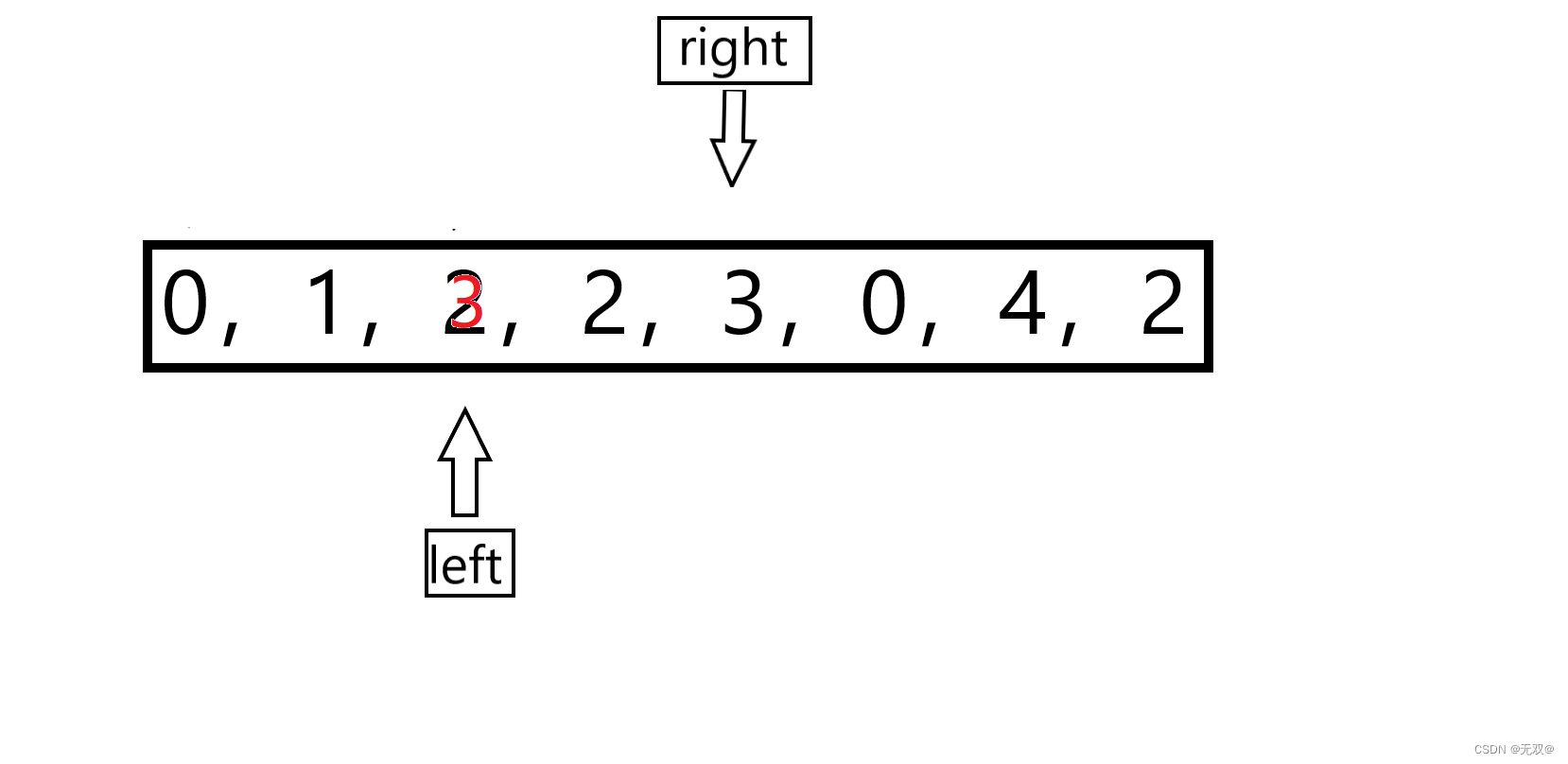
覆盖完后,两个都加加,则此时继续遍历
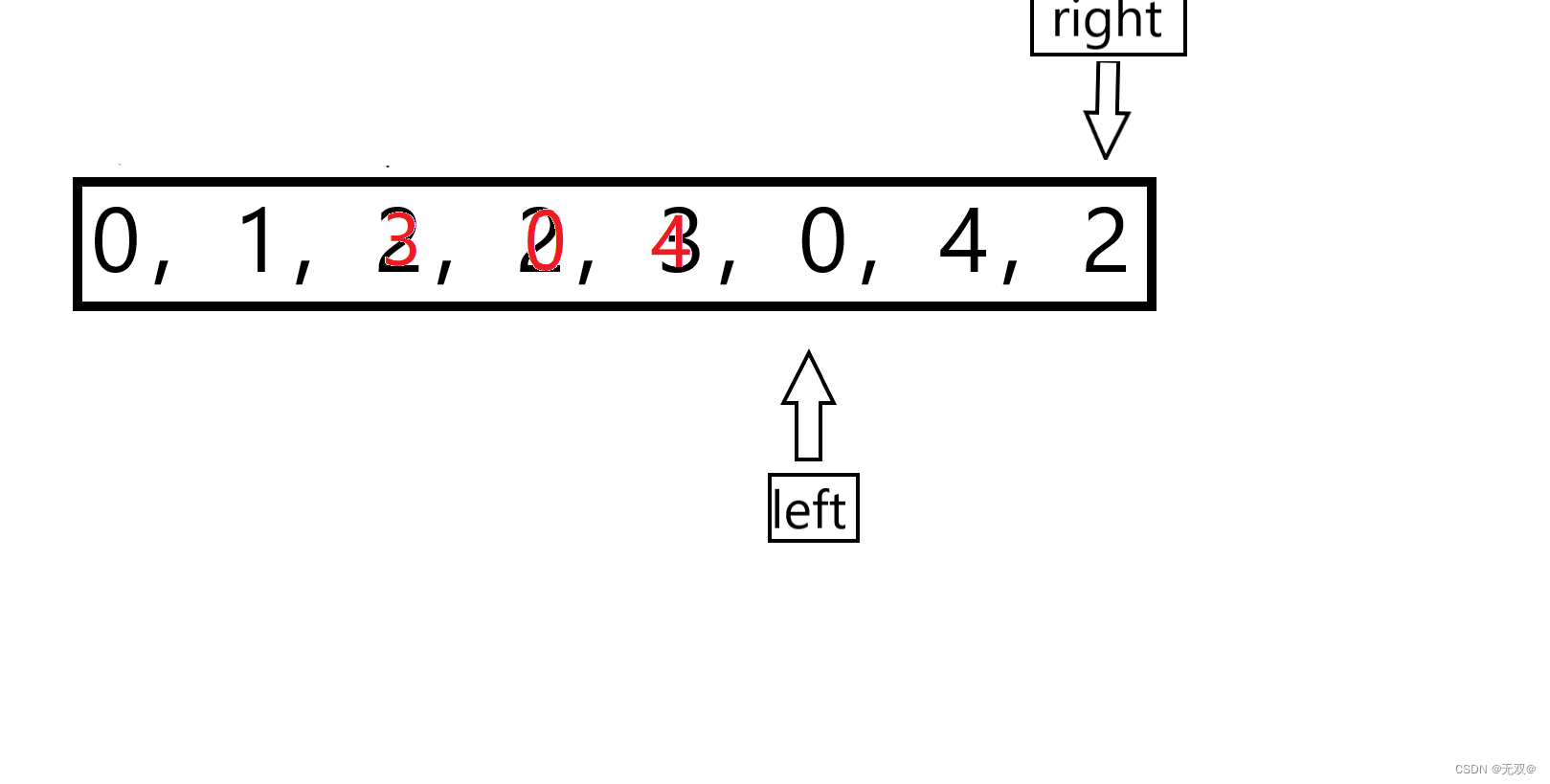
直到出现如图所示的结果,接下来return left,就得到了数组的元素个数,即5。
如此该算法实现完毕
题目四:《删除有序数组的重复项》
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台

对于本题目,我们采取的与上题的算法思路一样,运用双指针的方式来进行实现。
时间复杂度仍然为O(N)
int removeDuplicates(int* nums, int numsSize){
int left = 0;
int right = 0;
while (right<numsSize)
{
if (nums[left] != nums[right])
{
nums[++left] = nums[right];
}
right++;
}
return left + 1;
}对于改题目,讲解如下
刚开始,先定义left和right,指向首元素地址。
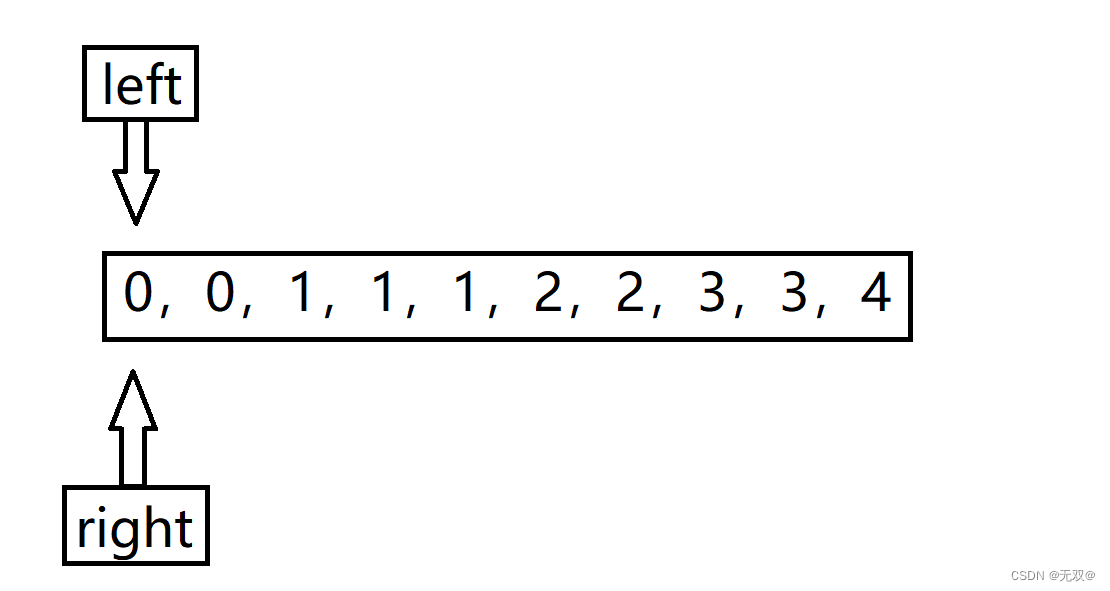
刚开始循环的时候,nums[right]一直== nums[left]
所以right一直++直到,
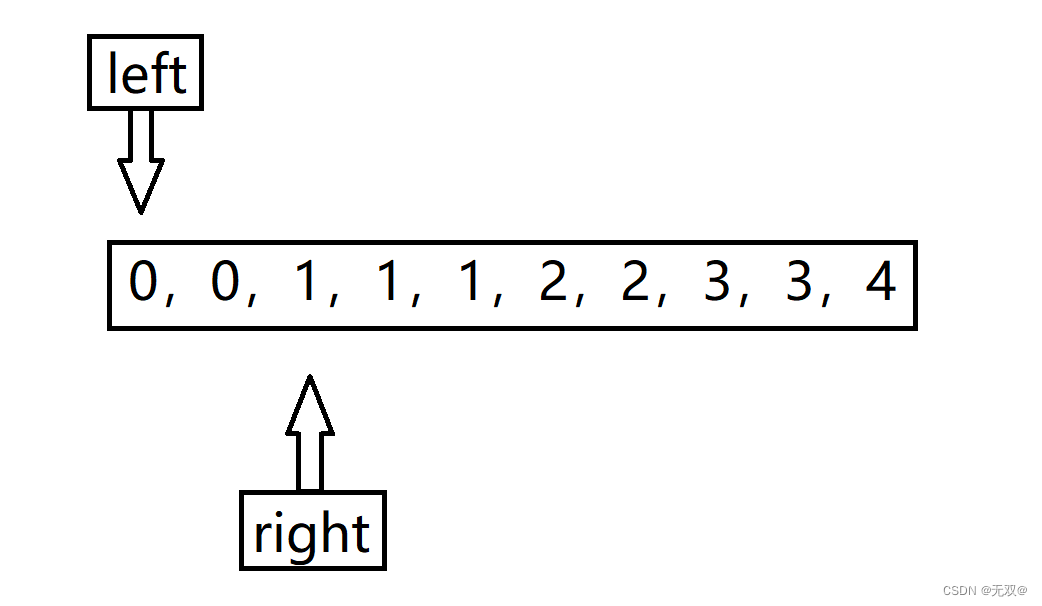
此时进入if语句中,实现覆盖操作:

再接下来,right一直++。

再进行覆盖操作,
然后right继续++。
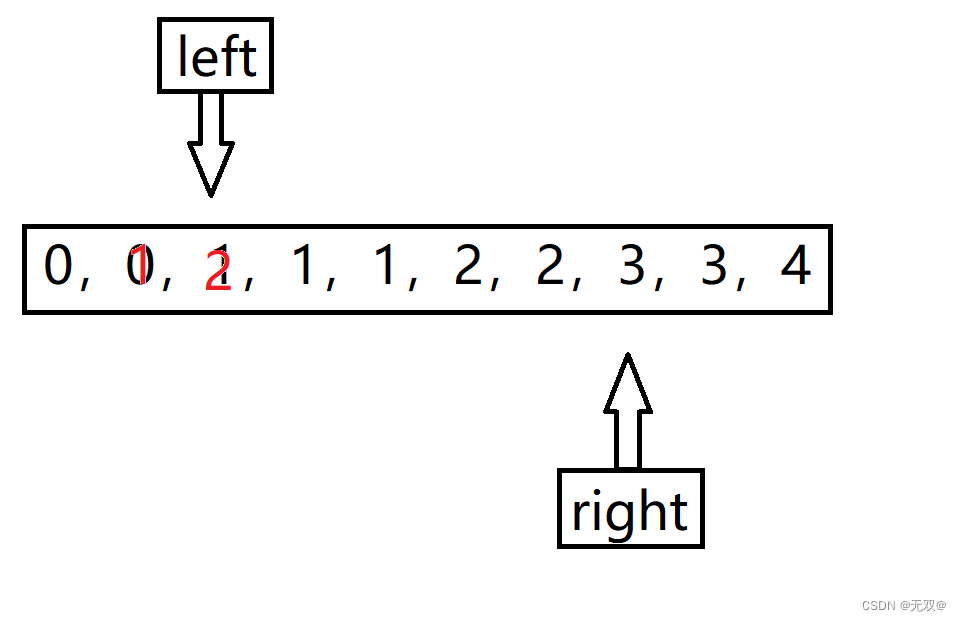
再进行覆盖。
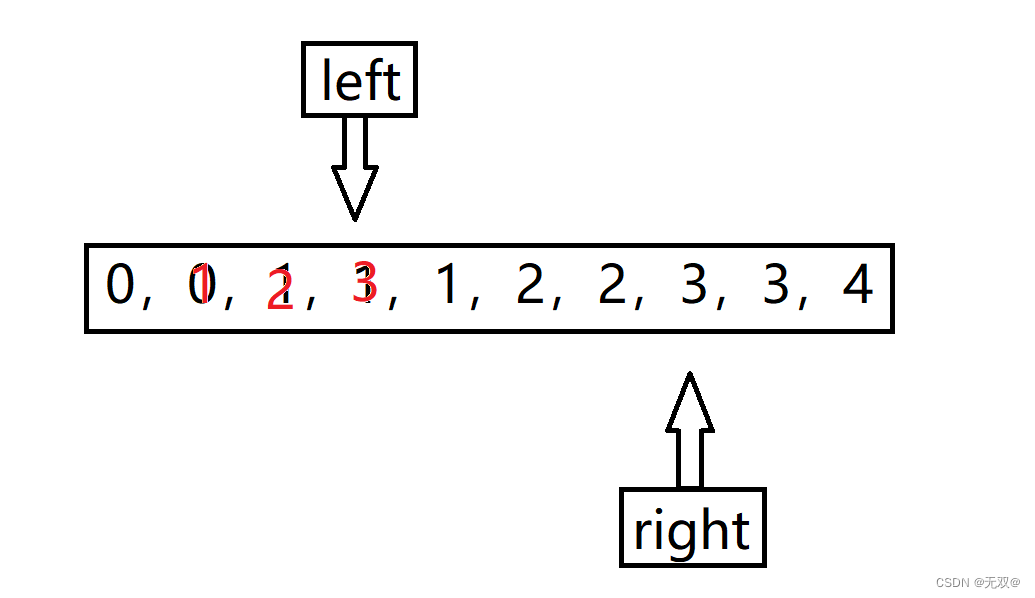
如此就可以得到答案,这就是本算法的基本实现。
这里要注意的是,在覆盖的时候,我们应当先提前对left进行++操作,即前置++。
这样保证left可以先到下一元素,再进行覆盖 。
如果是后置++,则会覆盖上一次覆盖的值。
题目五:关于时间复杂度的好题分析
void fun(int n) {
int i=l;
while(i<=n)
i=i*2;
}求此代码的时间复杂度。
解析: 此函数有一个循环,但是循环没有被执行n次,i每次都是2倍进行递增,所以循环只会被执行log2(n)次。
可以理解为:
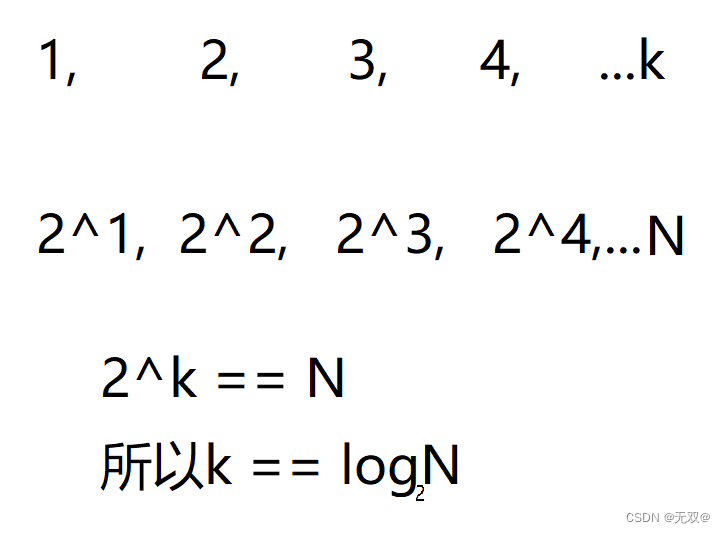
总结:
以上就是本周刷到的好题目。
本文的代码在我的Gitee仓库里:
Leecode_10.22-10.28_CSDN/Leecode_10.22-10.28_CSDN/test_10_28.c · 无双/Data structures amd algorithms - Gitee.com
编程题均来自Leecode,每道题我都有放置网站OJ题,希望大家可以下来做一做。
记住
坐而言不如起而行。
Action speak louder than words!