题目:
如下图所示无向图🐱🐉🐱🐉🐱🐉,其中蓝色边的长度是 1、橘色边的长度是 2、绿色边的长度是 3,求从 'A' 点到 'S' 点的最短距离为多少🤔
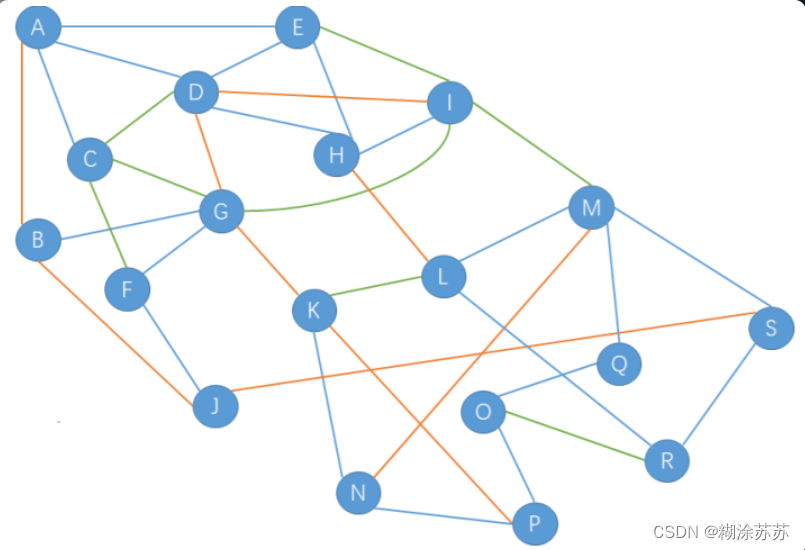
我们得明白一个问题,这个是无向图,python对无向图进行处理的话,可以用到迭代.
迭代和递归区别:
(~ ̄▽ ̄)~所谓迭代,是通过循环重复执行一段代码来解决问题。它通常使用循环结构(如for循环、while循环)来反复执行一组指令,直到达到预定的条件为止。迭代的过程是逐步逼近解决方案,每一次迭代都在上一次的基础上进行操作,直到满足终止条件。
而👀递归是一种通过调用自身来解决问题的方法。递归函数会在执行过程中不断地调用自身🍭🍭🍭,每次调用都会将问题规模缩小,并向基本情况逼近。递归的过程可以看作是将一个大问题分解为多个相同类型的子问题,并通过解决子问题来解决原始问题。
- 首先建立二维列表,对无向图路径及距离进行存储
- 构造函数,对无向图A到S点距离进行统计,并写入到一个列表nums中
- 调用函数,对函数传参
- 打印出nums列表中的最小值,即是从A到S的最短距离
代码如下:
import os
import sys
# 请在此输入您的代码
# list 用来存储无向图的链接数据
list = [
["A", "E", 1],
["A", "B", 2],
["A", "C", 1],
["A", "D", 1],
["B", "G", 1],
["B", "J", 2],
["C", "D", 3],
["C", "G", 3],
["C", "F", 3],
["D", "G", 2],
["D", "H", 1],
["D", "I", 2],
["D", "E", 1],
["E", "H", 1],
["E", "I", 3],
["F", "J", 1],
["F", "G", 1],
["G", "K", 2],
["G", "I", 3],
["H", "L", 2],
["H", "I", 1],
["I", "M", 3],
["J", "S", 2],
["K", "N", 1],
["K", "L", 3],
["K", "P", 2],
["L", "R", 1],
["L", "M", 1],
["M", "N", 2],
["M", "Q", 1],
["M", "S", 1],
["N", "P", 1],
["o", "Q", 1],
["o", "R", 3],
["o", "P", 1],
["R", "S", 1],
]
# nums用来存储起点字母到终点字母的所有路径长度
nums = []
# 定迭代函数获取最短路径
def get(value):
# global 用于在函数内部访问和修改全局变量
global num #num为nums中的元素变量名,代表路径的长度
num += value[2] #将一维列表中代表距离的数值赋值给num并累加
# 遍历无向图list的每一个一维数组
for next_value in list:
# 遍历到S结束循环
# 如果遍历的一维列表中的第二个字符串为S,则满足题意,循环结束
if value[1] == 'S':
nums.append(num)
# break 结束当前循环
break
# 如果下一个列表的第一个字符串=第一个列表的第二个字符串,则进入函数进行迭代
elif next_value[0] == value[1]:
get(next_value)
# 遍历无向图list
for value in list:
# 使起点为A,进入函数计算从A到S的距离
if value[0] == 'A':
# 初始化num为0
num = 0
# 调用定义的函数
get(value)
#打印从起点到终点的最短距离
print(min(nums))