【1739. 放置盒子】

news2024/10/7 6:43:30

来源：力扣（LeetCode）

描述：

有一个立方体房间，其长度、宽度和高度都等于 n 个单位。请你在房间里放置 n 个盒子，每个盒子都是一个单位边长的立方体。放置规则如下：

你可以把盒子放在地板上的任何地方。
如果盒子 x 需要放置在盒子 y 的顶部，那么盒子 y 竖直的四个侧面都必须与另一个盒子或墙相邻。

给你一个整数 n ，返回接触地面的盒子的最少可能数量。

示例 1：

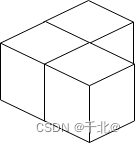
输入：n = 3
输出：3
解释：上图是 3 个盒子的摆放位置。
这些盒子放在房间的一角，对应左侧位置。

示例 2：

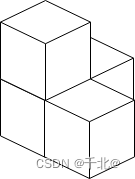
输入：n = 4
输出：3
解释：上图是 3 个盒子的摆放位置。
这些盒子放在房间的一角，对应左侧位置。

示例 3：

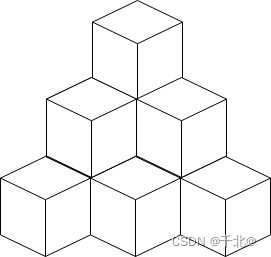
输入：n = 10
输出：6
解释：上图是 10 个盒子的摆放位置。
这些盒子放在房间的一角，对应后方位置。

提示：

1 <= n <= 10⁹

方法：找规律

思路与算法

为了方便画图找规律，我们将立体图转换为平面图来表示：

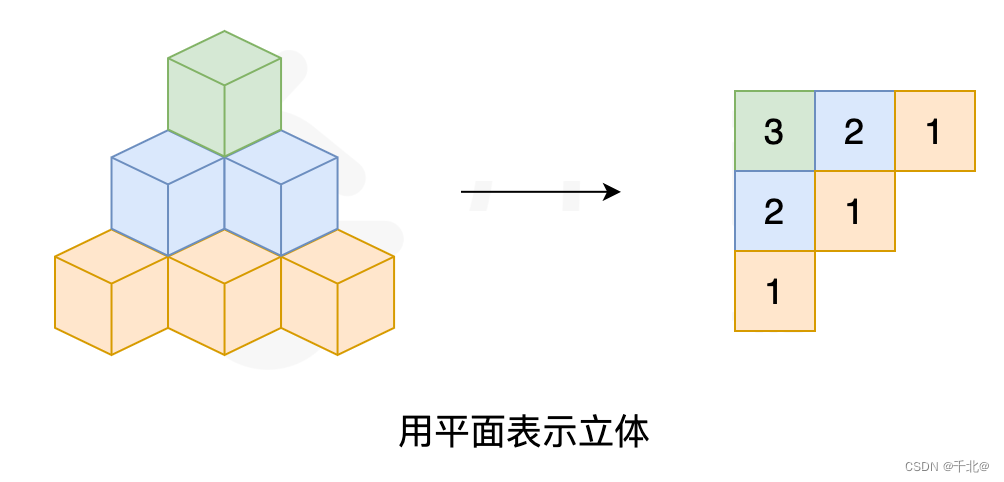
根据贪心思想，接触地面的盒子构成的总体形状应该是一个左上三角，这样才可以使得内部的盒子垒起来的高度更高，以保证接触地面盒子数量最小的情况下容纳更多的盒子。我们画出前四层的盒子增长情况，来试探一下有什么规律存在：

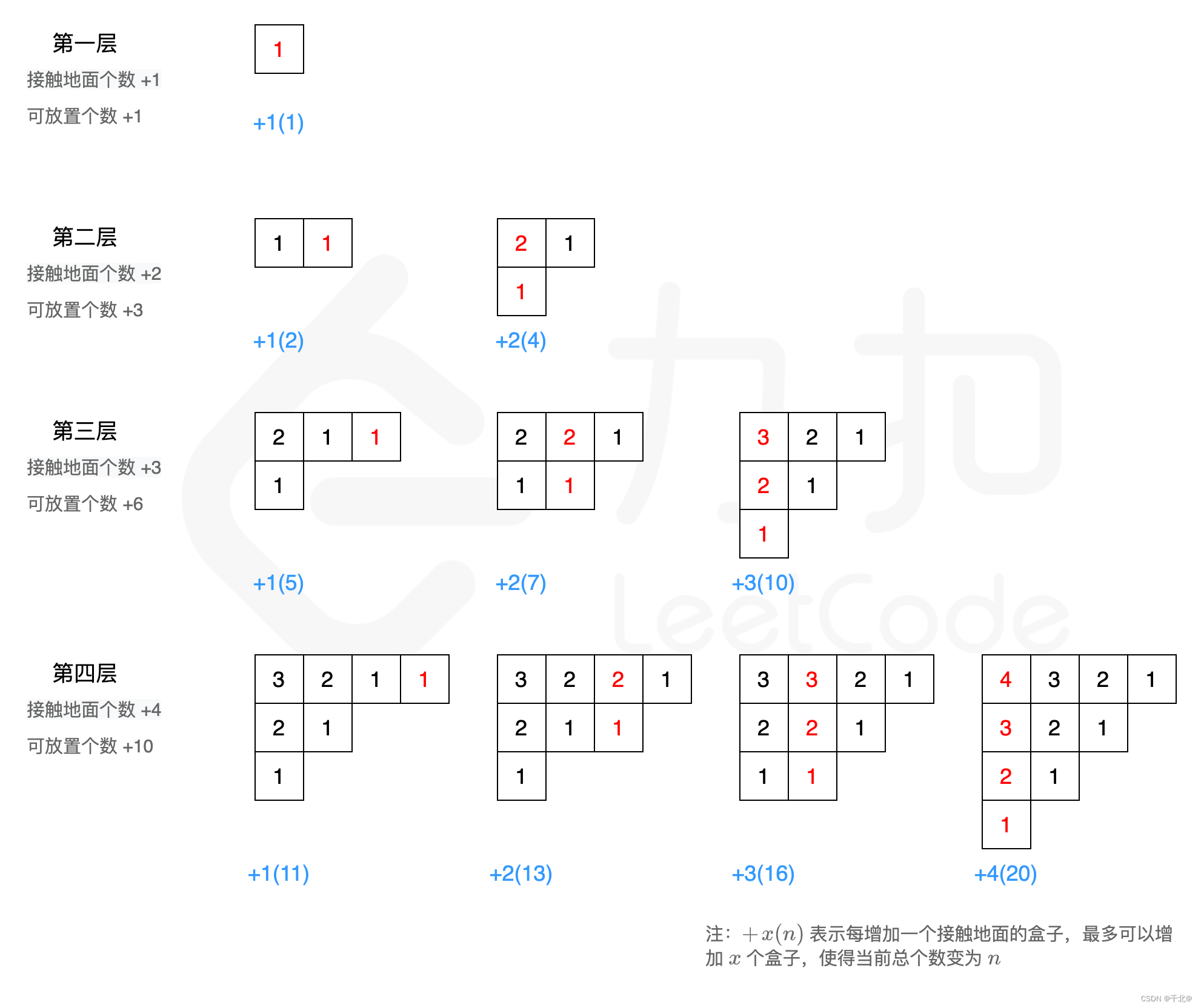
由上图可知，第 i 层最多可以增加 i 个接触地面的盒子，所带来的收益（即增加的盒子放置数）是 (1 + 2 + ⋯ + i) = i × (i + 1) / 2 。随着 i 的增加，成平方级增长。要放置 n 个盒子，我们需要完整的放满 i - 1 层，然后剩余的盒子用第 i 层的 j 个（接触地面的盒子）来填充。

代码：

class Solution {
public:
    int minimumBoxes(int n) {
        int cur = 1, i = 1, j = 1;
        while (n > cur) {
            n -= cur;
            i++;
            cur += i;
        }
        cur = 1;
        while (n > cur) {
            n -= cur;
            j++;
            cur++;
        }
        return (i - 1) * i / 2 + j;
    }
};