之前我们学习过把两个有序数组合并再一起后任然有序，就叫归并；

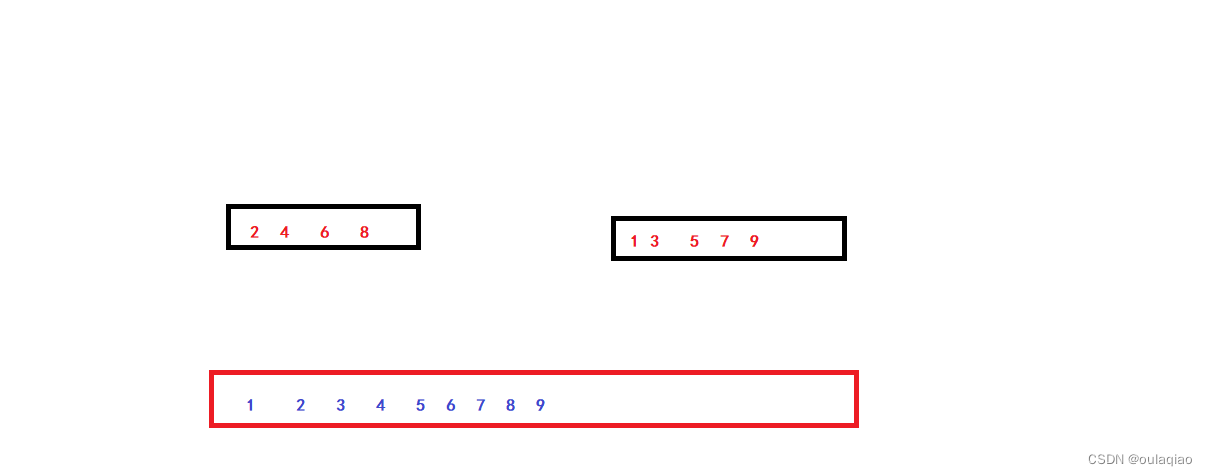
那么，排序是否也可以把一个要排序的数组分割成两个有序的数组，然后归并，之后再拷贝回原数组，就实现了排序
但是怎么才能控制分割成的数组是有序的呢，
当：

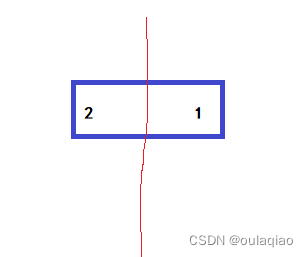
当数组中只有两个数的时候，我们进行分割后，每一个数组就只有一个数，就可以看成有序的

有了这个思想，那么我们就递归分个要排序的数组，当递归分割到只有两个数的时候，在归并

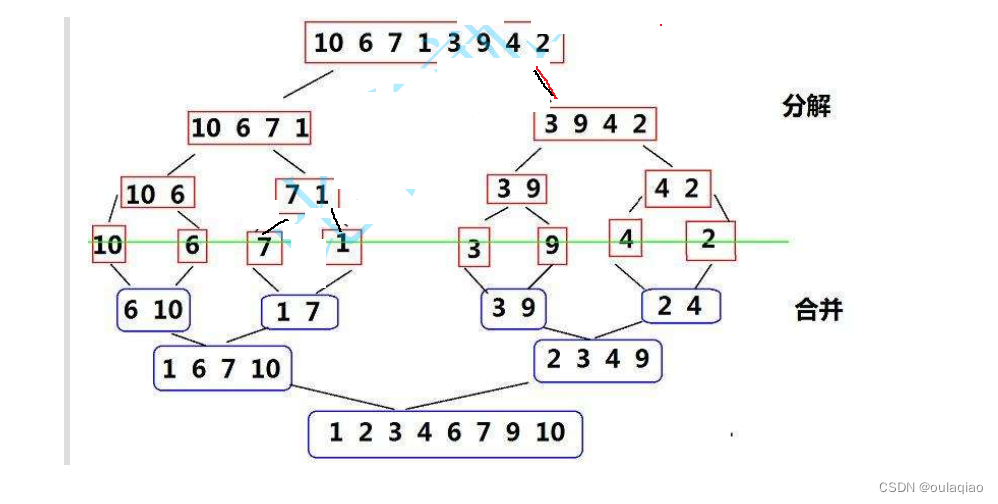
void Merge(int* a, int* tmp, int begin, int end)
{
	//分割
	if (begin == end)
	{
		return;
	}
	int mid = (begin + end) / 2;
	Merge(a, tmp, begin, mid);
	Merge(a, tmp, mid + 1, end);
	//归并
	int begin1 = begin;
	int end1 = mid;
	int begin2 = mid + 1;
	int end2 = end;
	int dex = begin;
	while (begin1<=end1&&begin2<=end2)
	{
		if (a[begin1] <= a[begin2])
		{
			tmp[dex] = a[begin1];
			dex++;
			begin1++;
		}
		else
		{
			tmp[dex] = a[begin2];
			dex++;
			begin2++;
		}
	}
	while (begin1 <= end1)
	{
		tmp[dex] = a[begin1];
		dex++;
		begin1++;
	}
	while (begin2 <= end2)
	{
		tmp[dex] = a[begin2];
		dex++;
		begin2++;
	}
	//拷贝回去
	memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
	

}
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	Merge(a,tmp,0,n-1);
}

非递归的写法：
之前的快速排序是借助栈来实现非递归，因为每次分完之后他就找出了key的位置，那个区间出栈后不需要再用到
但是归并排序的话，分割完后，还要用到之前的分割区间，但是都已经出栈了，就找不到了。所以归并排序的非递归不能用栈来实现

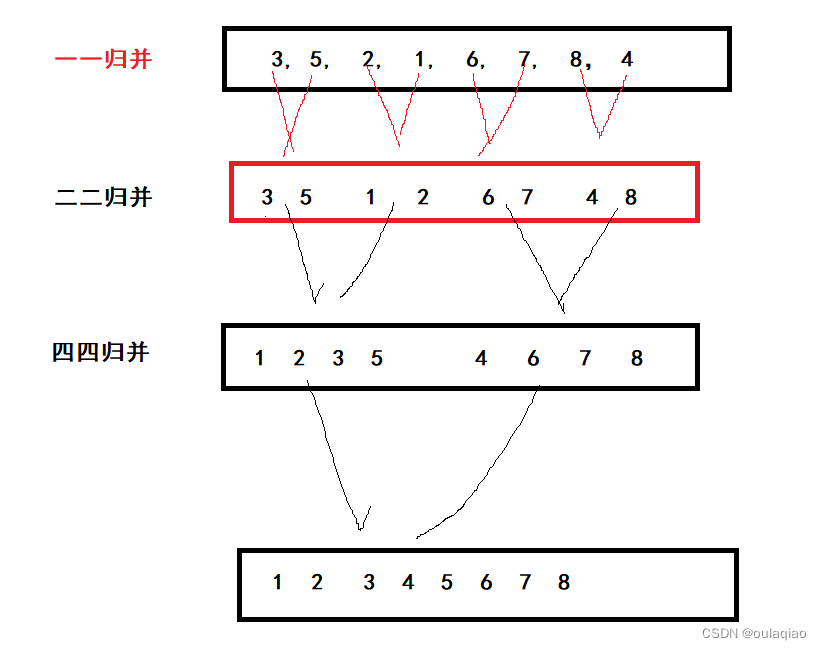
但是这样的归并方式只适合数组中的元素个数是2的指数倍，如果我们要适合其他区任何个数的话在划分区间归并的时候还的判断是否越界

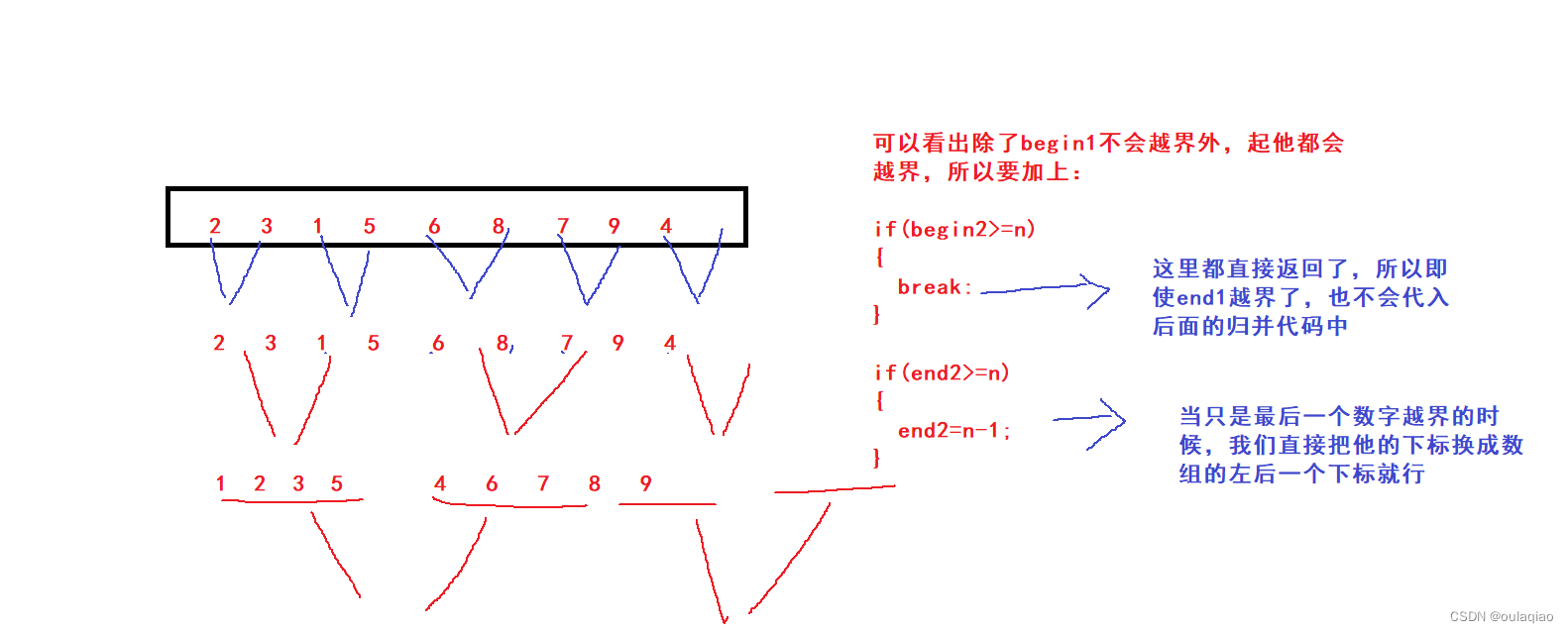
代码：

void MergeSortNoNs(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);

	int pas = 1;
	while (pas<n)
	{
		for (int i = 0; i < n; i += pas * 2)
		{
			int begin1 = i; int end1 = i + pas - 1;
			int begin2 = i + pas; int end2 = i + 2 * pas - 1;
			//越界管理
			if (begin2 >= n)
			{
				break;
			}
			if (end2 >= n)
			{
				end2 = n - 1;
			}
			int dex = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] <= a[begin2])
				{
					tmp[dex] = a[begin1];
					dex++;
					begin1++;
				}
				else
				{
					tmp[dex] = a[begin2];
					dex++;
					begin2++;
				}
			}
			while (begin1 <= end1)
			{
				tmp[dex] = a[begin1];
				dex++;
				begin1++;
			}
			while (begin2 <= end2)
			{
				tmp[dex] = a[begin2];
				dex++;
				begin2++;
			}
			//拷贝回去
			memcpy(a + i, tmp+i, (end2-i+1) * sizeof(int));

		}
		pas *= 2;
	}
}