_15LeetCode代码随想录算法训练营第十五天-C++二叉树
题目列表
- 110.平衡二叉树
- 257.二叉树的所有路径
- 404.左叶子之和
110.平衡二叉树
题目
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
代码
/*
* @lc app=leetcode.cn id=110 lang=cpp
*
* [110] 平衡二叉树
*/
// @lc code=start
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int getHeight(TreeNode* node)
{
if(node == nullptr)
return 0;
int leftH = getHeight(node->left);
int rightH = getHeight(node->right);
//如果左子树不平衡,则返回-1
if(leftH == -1)
return -1;
//如果右子树不平衡,则返回-1
if(rightH == -1)
return -1;
//如果左右子树的高度差大于1,则返回-1
//否则,返回当前node的高度
if(abs(leftH - rightH) > 1)
return -1;
else
return 1 + max(leftH, rightH);
}
bool isBalanced(TreeNode* root) {
if(getHeight(root) == -1)
return false;
else
return true;
}
};
// @lc code=end
257.二叉树的所有路径
题目
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
思路
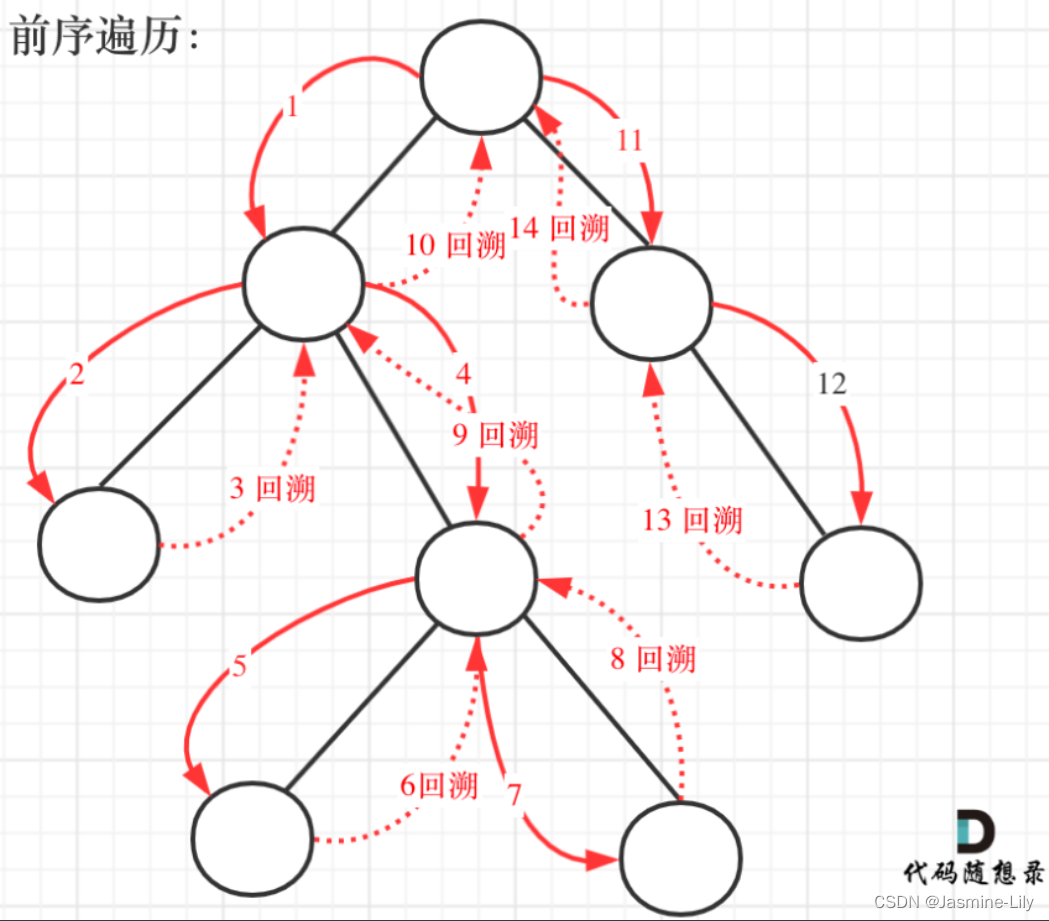
前序遍历,有回溯。
有递归,就有回溯。
代码
递归代码
思路清晰代码
/*
* @lc app=leetcode.cn id=257 lang=cpp
*
* [257] 二叉树的所有路径
*/
// @lc code=start
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void traverse(TreeNode* node, vector<int>& path, vector<string>& res)
{
//中
path.push_back(node->val);
//当node的左孩子和右孩子都为空时,说明遍历到了叶子节点
if(node->left == nullptr && node->right == nullptr)
{
//此时就要将path加入res中
//先将path转换为string
string data;
for(int i = 0; i < path.size() - 1; i++)
{
data += to_string(path[i]);
data += "->";
}
//处理最后一个节点
data += to_string(path[path.size() - 1]);
res.push_back(data);
return;
}
//左
if(node->left != nullptr)
{
traverse(node->left, path, res);//有递归
path.pop_back();//有回溯
}
//右
if(node->right != nullptr)
{
traverse(node->right, path, res);//有递归
path.pop_back();//有回溯
}
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<int> path;
vector<string> res;
if(root == nullptr)
return res;
traverse(root, path, res);
return res;
}
};
// @lc code=end
经典代码
/*
* @lc app=leetcode.cn id=257 lang=cpp
*
* [257] 二叉树的所有路径
*/
// @lc code=start
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
//回溯是通过函数的实参path实现的,此参数不是引用不是指针,因此当递归调用时,使用的是临时变量,
//在本递归中,改变path的值不会改变上一层递归中path的值,由此实现了回溯。
void traversal(TreeNode* cur, string path, vector<string>& result) {
path += to_string(cur->val); // 中
if (cur->left == NULL && cur->right == NULL) {
result.push_back(path);
return;
}
if (cur->left) traversal(cur->left, path + "->", result); // 左
if (cur->right) traversal(cur->right, path + "->", result); // 右
}
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> result;
string path;
if (root == NULL) return result;
traversal(root, path, result);
return result;
}
};
// @lc code=end
非递归代码
/*
* @lc app=leetcode.cn id=257 lang=cpp
*
* [257] 二叉树的所有路径
*/
// @lc code=start
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> res;
//此栈存储TreeNode*
stack<TreeNode*> stTree;
//此栈存储路径
stack<string> stRes;
if(root == nullptr)
return res;
stTree.push(root);
stRes.push(to_string(root->val));
while(!stTree.empty())
{
TreeNode* node = stTree.top();
stTree.pop();
string path = stRes.top();
stRes.pop();
if(node->left == nullptr && node->right == nullptr)
res.push_back(path);
if(node->left != nullptr)
{
stTree.push(node->left);
stRes.push(path + "->" + to_string(node->left->val));
}
if(node->right != nullptr)
{
stTree.push(node->right);
stRes.push(path + "->" + to_string(node->right->val));
}
}
return res;
}
};
// @lc code=end
404.左叶子之和
题目
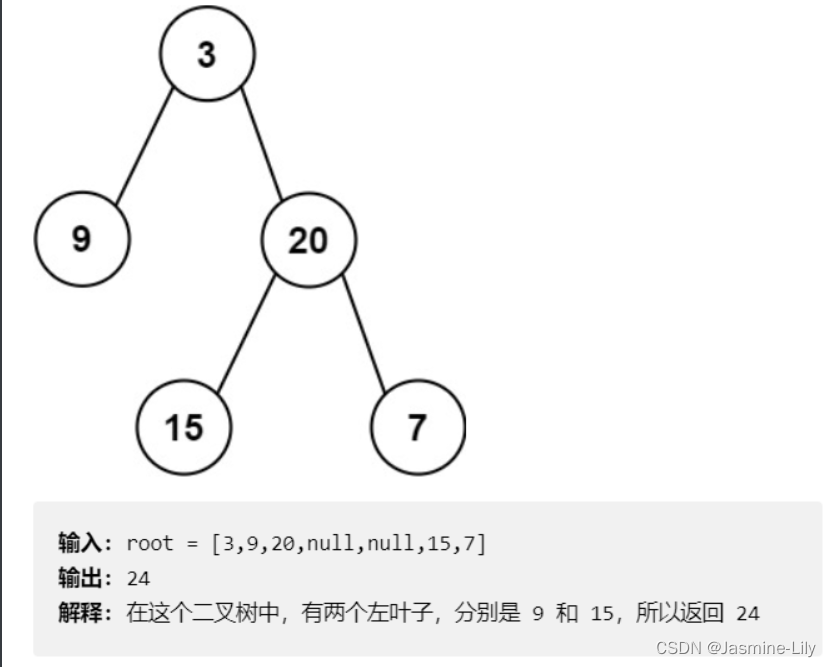
给定二叉树的根节点 root ,返回所有左叶子之和。
整体思路
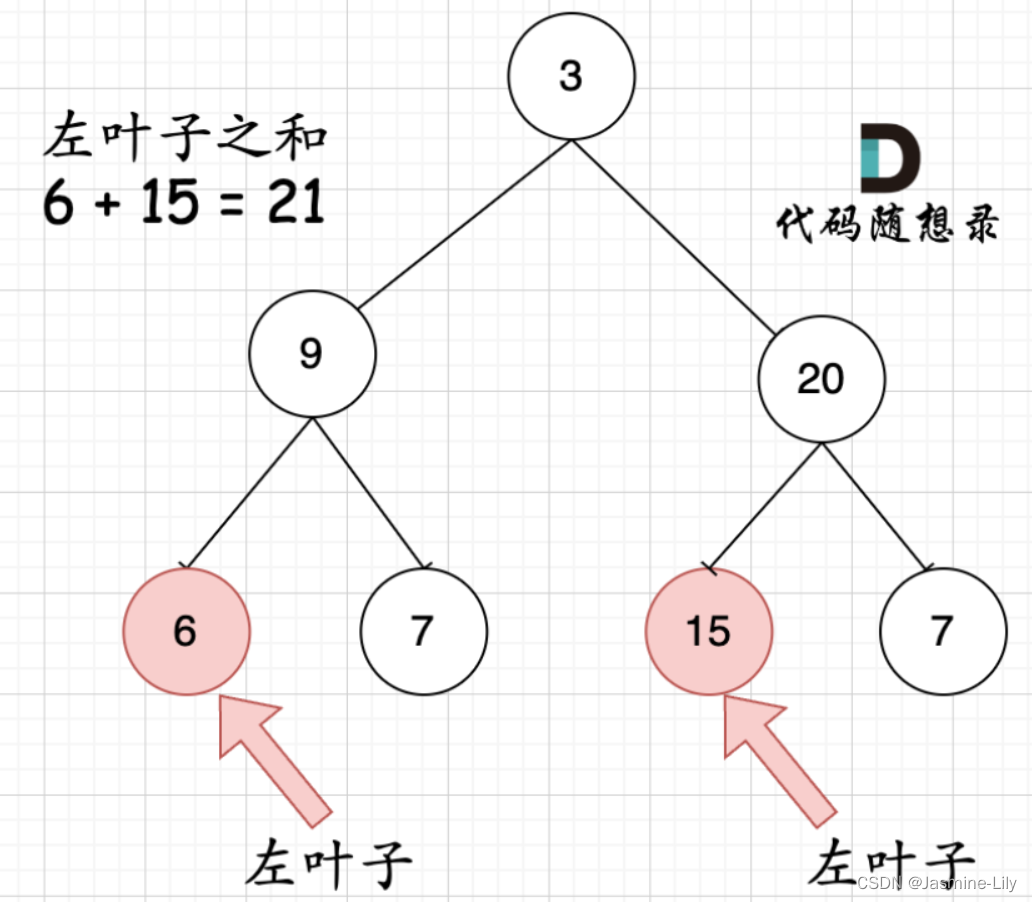
左叶子的明确定义:节点A的左孩子不为空,且左孩子的左右孩子都为空(说明是叶子节点),那么A节点的左孩子为左叶子节点
代码
递归代码
/*
* @lc app=leetcode.cn id=404 lang=cpp
*
* [404] 左叶子之和
*/
// @lc code=start
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//根据父节点判断左孩子是否是左叶子
int sumOfLeftLeaves(TreeNode* root) {
if(root == nullptr)
return 0;
if(root->left == nullptr && root->right == nullptr)
return 0;
//遍历左子树
int leftValue = sumOfLeftLeaves(root->left);
if(root->left != nullptr && root->left->left == nullptr && root->left->right == nullptr)
leftValue = root->left->val;
//遍历右子树
int rightValue = sumOfLeftLeaves(root->right);
return leftValue + rightValue;
}
};
// @lc code=end
非递归代码
/*
* @lc app=leetcode.cn id=404 lang=cpp
*
* [404] 左叶子之和
*/
// @lc code=start
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//根据父节点判断左孩子是否是左叶子
//就是遍历一遍所有元素,然后将需要的元素加起来
int sumOfLeftLeaves(TreeNode* root) {
queue<TreeNode*> que;
int res = 0;
if(root != nullptr)
que.push(root);
while(!que.empty())
{
TreeNode* node = que.front();
que.pop();
if(node->left != nullptr && node->left->left == nullptr && node->left->right == nullptr)
res += node->left->val;
if(node->left != nullptr)
que.push(node->left);
if(node->right != nullptr)
que.push(node->right);
}
return res;
}
};
// @lc code=end




![[Jule CTF 2022] 部分WP](https://img-blog.csdnimg.cn/186abb23f3e348ad8258d965fc97d9bf.png)



![[~/vulhub]/log4j/CVE-2021-44228-20221225](https://img-blog.csdnimg.cn/img_convert/863dd7e2db55cb643e1283a5a8350ec6.png)