红包分配算法
- 错误解法
- 二倍均值法
- JAVA实现
- 线段切割法
- 确定每一条子线段的长度
- JAVA实现
问题如下:
- 所有人抢到的金额之和要等于红包金额,不能多也不能少。
- 每个人至少抢到1分钱。
- 要保证红包拆分的金额尽可能分布均衡,不要出现两极分化太严重的情况。
错误解法
每次拆分的金额 = 随机区间[1分, 剩余金额-1分]
存在的问题:
- 第1个人抢到金额的随机范围是[0.01,99.99]元,在正常的情况下,抢到金额的中位数是50元。假设第1个人随机抢到了50元,那么剩余金额是50元。
- 第2个人抢到金额的随机范围就小得多了,只有[0.01,49.99]元,在正常的情况下,抢到金额的中位数是25元。假设第2个人随机抢到了25元,那么剩余金额是25元。
- 第3个人抢到金额的随机范围就更小了,只有[0,24.99]元,按中位数可以抢到12.5元。
- 以此类推,红包的随机范围将会越来越小,不符合红包拆分的金额尽可能分布均衡的需求。。。
二倍均值法
把每次随机金额的上限定为剩余人均金额的2倍。
红包金额为m元
剩余人数为n
每次抢到的金额 = 随机区间 [0.01,m /n × 2 - 0.01]元
保证了每一次抢到金额随机范围的均值是相等的,不会因为抢红包的先后顺序而造成不公平。
- 第1次随机的金额有一半概率超过20元,使得后面的随机金额上限不足39.99元;
- 第1次随机的金额同样也有一半的概率小于20元,使得后面的随机金额上限超过39.99元。
- 因此从整体来看,第2次随机的平均范围仍然是[0.01,39.99]元。
JAVA实现
/**
* 分配红包的金额
* @param totalAmount 总金额(以分为单位)
* @param totalPeopleNum 总人数
* @return
*/
public static List<Integer> divideRedPackage(Integer totalAmount,Integer totalPeopleNum){
List<Integer> amountList = new ArrayList<Integer>();//存储分配的不同红包大小的数值
Integer restAmount = totalAmount;
Integer restpeopleNum = totalPeopleNum;
Random random = new Random();
//最后一个人不用随机分配了,之间差值
for (int i=0;i<totalPeopleNum-1;i++){
//随机范围:[1,剩余人均金额的2倍-1] 分
//+1d的原因是:random.nextInt随机返回一个值在[0,num)的int类型的整数,包括0不包括num
//random.nextInt+1的范围是[1,num+1)也就是[1,num]
//就满足了随机区间: [1 , m /n × 2 - 1]分
int amount = random.nextInt((restAmount/restpeopleNum)*2-1)+1;
restAmount = restAmount-amount;
restpeopleNum--;
amountList.add(amount);
}
amountList.add(restAmount);
return amountList;
}
测试方法:
public static void main(String[] args) {
List<Integer> amountList = divideRedPackage(1000,10);
for (Integer e:amountList){
System.out.print(e+" ");
}
System.out.println();
}
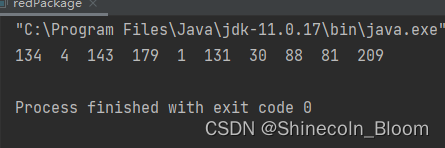
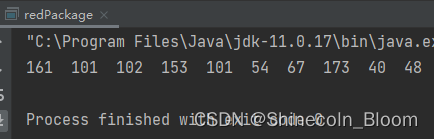
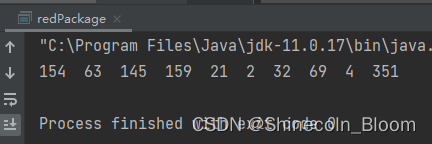
局限性,
除最后一次外,其他每次抢到的金额都要小于剩余人均金额的2倍,并不是完全自由地随机抢红包。(随机数值的上限被限制死了)
线段切割法
把红包总金额想象成一条很长的线段,而每个人抢到的金额,则是这条主线段所拆分出的若干子线段。
确定每一条子线段的长度
由“切割点”来决定。
当n个人一起抢红包时,就需要确定n-1个切割点。
当所有切割点确定以后,子线段的长度也随之确定。此时红包的拆分金额,就等同于每个子线段的长度。
当n个人一起抢总金额为m的红包时,我们需要做n-1次随机运算,以此确定n-1个切割点。
随机的范围区间是[1, m-1]。
开始1和结束是m-1的原因是最少分配1分钱(这里1表示一分)
[0,1]一段,[m-1,m]一段(最小的情况)
需要考虑的问题:
- 当随机切割点出现重复时,如何处理。
- 如何尽可能降低时间复杂度和空间复杂度。
JAVA实现
HashMap和HashSet区别:HashSet存取值
/**
* 拆分红包V2
* @param totalAmount 总金额(以分为单位)
* @param totalPeopleNum 总人数
*/
public static List<Integer> divideRedPackageV2(Integer totalAmount, Integer totalPeopleNum){
List<Integer> amountList = new ArrayList<Integer>();
Set<Integer> segments = new HashSet<Integer>();
Random random = new Random();
for(int i = 0; i< totalPeopleNum-1; i++){
//切割的位置segment,随机的范围区间是[1, m-1]
int segment = random.nextInt(totalAmount-2) + 1;
//delta == 1
int delta = random.nextInt(1)==0 ? 1 : -1;
//这是异常的情况
// segments.contains(segment) ==true 表示切割位置重复
//segment == 0,切割位置不正确
while(segments.contains(segment) || segment == 0){
//加上1位,用来解决以上俩个问题。
//%totalAmount是解决超过线段长度的情况。
segment = (segment+delta)%totalAmount;
}
segments.add(segment);
}
//依据切割的段来划分 钱数
//从HashSet取值
//Collections.sort排序方法,把切割位置从小到大排序。
List<Integer> segmentList = new ArrayList<Integer>(segments);
Collections.sort(segmentList);
for(int i=0; i<segmentList.size(); i++){
Integer amount;
if(i==0){
amount = segmentList.get(0);
}else {
amount = segmentList.get(i) - segmentList.get(i-1) ;
}
amountList.add(amount);
}
amountList.add(totalAmount - segmentList.get(segmentList.size()-1));
return amountList;
}
测试方法:
public static void main(String[] args) {
List<Integer> amountList = divideRedPackageV2(1000,10);
for (Integer e:amountList){
System.out.print(e+" ");
}
System.out.println();
}
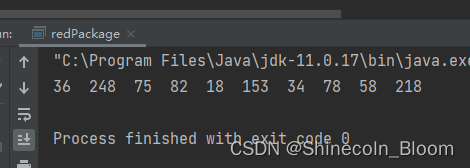
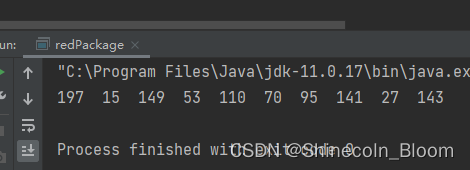
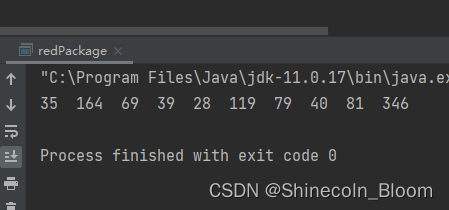
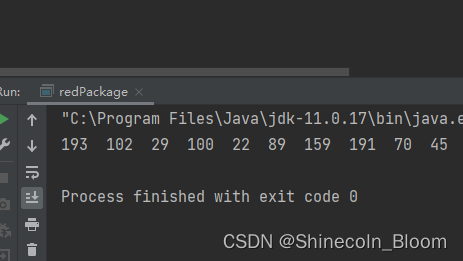
保证了每次划分都是随机,并且概率相同,并且没有最大限制。


![F - Permutation Distance(去绝对值数据结构)[AtCoder Beginner Contest 283]](https://img-blog.csdnimg.cn/65a8ddc7744642f3a0b2652c4a730768.png)
![[CG笔记]绘制图元:三角形](https://img-blog.csdnimg.cn/8b52261f556c42258818dc1f3195802f.png)