文章目录

绘制统计图形
- 1.柱状图
- - 1.1 应用场景--定性数据的分布展示
  - 1.2 绘制原理
- 2.条形图
- 3.堆积图
- - 3.1 堆积柱状图
  - 3.2 堆积条形图
- 4.分块图
- - 4.1 多数据并列柱状图
  - 4.2 多数据平行条形图
- 5.参数探索
- 6.堆积折线图、间断条形图和阶梯图
- - 6.1 用函数stackplot()绘制堆积折线图
  - 6.2 用函数broken_barh()绘制间断条形图
  - 6.3 用函数step()绘制阶梯图
- 7.直方图
- - 7.1 应用场景--定量数据的分布展示
  - 7.2 绘制原理
  - 7.3 直方图和柱状图的关系
  - 7.4 堆积直方图
  - 7.5 直方图的不同形状
- 8.饼图
- - 8.1 应用场景--定性数据的比例展示
  - 8.2 绘制原理
  - 8.3 延伸阅读--非分裂式饼图
  - 8.4 案例--绘制内嵌环形饼图
- 9.箱线图
- - 9.1 应用场景--多组定量数据的分布比较
  - 9.2 绘制原理
  - 9.3 延伸阅读--箱体、箱须、离群值的含义和计算方法
  - 9.4 案例1--水平方向的箱线图
  - 9.5 案例2--不绘制离群值的水平箱线图
- 10.误差棒图
- - 10.1 应用场景--定量数据误差范围
  - 10.2 绘制原理
  - 10.3 案例1--带误差棒的柱状图
  - 10.4 案例2--带误差棒的条形图
  - 10.5 案例3--带误差棒的多数据并列柱状图
  - 10.6 案例4--带误差棒的堆积柱状图

绘制统计图形

1.柱状图

柱状图是描述统计中使用频率非常高的一种统计图形。它有垂直样式和水平样式两种可视化效果。这里我们主要介绍柱状图的应用场景和绘制原理。

1.1 应用场景–定性数据的分布展示

柱状图主要是应用在定性数据的可视化场景中，或者是离散型数据的分布展示。例如要，一个本科班级的学生的籍贯分布，出国旅游人士的职业分布以及下载一款App产品的操作系统的分布。

1.2 绘制原理

我们以bar()函数的使用方法来讲解柱状图的绘制原理。

import matplotlib.pyplot as plt

x = [1, 2, 3, 4, 5]
y = [6, 10, 4, 5, 1]

plt.bar(x, y, align='center',color='b',tick_label=['A','B','C','D','E'],alpha=0.6)

plt.xlabel('x')
plt.ylabel('y')

plt.grid(True, axis='y', ls=':', color='r', alpha=0.3)

plt.show()

x: 柱状图中的柱体标签值
y: 柱状图中的柱体高度
align: 柱体对齐方式
color: 柱体颜色
tick_label: 刻度标签值
alpha: 柱体的透明度

bar

2.条形图

如果将柱状图中的柱体由垂直方向变成水平方向，柱状图就变成条形图。

import matplotlib.pyplot as plt

x = [1, 2, 3, 4, 5]
y = [6, 10, 4, 5, 1]

plt.barh(x, y, align='center',color='c',tick_label=['A','B','C','D','E'])

plt.xlabel('x')
plt.ylabel('y')

plt.grid(True, axis='x', ls=':', color='r', alpha=0.3)

plt.show()

barh

3.堆积图

谈起堆积图，我们想到的可能是堆叠的积木或是层层垒起的砖块。因此，堆积图顾名思义就是将若干统计图形堆叠起来的统计图形，自然是一种组合式图形。

3.1 堆积柱状图

如果将函数bar()中的参数bottom的取值设定为列表y，列表y1=[2,6,3,8,5]代表另一套数据，函数bar(x,y1,bottom=y,color=‘r’)就会输出堆积柱状图。

import matplotlib.pyplot as plt

x = [1, 2, 3, 4, 5]
y = [6, 10, 4, 5, 1]
y1 = [2, 6, 3, 8, 5]

plt.bar(x, y, align='center', color='#66c2a5', tick_label=['A', 'B', 'C', 'D', 'E'],label='classA')
plt.bar(x, y1, align='center', color='#8da0cb', bottom=y, label='classB')

plt.legend()
plt.xlabel('x')
plt.ylabel('y')

plt.show()

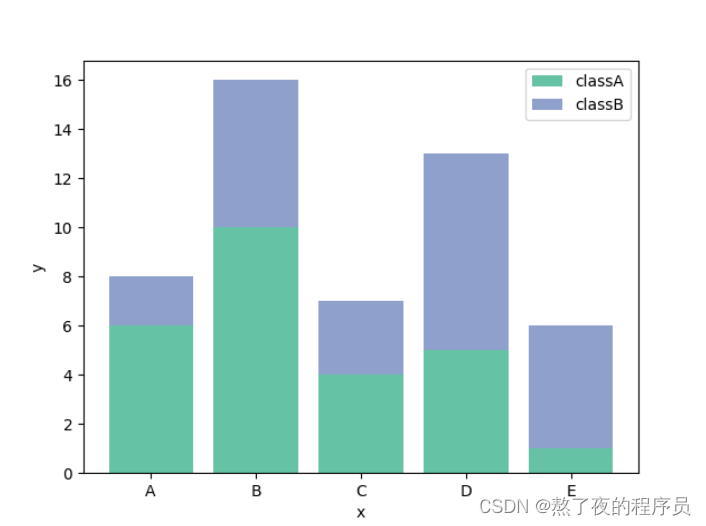
duidie

3.2 堆积条形图

import matplotlib.pyplot as plt

x = [1, 2, 3, 4, 5]
y = [6, 10, 4, 5, 1]
y1 = [2, 6, 3, 8, 5]

plt.barh(x, y, align='center', color='#66c2a5', tick_label=['A', 'B', 'C', 'D', 'E'],label='classA')
plt.barh(x, y1, align='center', color='#8da0cb', left=y, label='classB')

plt.legend()
plt.xlabel('x')
plt.ylabel('y')

plt.show()

duijie

4.分块图

如果我们不将多数据以堆积图的形式进行可视化展示，那么就需要借助分块图来对比多数据的分布差异。同样，分块图可以分为多数据并列柱状图和多数据平行条形图。

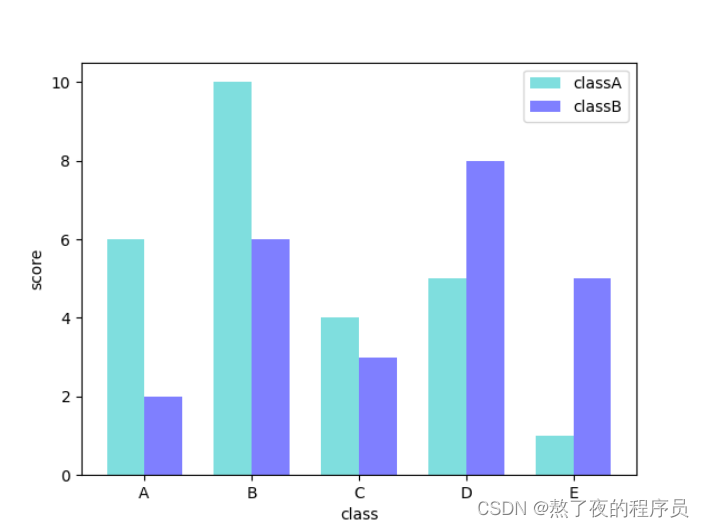
4.1 多数据并列柱状图

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(5)
y = [6, 10, 4, 5, 1]
y1 = [2, 6, 3, 8, 5]

bar_width = 0.35
tick_label = ['A', 'B', 'C', 'D', 'E']

plt.bar(x, y, bar_width, color='c', align='center', label='classA', alpha=0.5)
plt.bar(x+bar_width, y1, bar_width, color='b', align='center', label='classB', alpha=0.5)

plt.xlabel('class')
plt.ylabel('score')

# set xaxis ticks and ticklabels
plt.xticks(x+bar_width/2, tick_label)

plt.legend()

plt.show()

bar

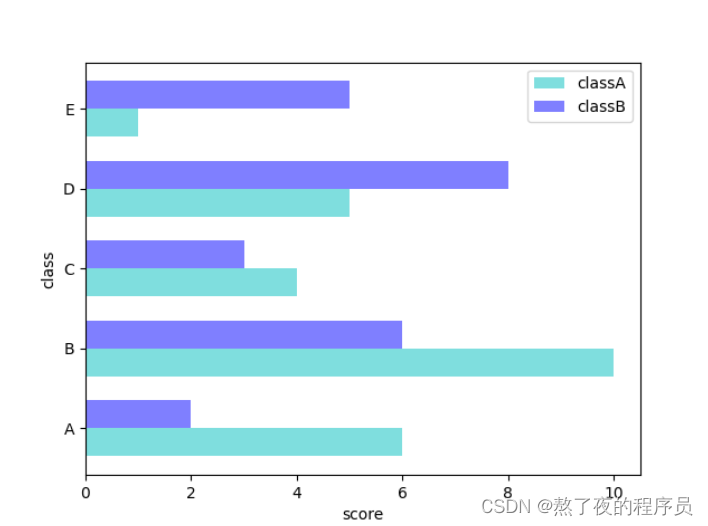
4.2 多数据平行条形图

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(5)
y = [6, 10, 4, 5, 1]
y1 = [2, 6, 3, 8, 5]

bar_width = 0.35
tick_label = ['A', 'B', 'C', 'D', 'E']

plt.barh(x, y, bar_width, color='c', align='center', label='classA', alpha=0.5)
plt.barh(x+bar_width, y1, bar_width, color='b', align='center', label='classB', alpha=0.5)

plt.ylabel('class')
plt.xlabel('score')

# set yaxis ticks and ticklabels
plt.yticks(x+bar_width/2, tick_label)

plt.legend()

plt.show()

barh

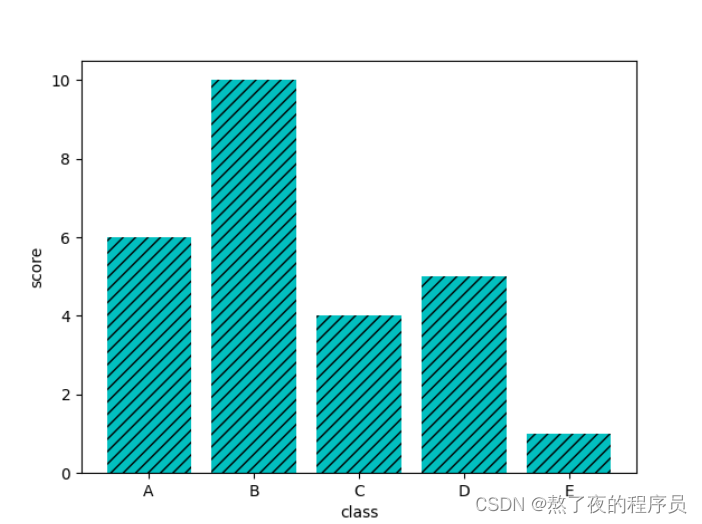
5.参数探索

如果想在柱体上绘制装饰线或装饰图，也就是说，设置柱体的填充样式。我们可以使用关键字参数hatch，该参数可以有很多取值，例如：/ \ | -等，每种符号字符串都是一种填充柱体的几何样式。而且，符号字符串的符号数量越多，柱体的几何图形的密集程度就越高。

import matplotlib.pyplot as plt

x = [1, 2, 3, 4, 5]
y = [6, 10, 4, 5, 1]

plt.bar(x, y, align='center',color='c',tick_label=['A', 'B', 'C', 'D', 'E'],
        hatch='///')

plt.xlabel('class')
plt.ylabel('score')

plt.show()

bar

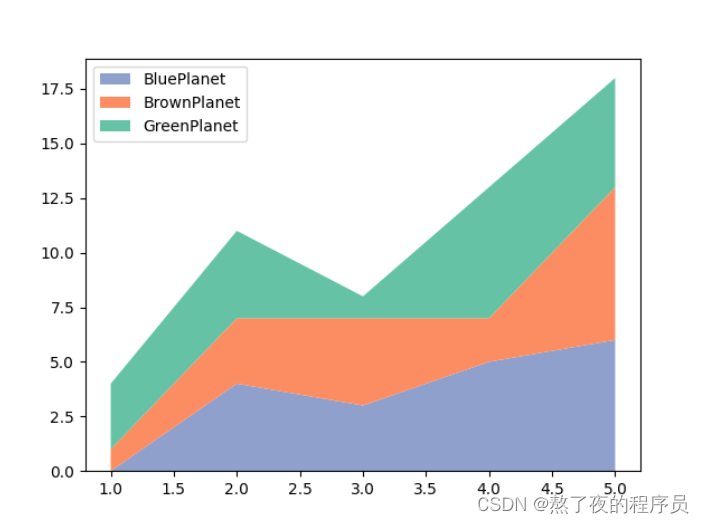
6.堆积折线图、间断条形图和阶梯图

6.1 用函数stackplot()绘制堆积折线图

堆积折线图是通过绘制不同数据集的折线图而生成的。堆积折线图是按照垂直方向上彼此堆叠且又不相互覆盖的排列顺序，绘制若干折线图而形成的组合图形。

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(1, 6, 1)
y = [0, 4, 3, 5, 6]
y1 = [1, 3, 4, 2, 7]
y2 = [3, 4, 1, 6, 5]

labels = ['BluePlanet', 'BrownPlanet', 'GreenPlanet']
colors = ['#8da0cb', '#fc8d62', '#66c2a5']

plt.stackplot(x, y, y1, y2, labels=labels, colors=colors)

plt.legend(loc='upper left')

plt.show()

stackplot

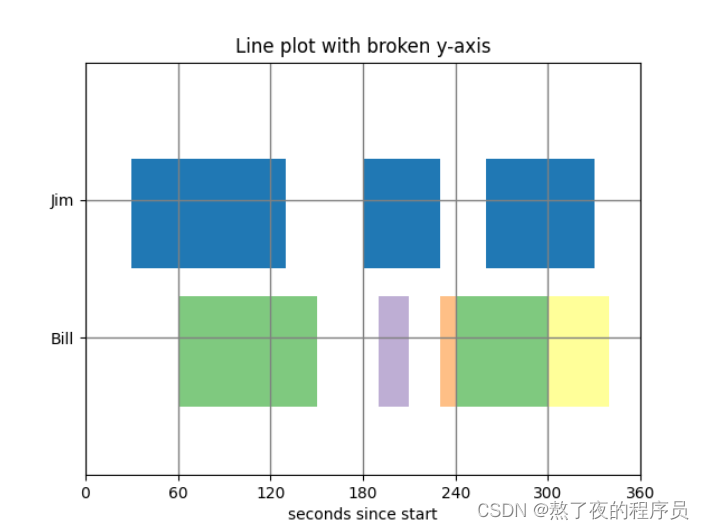
6.2 用函数broken_barh()绘制间断条形图

import matplotlib.pyplot as plt
import numpy as np

plt.broken_barh([(30, 100), (180, 50), (260, 70)], (20, 8), facecolors='#1f78b4')
plt.broken_barh([(60, 90), (190, 20), (230, 30), (280, 60), (240, 60)], (10, 8), facecolors=('#7fc97f',
                '#beaed4', '#fdc086', '#ffff99'))

plt.xlim(0, 360)
plt.ylim(5, 35)
plt.xlabel('seconds since start')

plt.xticks(np.arange(0, 361, 60))
plt.yticks([15, 25], ['Bill', 'Jim'])

plt.grid(ls='-', lw=1, color='gray')

plt.title('Line plot with broken y-axis')
plt.show()

broken_barh

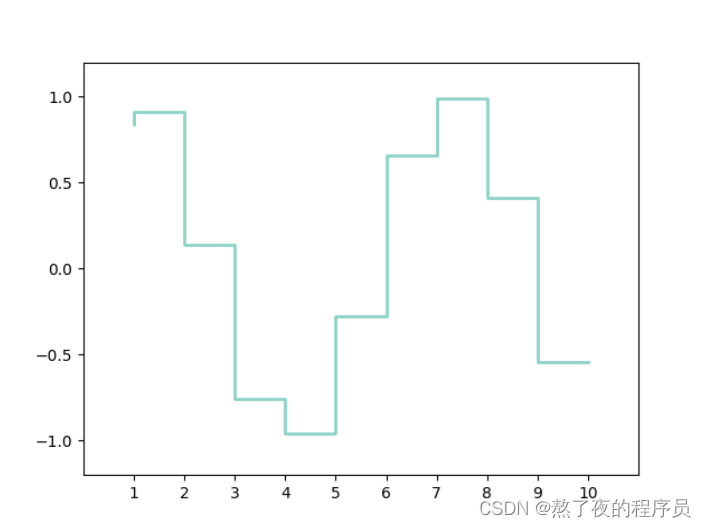
6.3 用函数step()绘制阶梯图

阶梯图在可视化效果上正如图形的名字那样形象，就如同山间的台阶时而上升时而下降，从图形本身而言，很像折线图。也用采是反映数据的趋势变化或是周期规律的。阶梯图经常使用在时间序列数据的可视化任务中，凸显时序数据的波动周期和规律。

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(1, 10, 10)
y = np.sin(x)

plt.step(x, y, color='#8dd3c7', where='pre', lw=2)

plt.xlim(0, 11)
plt.xticks(np.arange(1, 11, 1))
plt.ylim(-1.2, 1.2)

plt.show()

step

7.直方图

直方图是用来展现连续型数据分布特征的统计图形。利用直方图我们可以直观地分析出数据的集中趋势和波动情况。

7.1 应用场景–定量数据的分布展示

直方图主要是应用在定量数据的可视化场景中，或者是用来进行连续型数据的可视化展示。比如，公共英语考试分数的区间分布、抽样调查中的人均寿命的分布特征以及居民可支配收入的分布特征。

7.2 绘制原理

import matplotlib.pyplot as plt
import numpy as np

scoresT = np.random.randint(0, 100, 100)

x = scoresT

bins = range(0, 101, 10)

plt.hist(x, bins=bins, color='#377eb8',
         histtype='bar', rwidth=1.0)

plt.xlabel('Score')
plt.ylabel('Frequency')

plt.show()

hist

x: 连续型数据输入值
bins: 用于确定柱体的个数或是柱体边缘范围
color: 柱体的颜色
histtype: 柱体的类型
label: 图例内容
rwidth: 柱体的相对宽度，取值范围是[0.0, 1.0]

7.3 直方图和柱状图的关系

一方面，直方图和柱状图在展现效果上是非常类似的，只是直方图描述的是连续型数据的分布，柱状图描述的事离散型数据的分布，也可以讲：一个是描述定量数据；另一个是描述定性数据。
另一方面，从图形展示效果来看，柱状图的柱体之间有空隙，直方图的柱体之间没有空隙。

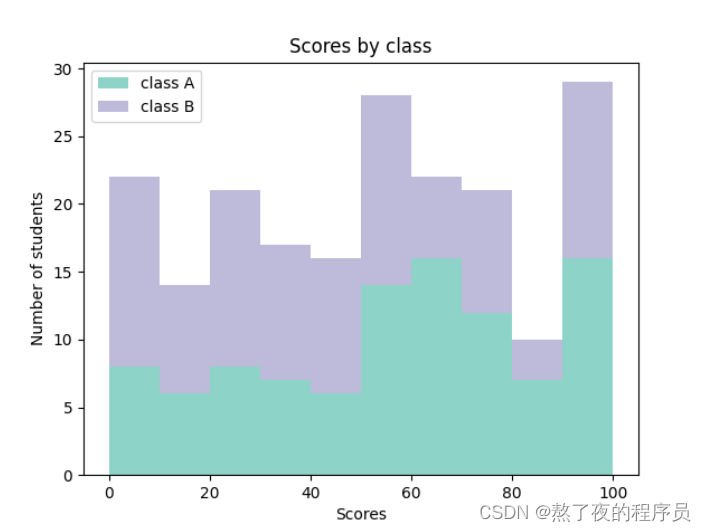
7.4 堆积直方图

import matplotlib.pyplot as plt
import numpy as np

scoresT1 = np.random.randint(0, 100, 100)
scoresT2 = np.random.randint(0, 100, 100)

x = [scoresT1, scoresT2]
colors = ['#8dd3c7', '#bebada']
labels = ['class A', 'class B']

bins = range(0, 101, 10)

plt.hist(x, bins=bins, color=colors,
         histtype='bar', rwidth=1.0,
         stacked=True, label=labels)

plt.xlabel('Scores')
plt.ylabel('Number of students')

plt.title('Scores by class')

plt.legend(loc='upper left')

plt.show()

hist

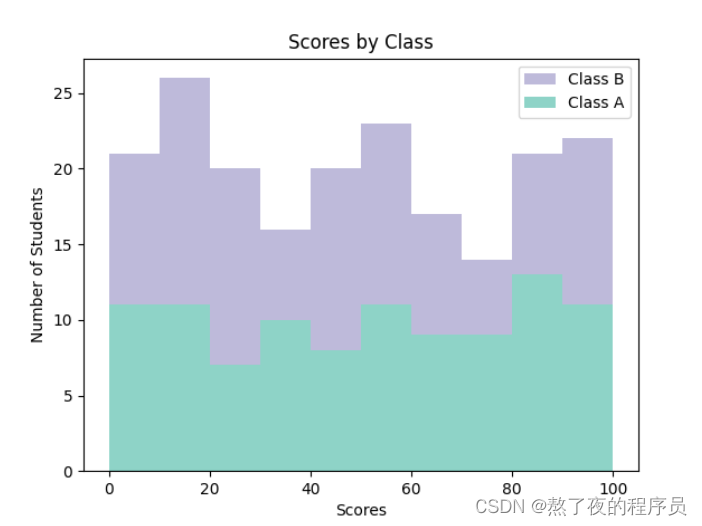
7.5 直方图的不同形状

import matplotlib.pyplot as plt
import numpy as np

scoresT1 = np.random.randint(0, 100, 100)
scoresT2 = np.random.randint(0, 100, 100)

x = [scoresT1, scoresT2]
colors = ['#8dd3c7', '#bebada']
labels = ['Class A', 'Class B']

bins = range(0, 101, 10)

plt.hist(x, bins, histtype='stepfilled', color=colors, label=labels,
         rwidth=1.0, stacked=True)

plt.xlabel('Scores')
plt.ylabel('Number of Students')

plt.title('Scores by Class')

plt.legend()

plt.show()

hist

8.饼图

饼图是用来展示定性数据比例分布特征的统计图形。通过绘制饼图，我们可以清楚地观察出数据的占比情况。

8.1 应用场景–定性数据的比例展示

饼图主要应用在定性数据的可视化场景中，或者是用来进行离散型数据的比例展示。如果需要展示参加硕士研究生考试的性别比例。某市一年中四季使用天然气用量的比重以及家庭生活开支用途的比例分布，这些场景都是使用饼图进行数据可视化的不二之选，通过绘制饼图，就可以直观地反映研究对象定性数据的比例分布情况。

8.2 绘制原理

import  matplotlib.pyplot  as  plt

labels = 'A', 'B', 'C', 'D'

students = [0.35, 0.15, 0.20, 0.30]

colors = ['#377eb8', '#4daf4a', '#984ea3', '#ff7f00']

explode = (0.1, 0.1, 0.1, 0.1)

plt.pie(students, explode=explode, labels=labels, colors=colors, autopct='%3.1f%%', shadow=True, startangle=45)

plt.title('Students')

plt.show()

pie

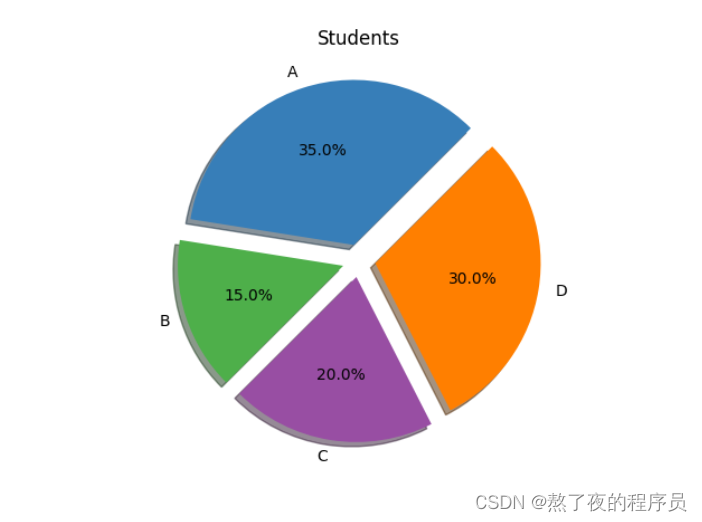
students: 饼片代表的百分比
explode: 饼片边缘偏离半径的百分比
labels: 标记每份饼片的文本标签内容
autopct: 饼片文本标签内容对应的数值百分比样式
startangle: 从x轴作为起始位置，第一个饼片逆时针旋转的角度
shadow: 是否绘制饼片的阴影
colors: 饼片的颜色

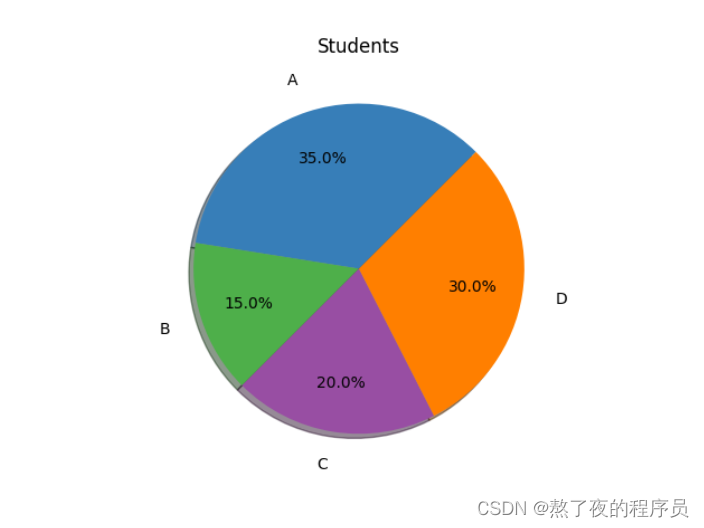
8.3 延伸阅读–非分裂式饼图

import  matplotlib.pyplot  as  plt

labels = 'A', 'B', 'C', 'D'

students = [0.35, 0.15, 0.20, 0.30]

colors = ['#377eb8', '#4daf4a', '#984ea3', '#ff7f00']

plt.pie(students, labels=labels, colors=colors,
        pctdistance=0.7, labeldistance=1.2, autopct='%3.1f%%', shadow=True, startangle=45)

plt.title('Students')

plt.show()

pie

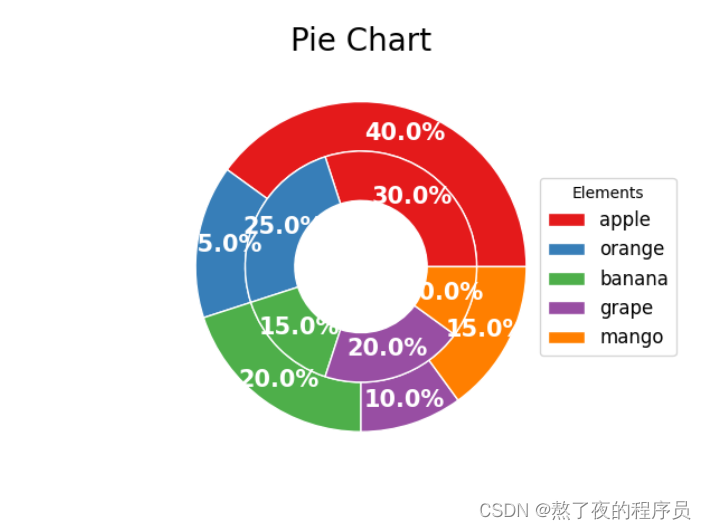
8.4 案例–绘制内嵌环形饼图

饼图不仅可以用来描述定性数据的比例分布，还可以将多个饼图进行嵌套，从而实现内嵌环形饼图的可视化效果。这样，就可以进行多组定性数据比例分布的比较。

import matplotlib.pyplot as plt
import numpy as np

elements = ['apple', 'orange', 'banana', 'grape', 'mango']

weight1 = [40, 15, 20, 10, 15]
weight2 = [30, 25, 15, 20, 10]

colormapList = ['#e41a1c', '#377eb8', '#4daf4a', '#984ea3', '#ff7f00']
outer_colors = colormapList
inner_colors = colormapList

wedges1, texts1, autotexts1 = plt.pie(weight1, radius=1, colors=outer_colors,
                                      autopct='%3.1f%%', pctdistance=0.85, textprops=dict(color="w"),
                                      wedgeprops=dict(width=0.3, edgecolor='w'))

wedges2, texts2, autotexts2 = plt.pie(weight2, radius=0.7, colors=inner_colors,
                                        autopct='%3.1f%%', pctdistance=0.75, textprops=dict(color="w"),
                                        wedgeprops=dict(width=0.3, edgecolor='w'))

plt.legend(wedges1, elements,
           fontsize=12, title="Elements",
           loc="center left", bbox_to_anchor=(0.91, 0, 0.3, 1))

plt.setp(autotexts1, size=15, weight="bold")
plt.setp(autotexts2, size=15, weight="bold")
plt.setp(texts1, size=12)

plt.title("Pie Chart", fontsize=20)

plt.show()

pie

9.箱线图

箱线图是由一个箱体和一对箱须所组成的统计图形。箱体是由第一四分位数、中位数（第二四分位数）和第三四分位数所组成的。在箱须的末端之外的数值可以理解成离群值，因此，箱须是对一组数据范围的大致直观描述。

9.1 应用场景–多组定量数据的分布比较

箱线图主要应用在一系列测量或观测数据的比较场景中，例如学校间或班级间测试成绩的比较，球队中的队员体能对比，产品优化前后的测试数据比较以及同类产品的各项性能的比较，等等，都可以借助箱线图来完成相关分析或研究任务。因此，箱线图的应用范围非常广泛，而且实现起来也非常简单。

9.2 绘制原理

import matplotlib.pyplot as plt
import numpy as np

testA = np.random.randn(5000)
testB = np.random.randn(5000)

testList = [testA, testB]
labels = ['AlphaRM', 'BetaRM']
colors = ['#1b9e77', '#d95f02']

whis = 1.6
width = 0.35

bplot = plt.boxplot(testList, whis=whis, widths=width, sym='o', patch_artist=True, labels=labels)

for patch, color in zip(bplot['boxes'], colors):
    patch.set_facecolor(color)

plt.ylabel('Value')
plt.title('Boxplot of Random Numbers')

plt.grid(axis='y', ls=':', lw=1, color='gray', alpha=0.4)

plt.show()

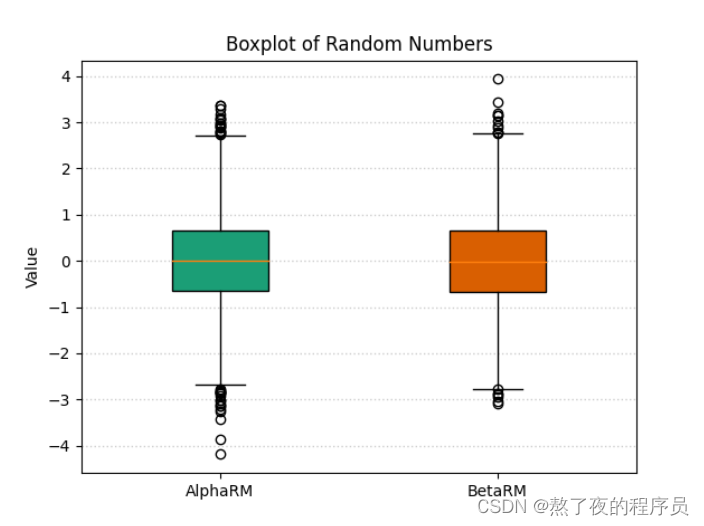
boxplot

testList: 绘制箱线图的输入数据
whis: 四分位间距的倍数，用来确定箱须包含数据的范围的大小
widths: 设置箱体的宽度
sym: 离群值的标记样式
labels: 绘制每一个数据集的刻度标签
patch_artist: 是否给箱体添加颜色

9.3 延伸阅读–箱体、箱须、离群值的含义和计算方法

关于箱线图的组成部分有：箱体、箱须和离群值，其中，箱体主要由第一四分位数、中位数和第三四分位数组成，箱须又分为上箱须和下箱须。下面，介绍一下这些组成部分的含义和计算方法。
上箱须和下箱须长度的确定方法是在绘制箱线图的原始数据集data中分别寻找不大于Q3+whisxIQR的最大值valuemax和不小于Q1-whisxIQR的最小值valuemin，其中Q1和Q3分别是第一四分位数和第三四分位数，whis是关键字参数whis的参数值，IQR(Inter-Quartile Range)是四分位差，计算方法是IQR=Q3-Q1。离群值Outlier的判断标准是value<(Q1-whisxIQR)或者value>(Q3+whisxIQR)，其中，value是数据集data中的数据点。

9.4 案例1–水平方向的箱线图

import matplotlib.pyplot as plt
import numpy as np

x = np.random.randn(1000)

plt.boxplot(x, vert=False)

plt.xlabel('x')
plt.yticks([1], ['AlphaRM'], rotation=90)
plt.title('Boxplot of x')

plt.grid(axis='x', ls=':', lw=1, color='gray', alpha=0.4)

plt.show()

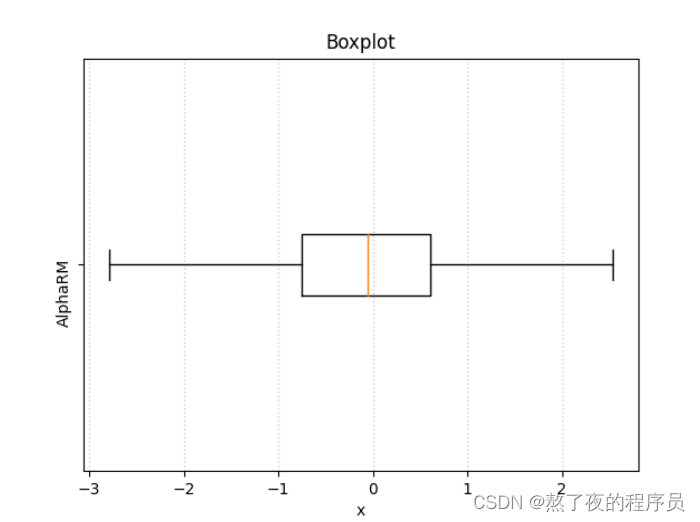
boxplot

9.5 案例2–不绘制离群值的水平箱线图

import matplotlib.pyplot as plt
import numpy as np

x = np.random.randn(1000)

plt.boxplot(x, vert=False, showfliers=False)

plt.xlabel('x')
plt.yticks([1], ['AlphaRM'], rotation=90)
plt.title('Boxplot')

plt.grid(axis='x', ls=':', lw=1, color='gray', alpha=0.4)

plt.show()

boxplot

10.误差棒图

在很多科学实验中都存在测量误差或是试验误差，这是无法控制的客观因素。这样，在可视化试验结果的时候，最好可以给试验结果增加观测结果的误差以表示客观存在的测量偏差。误差棒图就是可以运用在这一场景中的很理想的统计图形。

10.1 应用场景–定量数据误差范围

通过抽样获得样本，对总体参数进行估计会由于样本的随机性导致参数估计值出现波动，因此需要用误差置信区间来表示对总体参数估计的可靠范围。误差棒就可以很好地实现充当总体参数估计的置信区间的角色。误差棒的计算方法可以有很多种：单一数值、置信区间、标准差和标准误等。误差棒的可视化展示效果也有很多种样式：水平误差棒、垂直误差棒、对称误差棒和非对称误差棒等。

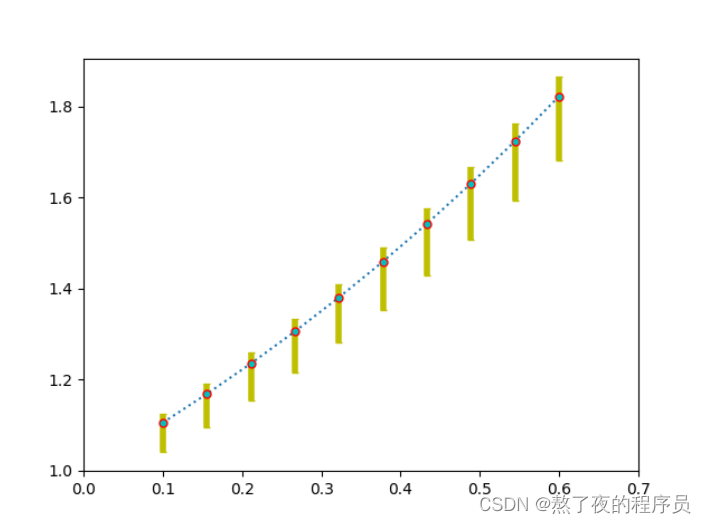
10.2 绘制原理

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0.1, 0.6, 10)
y = np.exp(x)

error = 0.05 + 0.15 * x

lower_error = error
upper_error = 0.3*error
error_limit = [lower_error, upper_error]

plt.errorbar(x, y, yerr=error_limit, fmt=':o',
             ecolor='y', elinewidth=4,
             ms=5,mfc='c',mec='r',
             capthick=1, capsize=2)

plt.xlim(0, 0.7)

plt.show()

errorbar

x,y: 数据点的位置
yerr: 单一数值的非对称形式误差范围
fmt: 数据点的标记样式和数据点标记的连接线样式
ecolor: 误差棒的线条颜色
elinewidth: 误差棒的线条粗细
ms: 数据点的大小
mfc: 数据点的标记颜色
mec: 数据点的标记边缘颜色
capthick: 误差棒边界横杠的厚度
capsize: 误差棒边界横杠的大小

10.3 案例1–带误差棒的柱状图

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(5)
y = [100, 68, 79, 91, 82]
std_err = [7, 2, 6, 10, 5]

error_attri = dict(elinewidth=2, ecolor='black', capsize=3)

plt.bar(x, y, color='c',
        width=0.6, align='center',
        yerr=std_err, error_kw=error_attri,
        tick_label=['A', 'B', 'C', 'D', 'E'])

plt.xlabel('Class')
plt.ylabel('Score')

plt.title('Class Score')

plt.grid(True, axis='y', ls=':', color='gray', alpha=0.2)

plt.show()

bar

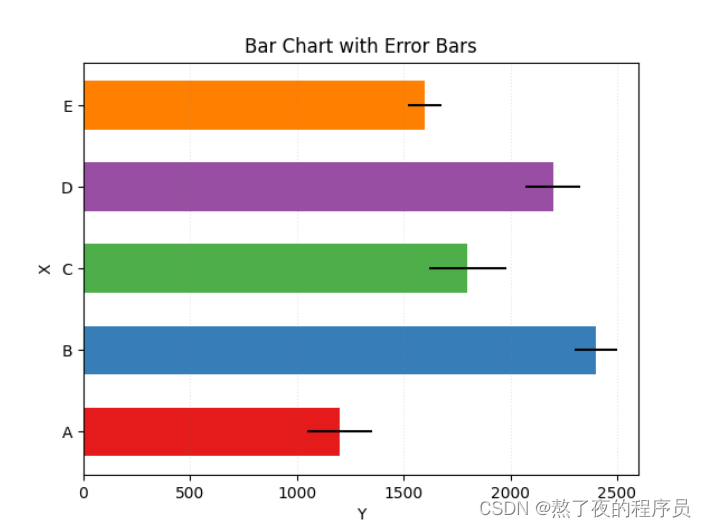
10.4 案例2–带误差棒的条形图

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(5)
y = [1200, 2400, 1800, 2200, 1600]
std_err = [150, 100, 180, 130, 80]

bar_width = 0.6
colors = ['#e41a1c', '#377eb8', '#4daf4a', '#984ea3', '#ff7f00']

plt.barh(x, y, bar_width,
         color=colors, align='center',
         xerr=std_err, tick_label=['A', 'B', 'C', 'D', 'E'])

plt.xlabel('Y')
plt.ylabel('X')

plt.title('Bar Chart with Error Bars')

plt.grid(True, axis='x', ls=':', color='gray', alpha=0.2)

plt.xlim(0, 2600)

plt.show()

bar

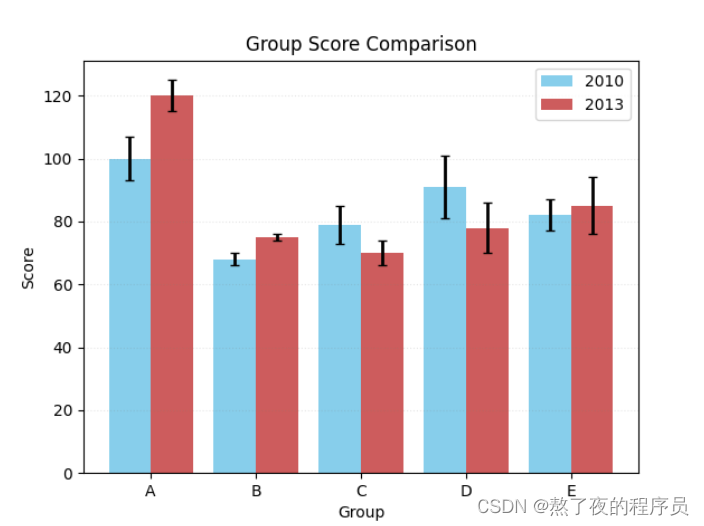
10.5 案例3–带误差棒的多数据并列柱状图

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(5)
y1 = [100, 68, 79, 91, 82]
y2 = [120, 75, 70, 78, 85]
std_err1 = [7, 2, 6, 10, 5]
std_err2 = [5, 1, 4, 8, 9]

error_attri = dict(elinewidth=2, ecolor='black', capsize=3)

bar_width = 0.4
tick_label = ['A', 'B', 'C', 'D', 'E']

plt.bar(x, y1, bar_width,
        color='#87CEEB', align='center',
        yerr=std_err1, error_kw=error_attri,
        label='2010')

plt.bar(x + bar_width, y2, bar_width,
        color='#CD5C5C', align='center',
        yerr=std_err2, error_kw=error_attri,
        label='2013')

plt.xlabel('Group')
plt.ylabel('Score')

plt.xticks(x + bar_width / 2, tick_label)

plt.title('Group Score Comparison')

plt.grid(True, axis='y', ls=':', color='gray', alpha=0.2)

plt.legend()

plt.show()

bar

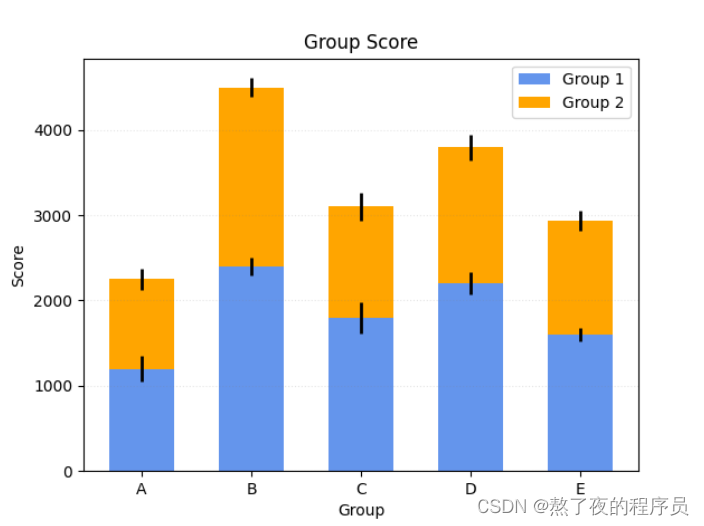
10.6 案例4–带误差棒的堆积柱状图

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(5)
y1 = [1200, 2400, 1800, 2200, 1600]
y2 = [1050, 2100, 1300, 1600, 1340]
std_err1 = [150, 100, 180, 130, 80]
std_err2 = [120, 110, 170, 150, 120]

bar_width = 0.6
tick_label = ['A', 'B', 'C', 'D', 'E']
error_attri = dict(ecolor='black', elinewidth=2, capsize=0)

plt.bar(x, y1, bar_width,
        color='#6495ED', align='center',
        yerr=std_err1, error_kw=error_attri,
        label='Group 1')

plt.bar(x, y2, bar_width,
        bottom=y1, color='#FFA500', align='center',
        yerr=std_err2, error_kw=error_attri,
        label='Group 2')

plt.xlabel('Group')
plt.ylabel('Score')

plt.title('Group Score')

plt.grid(True, axis='y', linestyle=':', color='gray', alpha=0.2)

plt.xticks(x, tick_label)

plt.legend()

plt.show()