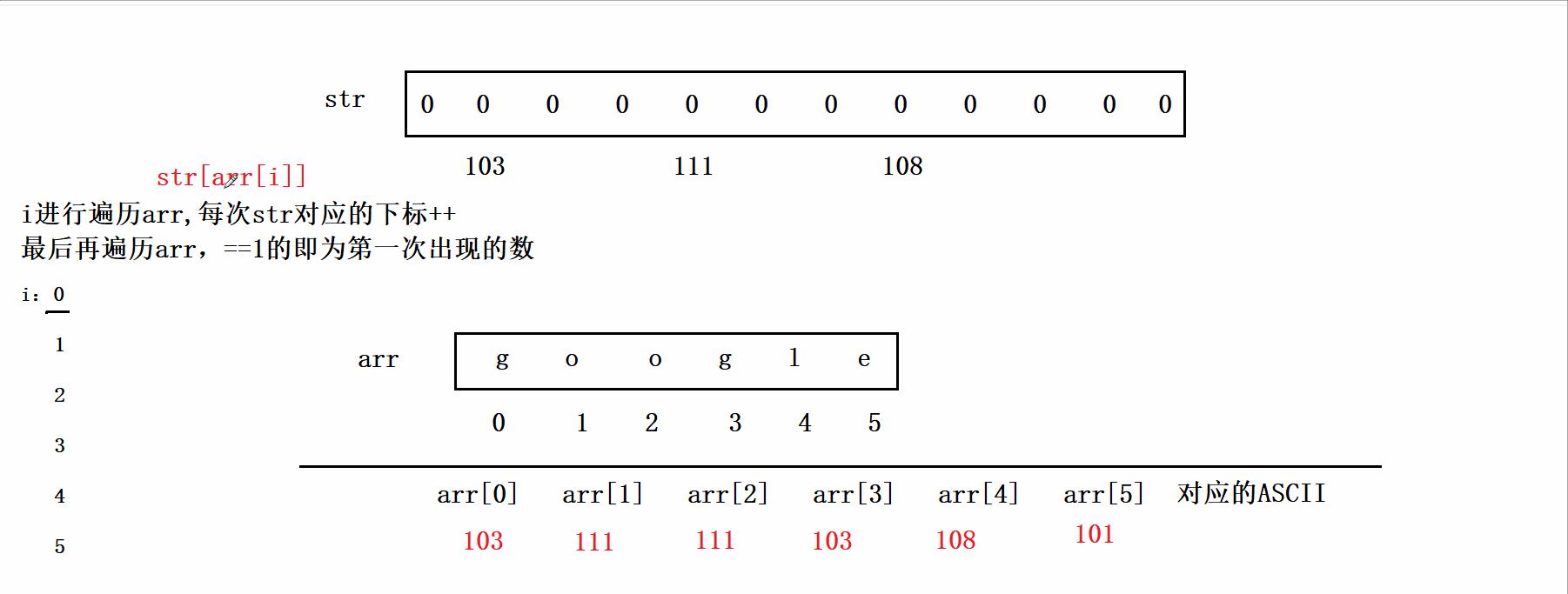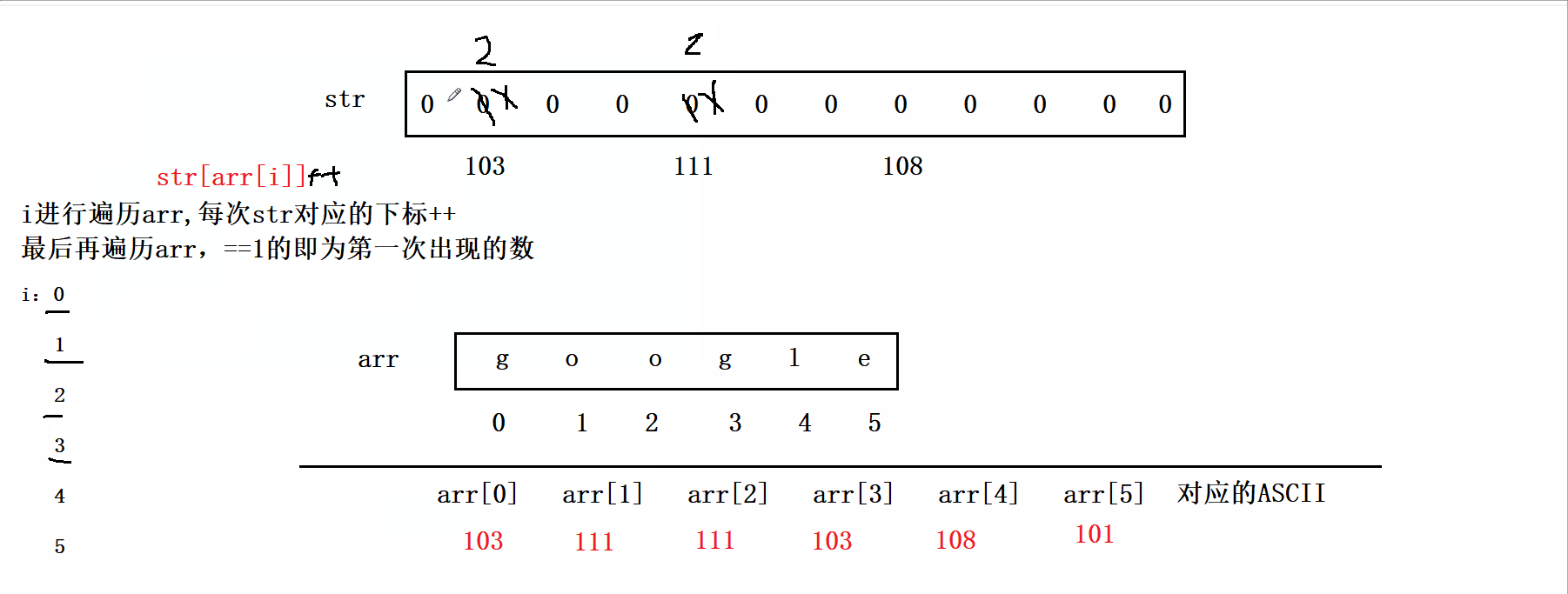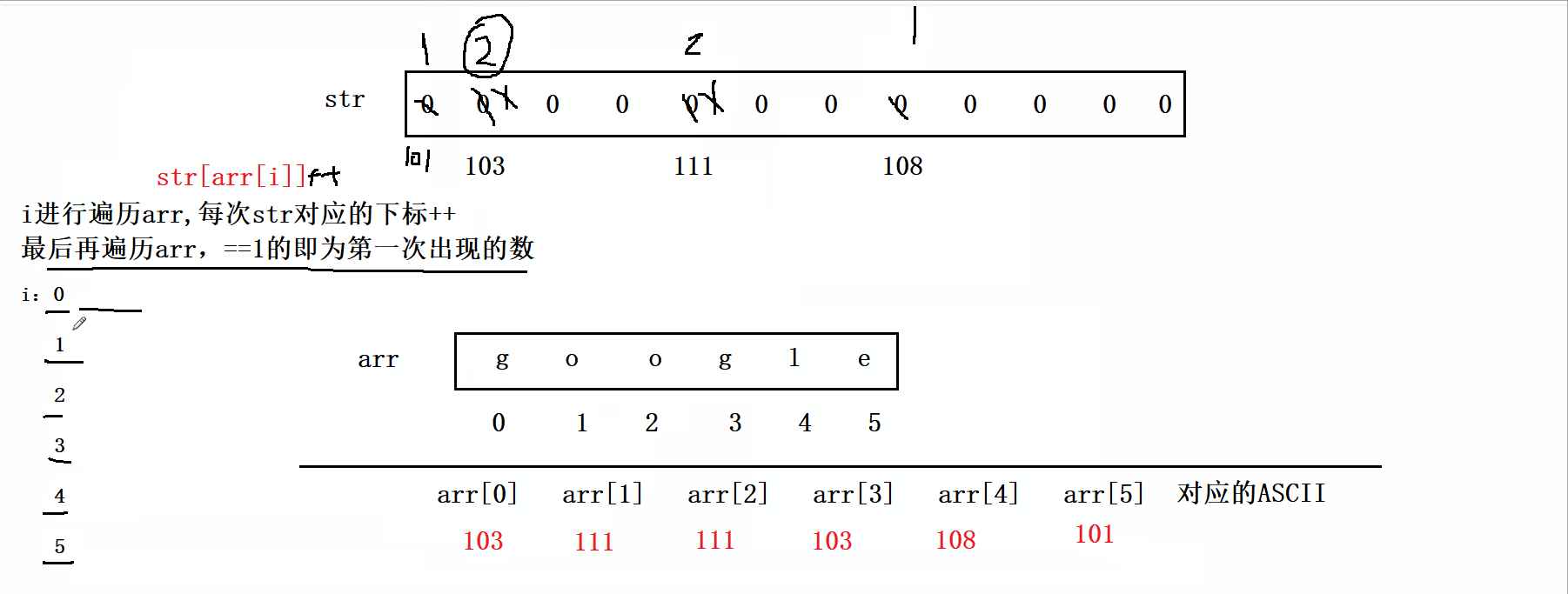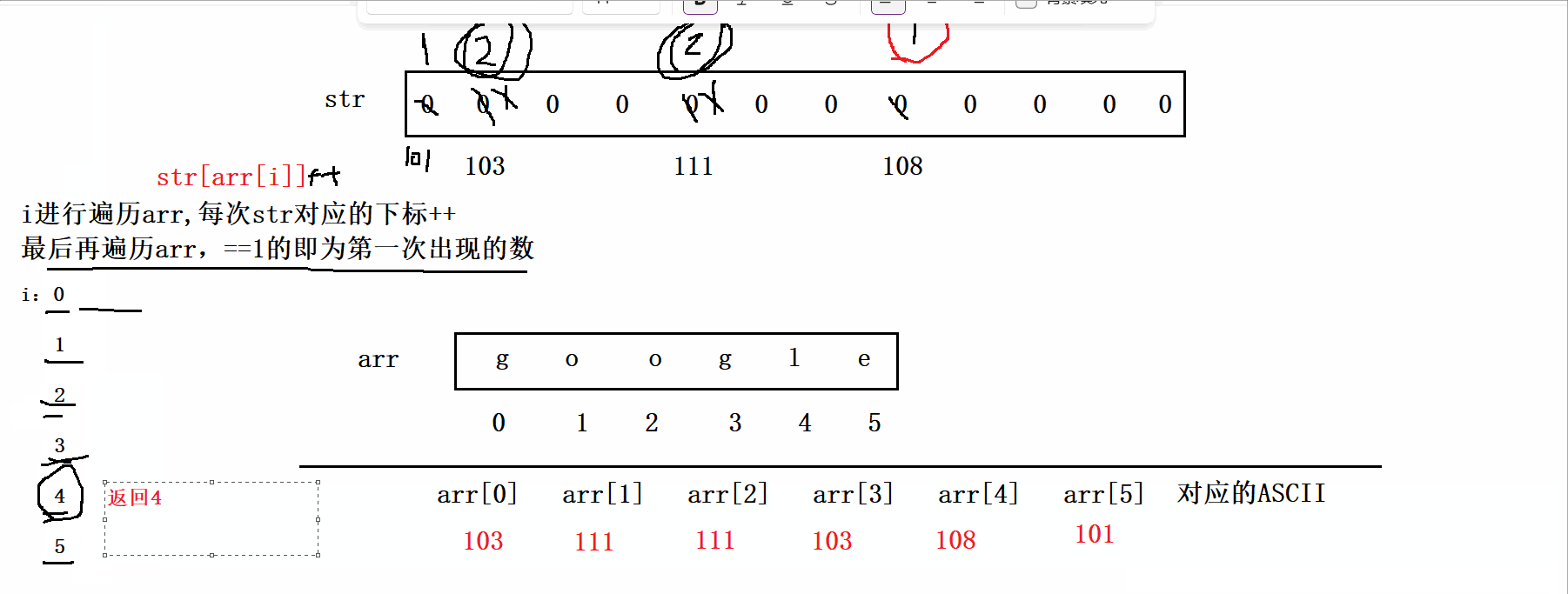
题目如下：

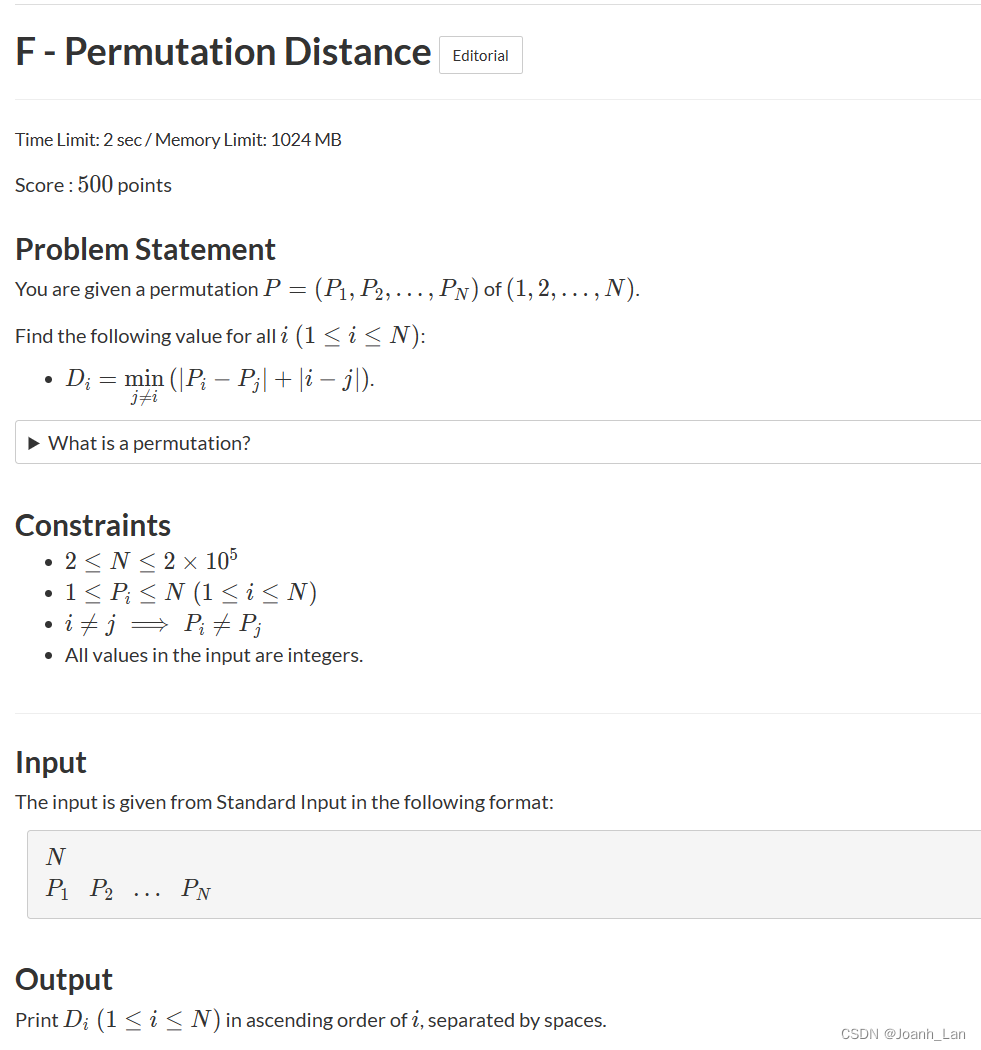
题目链接

题解 or 思路：

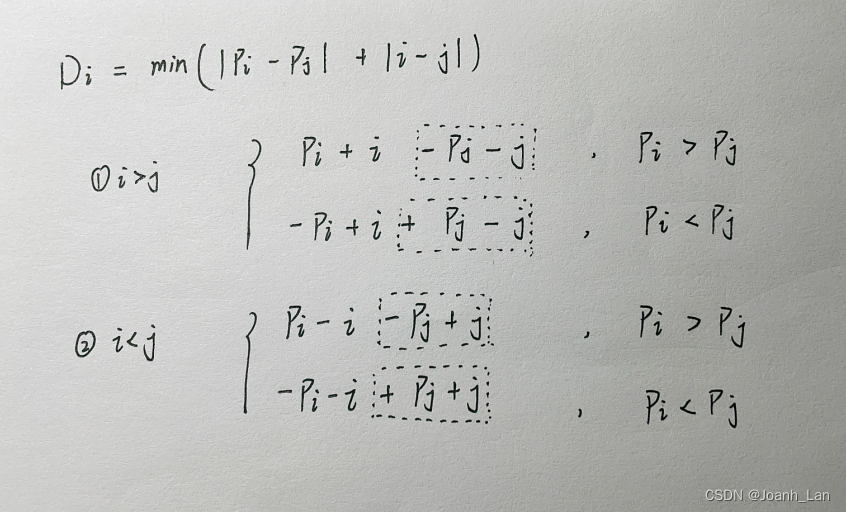
去掉绝对值后 有 $2\times 2=4$ 中情况
虚线括起来的是需要维护的，其他直接枚举就行!

对于 $p_i<p_j$ 的情况，设我们维护的式子为 $x$
那我们每次枚举查找的范围为 $[s[i],n]$
为了简便代码的书写，我们可以插入的时候 $s[i]$ 变成 $n-s[i]+1$,那么查找就变成 $[1,n-s[i]+1]$

可以结合下面代码进行理解

AC 代码如下：

#define int long long
const int N = 200009;
const int inf = 2147483647;
int n, s[N], res[N];
int lowbit(int x)
{
    return x & -x;
}
struct nn
{
    int tree[N];
    void update(int x, int d)
    {
        for (int i = x; i <= n; i += lowbit(i))
            tree[i] = min(tree[i], d);
    }
    int query(int x)
    {
        int ans = inf;
        for (int i = x; i; i -= lowbit(i))
            ans = min(ans, tree[i]);
        return ans;
    }
} lan[2];

void solve()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
        cin >> s[i];
    fill(lan[0].tree + 1, lan[0].tree + n + 1, inf);
    fill(lan[1].tree + 1, lan[1].tree + n + 1, inf);
    for (int i = 1; i <= n; i++)
    {
        res[i] = min(s[i] + i + lan[0].query(s[i]), i - s[i] + lan[1].query(n - s[i] + 1));
        lan[0].update(s[i], -s[i] - i);
        lan[1].update(n - s[i] + 1, s[i] - i);
    }
    fill(lan[0].tree + 1, lan[0].tree + n + 1, inf);
    fill(lan[1].tree + 1, lan[1].tree + n + 1, inf);
    for (int i = n; i >= 1; i--)
    {
        res[i] = min({res[i], s[i] - i + lan[0].query(s[i]), -s[i] - i + lan[1].query(n - s[i] + 1)});
        lan[0].update(s[i], i - s[i]);
        lan[1].update(n - s[i] + 1, s[i] + i);
    }
    for (int i = 1; i <= n; i++)
        cout << res[i] << " \n"[i == n];
}
signed main()
{
    buff;
    solve();
}