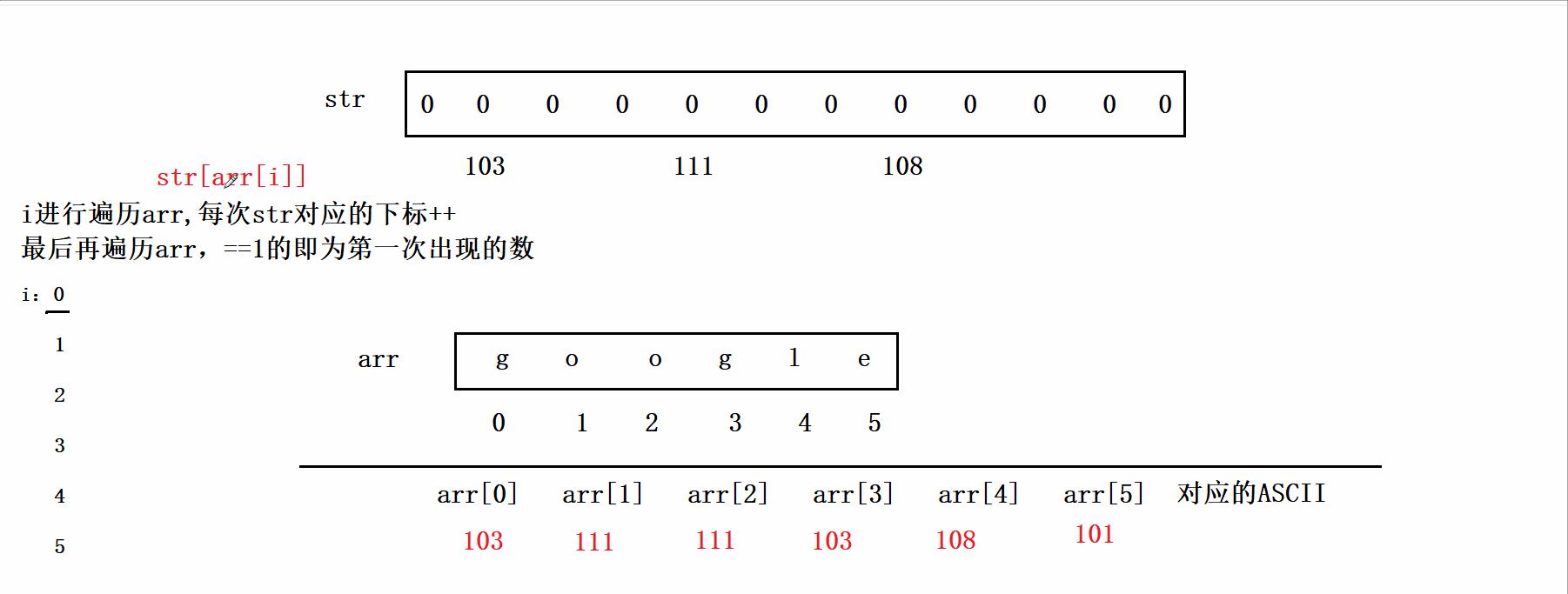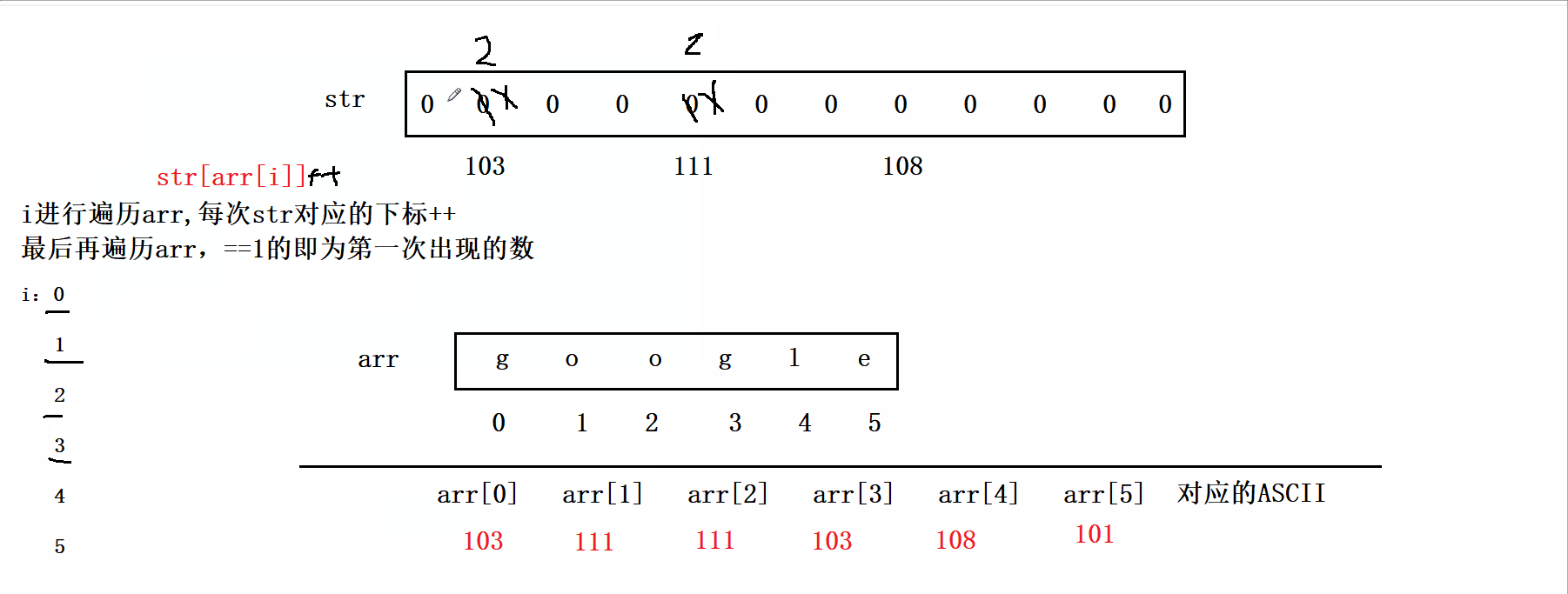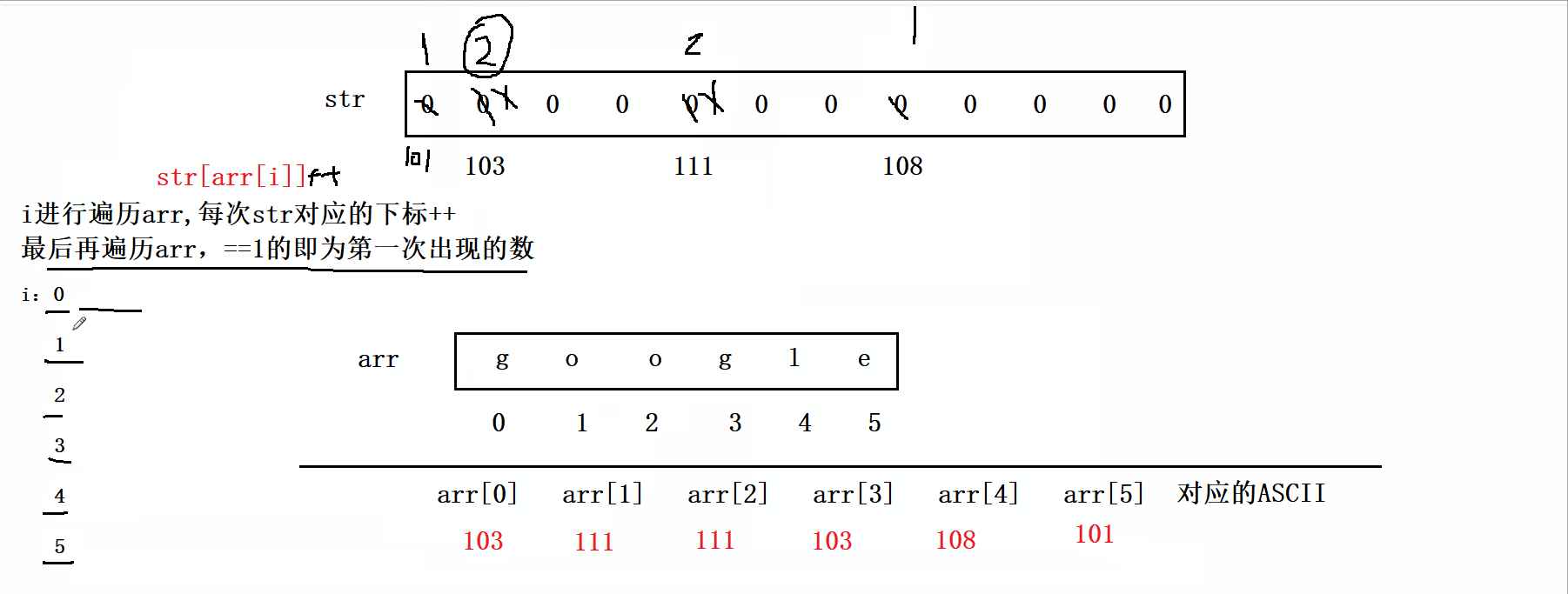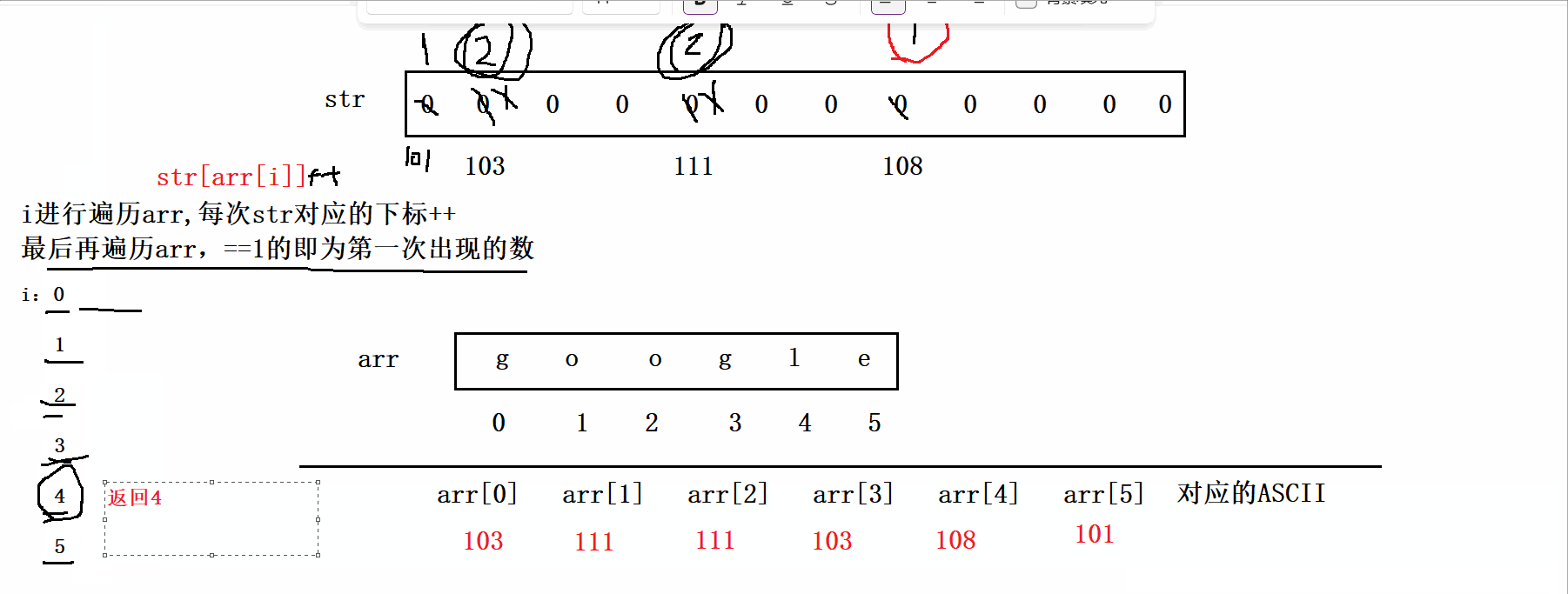
学习资料是Github的一个项目Tiny renderer or how OpenGL works: software rendering in 500 lines of code

本文对应原教程的第二课的部分内容

原教程重在思路，主要内容是以推导为主，所以这里还是记录思路和为代码做注释

知乎也有人给出了中译版：[从零构建光栅渲染器] 0.引言

三角形的线框绘制与区域填充

教程给出的代码中，geometry.h的引用处要加一行#include <ostream>，否则报错

最基础的方法固然是借用已经实现的画线函数line，对三个顶点两两一组依次使用即可，使用方法类似如下：

// defination
void triangle(Vec2i t0, Vec2i t1, Vec2i t2, TGAImage &image, TGAColor color) { 
    line(t0, t1, image, color); 
    line(t1, t2, image, color); 
    line(t2, t0, image, color); 
}

// ...

// using in code
Vec2i t0[3] = {Vec2i(10, 70),   Vec2i(50, 160),  Vec2i(70, 80)}; 
Vec2i t1[3] = {Vec2i(180, 50),  Vec2i(150, 1),   Vec2i(70, 180)}; 
Vec2i t2[3] = {Vec2i(180, 150), Vec2i(120, 160), Vec2i(130, 180)}; 
triangle(t0[0], t0[1], t0[2], image, red); 
triangle(t1[0], t1[1], t1[2], image, white); 
triangle(t2[0], t2[1], t2[2], image, green);

一个好的绘制三角形的方法应该有以下几个特点：

• 应该是简单和高效的
• 对称的，图片不应该取决于传递给绘制函数的顶点顺序

---

作者给出的方法是：

1. 按Y坐标对构成三角形的顶点进行排序
2. 对三角形的左右两边同时进行光栅化
3. 在左右两边之间的区域内使用水平线填充

这类似就是多边形区域填充中的扫描线方法

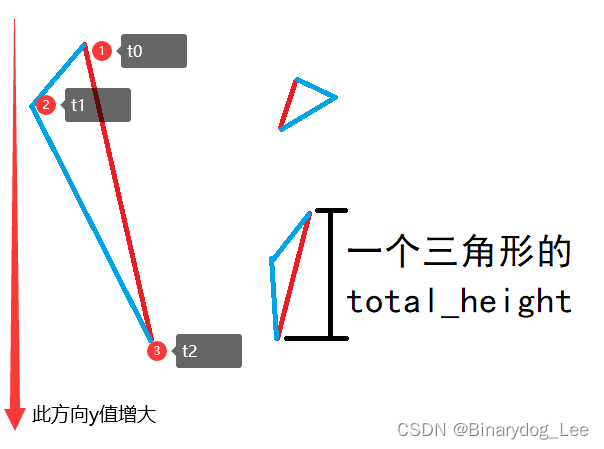
作者的意思是将一个三角形的边分为左右两部分来看，其中一个部分是y轴最下方的顶点到最上方的顶点的连线（红色部分，y方向跨度最大），其余的构成另一部分，这一部分拥有两条线段，显然不是一次就能绘制完的

void triangle(Vec2i t0, Vec2i t1, Vec2i t2, TGAImage &image, TGAColor color) { 
    // sort the vertices, t0, t1, t2 lower−to−upper (bubblesort yay!) 
    if (t0.y>t1.y) std::swap(t0, t1); 
    if (t0.y>t2.y) std::swap(t0, t2); 
    if (t1.y>t2.y) std::swap(t1, t2); 
    int total_height = t2.y-t0.y; 
    for (int y=t0.y; y<=t1.y; y++) { 
        int segment_height = t1.y-t0.y+1; 
        float alpha = (float)(y-t0.y)/total_height; 
        float beta  = (float)(y-t0.y)/segment_height; // be careful with divisions by zero 
        Vec2i A = t0 + (t2-t0)*alpha; 
        Vec2i B = t0 + (t1-t0)*beta; 
        if (A.x>B.x) std::swap(A, B); 
        for (int j=A.x; j<=B.x; j++) { 
            image.set(j, y, color); // attention, due to int casts t0.y+i != A.y 
        } 
    } 
    for (int y=t1.y; y<=t2.y; y++) { 
        int segment_height =  t2.y-t1.y+1; 
        float alpha = (float)(y-t0.y)/total_height; 
        float beta  = (float)(y-t1.y)/segment_height; // be careful with divisions by zero 
        Vec2i A = t0 + (t2-t0)*alpha; 
        Vec2i B = t1 + (t2-t1)*beta; 
        if (A.x>B.x) std::swap(A, B); 
        for (int j=A.x; j<=B.x; j++) { 
            image.set(j, y, color); // attention, due to int casts t0.y+i != A.y 
        } 
    } 
}

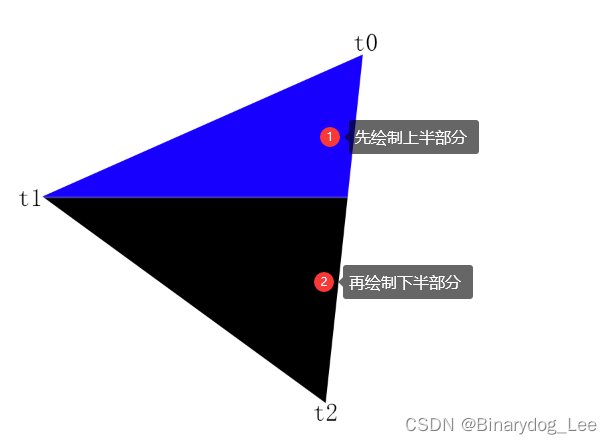
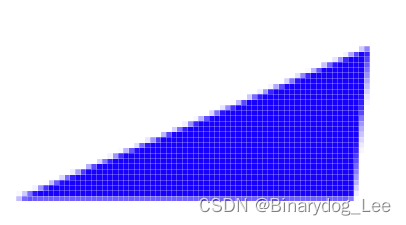
根据上面的代码，两个for循环分别绘制一个三角形的上半部分和下半部分。由于图形是像素组成的，这里要对每部分的像素按行绘制（就是上面作者提到的三点中的第三点），如下图可以所示（这个图是我在PS作的，有抗锯齿，但是这里绘制的不应该有抗锯齿）。外层for循环的每一次，就绘制好了一行，内存for循环一次，是绘制这一行的其中一个像素点。

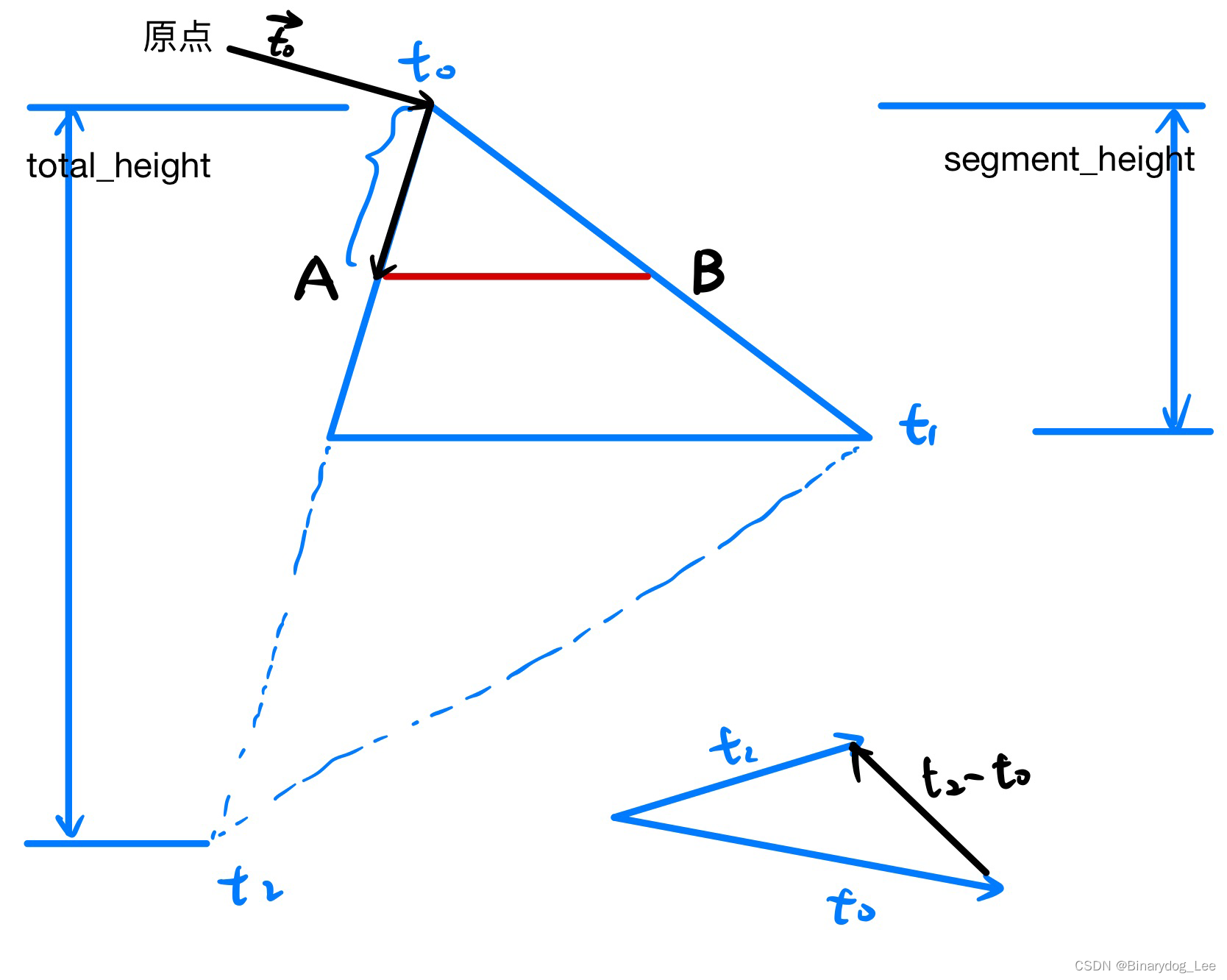
单拿出一个for循环看，其中外层循环先算出这条线的左右端点（即代码中的A和B），而这个左右端点的计算，要依靠aplha和beta这两个变量，而这两个变量，以上半部分为例，就是当前绘制横线（红色）的y坐标到底端（t0的y坐标）的差，占整个三角形y方向长度的比例，用这个就可以推知下图A这个向量（即原点指向A点的向量），即A = t0 + (t2-t0)*alpha，B向量同理。知道向量，自然就知道A点在哪，以及B点在哪。

按照比例（等比三角形），A、B点连线本身也是水平于坐标轴的，故而可以使用两点的X坐标作为两端，在它们中间填充像素

float alpha = (float)(y-t0.y)/total_height; 
float beta  = (float)(y-t0.y)/segment_height; // be careful with divisions by zero 

并且这个代码有两个问题，一个是重复代码过多，另一个是某些情况无法绘制（注释中说了，segment_height有可能为0，此时不能做除数），故而进行优化：

void triangle(Vec2i t0, Vec2i t1, Vec2i t2, TGAImage &image, TGAColor color) { 
    if (t0.y==t1.y && t0.y==t2.y) return; // I dont care about degenerate triangles 
    // sort the vertices, t0, t1, t2 lower−to−upper (bubblesort yay!) 
    if (t0.y>t1.y) std::swap(t0, t1); 
    if (t0.y>t2.y) std::swap(t0, t2); 
    if (t1.y>t2.y) std::swap(t1, t2); 
    int total_height = t2.y-t0.y; 
    for (int i=0; i<total_height; i++) { 
        bool second_half = i>t1.y-t0.y || t1.y==t0.y; 
        int segment_height = second_half ? t2.y-t1.y : t1.y-t0.y; 
        float alpha = (float)i/total_height; 
        float beta  = (float)(i-(second_half ? t1.y-t0.y : 0))/segment_height; // be careful: with above conditions no division by zero here 
        Vec2i A = t0 + (t2-t0)*alpha; 
        Vec2i B = second_half ? t1 + (t2-t1)*beta : t0 + (t1-t0)*beta; 
        if (A.x>B.x) std::swap(A, B); 
        for (int j=A.x; j<=B.x; j++) { 
            image.set(j, t0.y+i, color); // attention, due to int casts t0.y+i != A.y 
        } 
    } 
}

观察以上代码，可以发现的有

如果segment_height为0，则三角形有一条边本身就是平行于扫描线的方向，即X轴方向。此时本身相当于绘制上面例子中三角形的下半部分（即所谓的second_half）。

因此代码中设置了second_half变量，绘制下半部分有两种情况，一种是确实在绘制下半部分（即i>t1.y-t0.y），第二种是绘制上面说的底边平行于扫描线方向（即t1.y==t0.y），也当做绘制下半部分。

以second_half作为标志变量，有选择性地更改segment_height和beta，实现了在一个for写完所有操作。

这就是绘制2D三角形的方法了

题外话：重心坐标系

这是另一种绘制三角形的方法

作者随即提到了一个叫做重心坐标系（barycentric coordinates）的东西。我直接拿一张维基百科的图展示一下：

补充链接：计算机图形学三(补充)：重心坐标(barycentric coordinates)详解及其作用

不难发现该坐标系有3个维度，顶点处必有一个维度为1，其他为0。重心处是(1/3, 1/3, 1/3)。因此这是一种全新的思路：在重心坐标系检查某个坐标是否处于三角形内。

很简单，如果这个坐标的三个分量有负值，就说明在三角形外

Tips：某点若在三角形内部则其在该三角形的重心坐标系下三个分量都为非负数

因此我们需要一个barycentric()函数，它计算给定三角形中点 P 的坐标。

至于triangle()函数，它计算边界盒。定义一个边界盒需要知道左下角和右上角。为了找到这些位置，我们迭代了三角形的所有顶点并且找到最小/最大的坐标。我们会在边界盒的范围内，逐点检查它是否在三角形内。

#include <vector> 
#include <iostream> 
#include "geometry.h"
#include "tgaimage.h" 
 
const int width  = 200; 
const int height = 200; 
 
Vec3f barycentric(Vec2i *pts, Vec2i P) { 
    Vec3f u = Vec3f(pts[2][0]-pts[0][0], pts[1][0]-pts[0][0], pts[0][0]-P[0])^Vec3f(pts[2][1]-pts[0][1], pts[1][1]-pts[0][1], pts[0][1]-P[1]);
    /* `pts` and `P` has integer value as coordinates
       so `abs(u[2])` < 1 means `u[2]` is 0, that means
       triangle is degenerate, in this case return something with negative coordinates */
    if (std::abs(u.z)<1) return Vec3f(-1,1,1);
    return Vec3f(1.f-(u.x+u.y)/u.z, u.y/u.z, u.x/u.z); 
} 
 
void triangle(Vec2i *pts, TGAImage &image, TGAColor color) { 
    Vec2i bboxmin(image.get_width()-1,  image.get_height()-1); 
    Vec2i bboxmax(0, 0); 
    Vec2i clamp(image.get_width()-1, image.get_height()-1); 
    for (int i=0; i<3; i++) { 
        bboxmin.x = std::max(0, std::min(bboxmin.x, pts[i].x));
	bboxmin.y = std::max(0, std::min(bboxmin.y, pts[i].y));

	bboxmax.x = std::min(clamp.x, std::max(bboxmax.x, pts[i].x));
	bboxmax.y = std::min(clamp.y, std::max(bboxmax.y, pts[i].y));
    } 
    Vec2i P; 
    for (P.x=bboxmin.x; P.x<=bboxmax.x; P.x++) { 
        for (P.y=bboxmin.y; P.y<=bboxmax.y; P.y++) { 
            Vec3f bc_screen  = barycentric(pts, P); 
            if (bc_screen.x<0 || bc_screen.y<0 || bc_screen.z<0) continue; 
            image.set(P.x, P.y, color); 
        } 
    } 
} 
 
int main(int argc, char** argv) { 
    TGAImage frame(200, 200, TGAImage::RGB); 
    Vec2i pts[3] = {Vec2i(10,10), Vec2i(100, 30), Vec2i(190, 160)}; 
    triangle(pts, frame, TGAColor(255, 0, 0)); 
    frame.flip_vertically(); // to place the origin in the bottom left corner of the image 
    frame.write_tga_file("framebuffer.tga");
    return 0; 
}

阅读完代码，就得去理解Vec3f barycentric(Vec2i*, Vec2i)这个函数的原理，关键之处就是下面的这行代码：

Vec3f u = Vec3f(pts[2][0]-pts[0][0], pts[1][0]-pts[0][0], pts[0][0]-P[0])^Vec3f(pts[2][1]-pts[0][1], pts[1][1]-pts[0][1], pts[0][1]-P[1]);

能够看到在triangle函数中调用了这个函数，调用的思路是对于边界盒内的每个点P，依次调用Vec3f bc_screen = barycentric(pts, P); ，检查返回的重心坐标系下的坐标点bc_screen，若某分量小于0则不做任何事情，若均不小于0，则认为在三角形内，进行指定操作（在这里则是绘制）。

其中需要知道的是pts是什么，从main函数处的调用可以知道它是三角形的三个点的坐标，类型是Vec2i[3]（我知道可能在C++中这么说不严谨），即每个点是一个Vec2i类型变量。

能猜出来这个代码是将笛卡尔坐标系转化为重心坐标系的，但是实现$(x,y)$到$(\alpha ,\beta ,\gamma )$的转换的公式是什么？可以从上面的链接文章和后面这个链接里找到：重心坐标系

我直接拿上面链接的知乎中译版截个图：

到这里最后一个式子就是要解的，实际上是要$(u,v,1)$与$(A{B}_x,A{C}_x,P{A}_x)$及$(A{B}_y,A{C}_y,P{A}_y)$这两个向量正交（点积为零）

正交的定义：对于向量$\alpha$和$\beta$，有$(\alpha ,\beta )={\alpha }^T\beta =0$

对于点积$\alpha ⸳\beta$的几何意义是$\alpha$在$\beta$上的投影，点积为零意味着垂直或者说正交。点积忘了的可以看：向量点乘与叉乘的概念及几何意义

点积的公式是$\alpha ⸳\beta =|\alpha ||\beta |cos\theta$

那么与这两个向量都垂直的向量$(u,v,1)$，可以用叉乘得到该变量的方向，之后再修改一下长度就好了。叉乘的性质就是对于不同向的两个向量$\alpha$和$\beta$，叉乘$\alpha \times \beta$得到的结果是个向量，且同时垂直于$\alpha$和$\beta$这两个向量。

总归这个原理是弄明白了，但是问题是为什么Vec3f的构造函数接受这么多参数，是我没想明白的。

此外就是代码中的Vec3f的^运算，实际上就是叉乘，可以在给的头文件里面找到定义：

inline Vec3<t> operator ^(const Vec3<t> &v) const { return Vec3<t>(y*v.z-z*v.y, z*v.x-x*v.z, x*v.y-y*v.x); }