（1）ACWing 1015. 摘花生 1015. 摘花生 - AcWing题库
Hello Kitty想摘点花生送给她喜欢的米老鼠。她来到一片有网格状道路的矩形花生地(如下图)，从西北角进去，东南角出来。地里每个道路的交叉点上都有种着一株花生苗，上面有若干颗花生，经过一株花生苗就能摘走该它上面所有的花生。Hello Kitty只能向东或向南走，不能向西或向北走。问Hello Kitty最多能够摘到多少颗花生。
输入样例：
2
2 2
1 1
3 4
2 3
2 3 4
1 6 5输出样例：
8
16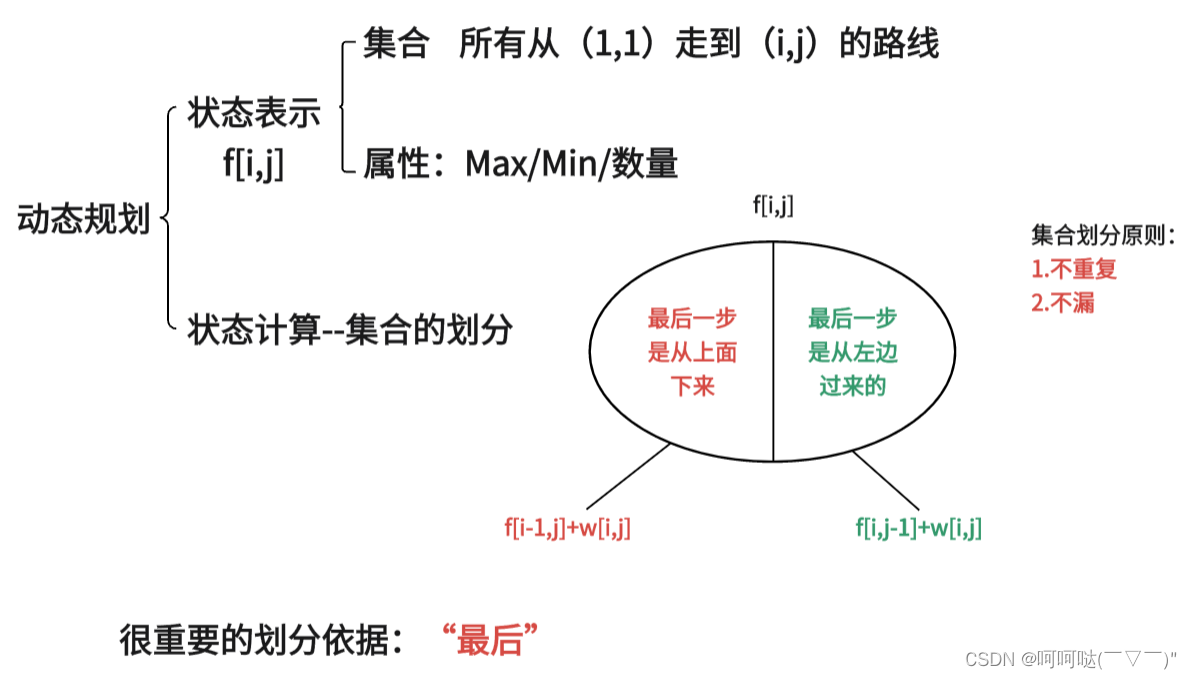
>>动规五部曲：
1.确定dp数组以及下标的含义
- dp[i][j] :为到达 (i , j) 位置的最多能够摘到的花生数，最终所求结果即为 dp[n][m]
2.确定递推公式
- dp[i][j] = max(dp [i][j − 1], dp[i − 1][j]) + w [i][j]
3.dp 数组初始化
- dp[i][j]初始化为0
4.确定遍历顺序
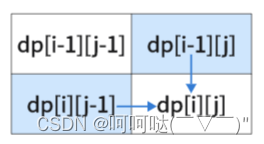
- 从上到下，从左到右遍历，这样能保证dp[i][j]是经过计算得来的
5.举例推导dp数组
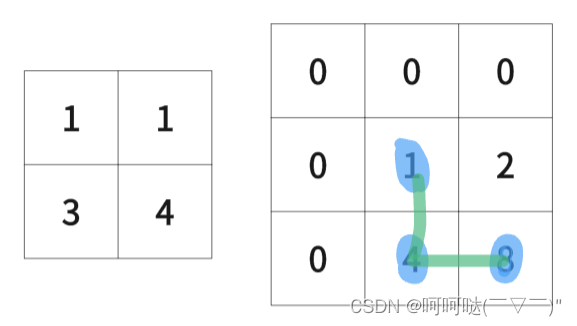
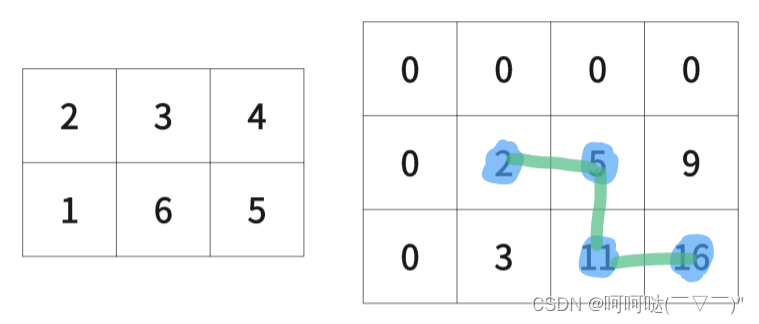
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m;
int w[N][N], dp[N][N];
int main() {
int T;
cin >> T;
while (T--) {
cin >> n >> m;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
cin >> w[i][j];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + w[i][j];
cout << dp[n][m] << endl;
}
}（2）ACWing 1018. 最低通行费(DP)
ACWing 1018. 最低通行费（原题链接）
题目描述：一个商人穿过一个 N × N 的正方形的网格，去参加一个非常重要的商务活动。他要从网格的左上角进，右下角出。每穿越中间 1 个小方格，都要花费 1 个单位时间。商人必须在 ( 2 N − 1 ) 个单位时间穿越出去。而在经过中间的每个小方格时，都需要缴纳一定的费用。这个商人期望在规定时间内用最少费用穿越出去。请问至少需要多少费用？
注意：不能对角穿越各个小方格（即，只能向上下左右四个方向移动且不能离开网格）
输入格式：第一行是一个整数，表示正方形的宽度 N。后面 N 行，
每行 N 个不大于 100 的正整数，为网格上每个小方格的费用
输出格式：输出一个整数，表示至少需要的费用
数据范围：1 ≤ N ≤ 100
输入样例：
5
1 4 6 8 10
2 5 7 15 17
6 8 9 18 20
10 11 12 19 21
20 23 25 29 33输出样例：
109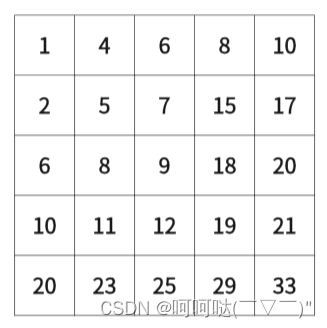 
关键信息：时间不超过 (2 N − 1) ，意味着不能走回头路！！！
发现不能走回头路的性质后就和 ACWing 1015.摘花生 基本一样了，只不过将最大值换成了最小值
>>动规五部曲：
1.确定dp数组以及下标的含义
- dp[i][j] :为到达 (i , j) 位置的最小通行费，最终所求结果即为 dp[n][n]
2.确定递推公式
- dp[i][j] = min (dp[i][j − 1], dp[i − 1][j]) + w [i][j]
3.dp 数组初始化
- dp[i][j]初始化为INF
- dp[0][1]=0;dp[1][0]=0
4.确定遍历顺序
- 从上到下，从左到右遍历，这样能保证dp[i][j]是经过计算得来的
5.举例推导dp数组
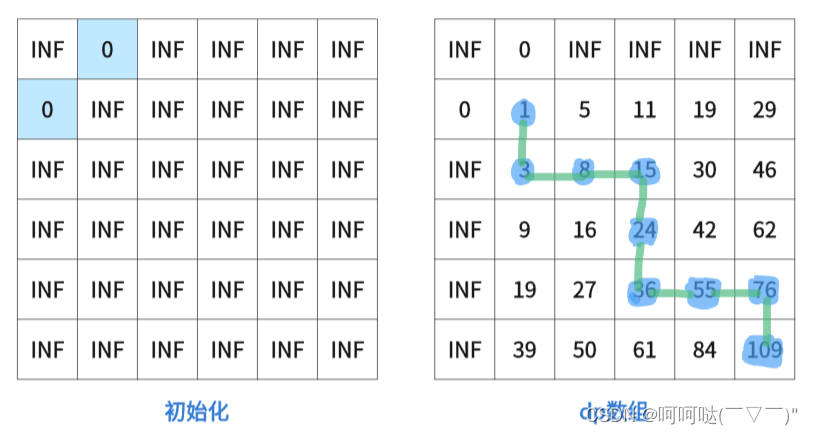
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110,INF = 1e9;
int n;
int w[N][N];
int dp[N][N];
int main() {
scanf_s("%d", &n);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
scanf_s("%d", &w[i][j]);
memset(dp, 0x3f, sizeof dp);
dp[0][1] = 0; dp[1][0] = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + w[i][j];
}
printf("%d\n", dp[n][n]);
return 0;
}>>知识点回顾：
（1）最常用的memset赋值
#include <cstring>
memset(f, 0, sizeof(f));
0x3f(正无穷)
-0x3f(负无穷)
memset(f, 0x3f, sizeof(f)); 每个元素大小1,061,109,567
memset(f, -0x3f, sizeof(f)); 每个元素大小-1,044,266,559推荐和参考文章：
普通数组的memset函数用法详细解读_memset数组-CSDN博客
https://blog.csdn.net/qq_43827595/article/details/101452656ACWing 1018. 最低通行费(DP)-CSDN博客https://blog.csdn.net/zzcstxwd/article/details/127530180（3）ACWing 1027.方格取数
https://www.acwing.com/problem/content/1027/
设有 NxN 的方格图，我们在其中的某些方格中填入正整数，而其他的方格中则放入数字0，如下图所示：
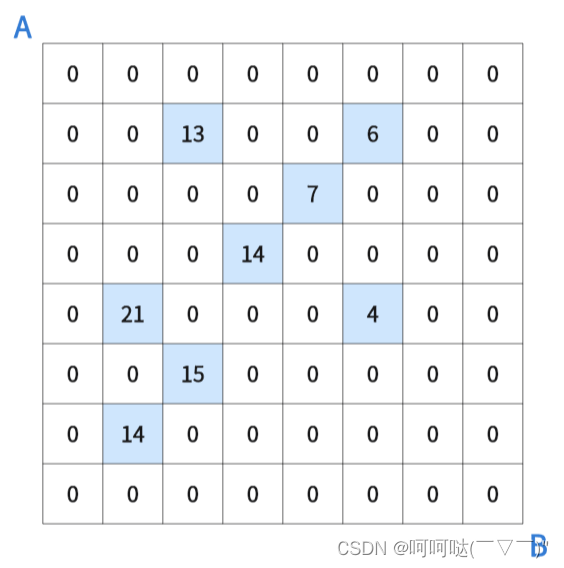
某人从图中的左上角A出发，可以向下行走，也可以向右行走，直到到达右下角的B点。在走过的路上，他可以取走方格中的数（取走后的方格中奖变为数字0）。此人从A点到B点共走了两次，试找出两条这样的路径，使得取得的数字和为最大。
输入格式：第一行为一个整数N，表示 NxN 的方格图。接下来的每行有三个整数，
第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数，
一行"0 0 0"表示结束
输出格式：输出一个整数，表示两条路径上取得的最大的和
数据范围：N<=10
输入样例:
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0输出样例:
67>>思考只走一次和走两次：
只走一次：f[i,j] 表示所有从（1,1）走到（i,j）的路径的最大值
- f[i,j] = max(f[i-1,j]+w[i,j],f[i,j-1]+w[i,j])
走两次：f[i1,j1,i2,j2] 表示所有从（1,1）,（1,1）分别走到（i1,j1）,（i2,j2）的路径的最大值。考虑一下两条路线什么时候会走到同一个格子呢？
这个题有两种思路：
- 第一种思路：第一个人先走，然后标记一下，接着第二个人再走
- 第二种思路：同时走
同时走的话，如何处理“同一个格子不能被重复选择”?
需要考虑的是什么时候两条路线会有交集呢？必然在同一个格子的时候会有交集。那它们走到同一个格子的时候，这两条路线走过的总步数是一样的。
- i1+j1==i2+j2 时,两条路径的格子才可能重合
其中k：k = i1+j1= i2+j2（k表示两条路线当前走到的格子的横纵坐标之和）
- f[k,i1,i2] 表示所有从（1,1）,（1,1）分别走到（i1,k-i1）,（i2,k-i2）的路径的最大值
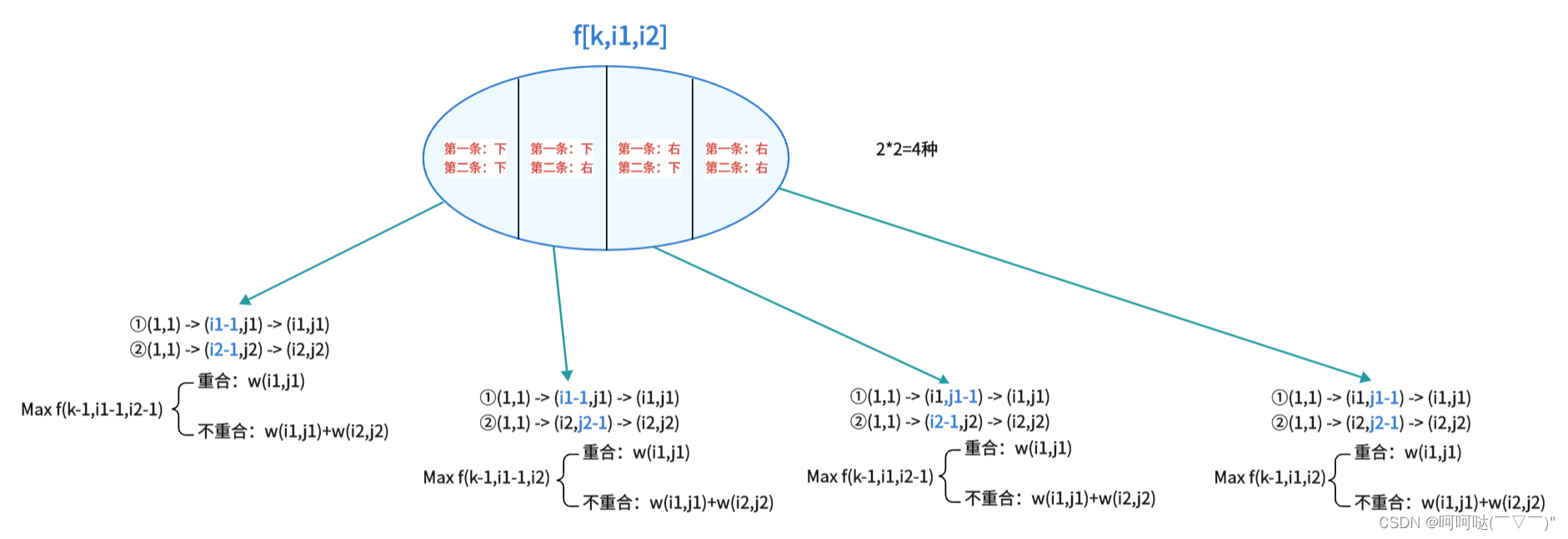
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 15;
int n;
int w[N][N];
int f[N*2][N][N];
int main() {
scanf_s("%d", &n);
int a, b, c;
while (cin >> a >> b >> c, a || b || c) w[a][b] = c;
for(int k=2;k<=n+n;k++)
for (int i1 = 1; i1 <= n; i1++)
for (int i2 = 1; i2 <= n; i2++) {
int j1 = k - i1, j2 = k - i2;
if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n) {
int t = w[i1][j1];
if (i1 != i2) t += w[i2][j2];
int& x = f[k][i1][i2];
x = max(x, f[k - 1][i1 - 1][i2 - 1] + t);
x = max(x, f[k - 1][i1 - 1][i2] + t);
x = max(x, f[k - 1][i1][i2 - 1] + t);
x = max(x, f[k - 1][i1][i2] + t);
}
}
printf("%d\n", f[n + n][n][n]);
return 0;
}知识回顾：“p->q”：① q是p的必要条件; ② p是q的充分条件
![[UDS] --- DiagnosticSessionControl 0x10 service](https://img-blog.csdnimg.cn/e8b70ca29e14402eacda142f246961e2.png)
