目录

一，题目

二，题目接口

 三，解题思路及其代码

---

一，题目

在一条环路上有 n 个加油站，其中第 i 个加油站有汽油 gas[i] 升。

你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

给定两个整数数组 gas 和 cost ，如果你可以按顺序绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1 。如果存在解，则 保证 它是 唯一 的。

二，题目接口

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        

    }
};

 三，解题思路及其代码

1.暴力解法

   其实对于这道题很容易想到的便是一个暴力解法，这个暴力解法的大概思路便是对每一个下标下进行试验，如果我的这个下标在经过一圈之后能回到我原来的下标的话，那么我这个下标便是能够符合条件的。

 如何找到符合条件的下标呢？

1.若该下标的rest+gas[i]-cost[i]是整数那我便可以到达下一个加油站。

2.为了防止我的下标越界，必须有%n的操作（n是数组的长度）。

代码：

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
               int n = gas.size();//计算长度
              int startPos = 0;//从零开始出发
              
             for(int i = 0;i<n;i++)//遍历找正确的加油站
             {
                  startPos = i;
                  int rest = 0;//记录车箱里剩余的油

                  while(gas[startPos%n]+rest>=cost[startPos%n]&&startPos<2*n)//若符合条件便可到达下一个加油站
                  {
                      rest = gas[startPos%n] - cost[startPos%n]+rest;//记录剩余的油
                      startPos++;
                      int pos =  startPos%n;
                      if(pos == i)//判断是否回到出发时的加油站处
                      {
                        return i;//回到了便可以返回这个加油站的下标
                      }
                  }

             }

             return -1;//没有这样的加油站便返回-1

    }
};

对于暴力解法，肯定是会超时的：

所以我们就得开始写一个贪心的解法。

2.贪心解法：

如何实现贪心呢？先来举个例子：

比如我的gas = [5,1,2,3,4],cost = [4,4,1,5,1]

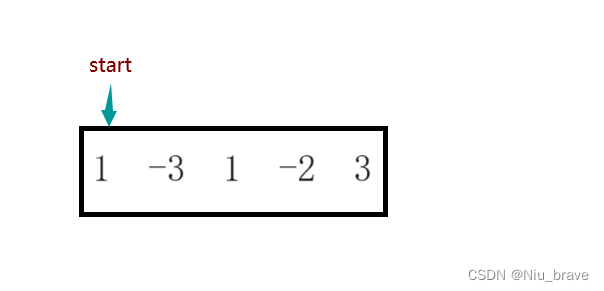
我们可以先来计算一下这两个数组之间的差用一个diff数组记录下来：diff = [1,-3,1,-2,3]

首先我们先以第一个1位起点：

因为我们的1是一个正数，所以我可以往后走。但是在遇到-3时我的1+（-3）为负数，所以我就不能再往下走了，这时贪心的地方便来了，我就得从-3的下一位开始走了。

仿照这个思路改造一份贪心代码，并注意越界问题，代码如下：

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
              int n = gas.size();
              int rest = 0;
              
             for(int i = 0;i<n;i++)
             {
                  int rest = 0;
                  int step = 0;
                  for( ;step<n;step++)
                  {
                      rest = rest+gas[(i+step)%n]-cost[(i+step)%n];
                      if(rest<0)
                      {
                        break;
                      }
                  }

                 if(rest>=0)
                 {
                   return i;
                 }

                  i+=step;//加step步，再加上for里面的++便是增加step+1步！！！
             }

             return -1;

    }
};

过啦：