文章目录
- abstract
- 第一类换元法
- 第二类换元法
- 分析
- 定理👺
- 证明
- 第二类换元公式的应用
- 倒代换
- 三角恒等化去根式
- 其他使用第二换元法情形
- 例
- 附加积分公式表
- 例
- 附
abstract
- 第二类换元法(简称第二换元法)的原理和应用
第一类换元法
- 通过变量代换 u = ϕ ( x ) u=\phi(x) u=ϕ(x), ∫ f ( ϕ ( x ) ) ϕ ′ ( x ) d x \int{f(\phi(x))\phi'(x)}\mathrm{d}x ∫f(ϕ(x))ϕ′(x)dx= ∫ f ( u ) d u \int{f(u)\mathrm{d{u}}} ∫f(u)du,这类换元法的运用比较注重被积函数的形式变形和凑微分的能力,某些时候难以达成应用此类换元法的条件
第二类换元法
分析
- 通过变量代换
x
=
ϕ
(
t
)
x=\phi(t)
x=ϕ(t),则
∫
f
(
x
)
d
x
\int{f(x)\mathrm{d}x}
∫f(x)dx=
∫
f
(
ϕ
(
t
)
)
ϕ
′
(
t
)
d
t
\int{f(\phi(t))}\phi'(t)\mathrm{d}t
∫f(ϕ(t))ϕ′(t)dt
(0) - 条件:
- 等式右边的不定积分存在(即 f ( ϕ ( t ) ) ϕ ′ ( t ) f(\phi(t))\phi'(t) f(ϕ(t))ϕ′(t)存在原函数)
- 设积分变量为
t
t
t积分后的结果为
T
(
t
)
T(t)
T(t),需要回代
x
=
ϕ
(
t
)
x=\phi(t)
x=ϕ(t)的反函数
t
=
ϕ
−
1
(
x
)
t=\phi^{-1}(x)
t=ϕ−1(x),得到关于变量
x
x
x的结果
- 为了保证反函数存在且可导,这里假定:直接函数 x = ϕ ( t ) x=\phi(t) x=ϕ(t)在某个区间 D ϕ D_{\phi} Dϕ上是单调可导的,且 ϕ ′ ( t ) ≠ 0 \phi'(t)\neq{0} ϕ′(t)=0
- 这里 D ϕ D_{\phi} Dϕ区间和 D f D_{f} Df区间通过 x = ϕ ( t ) x=\phi(t) x=ϕ(t)相对应
定理👺
-
归纳成定理:设 x = ϕ ( t ) x=\phi(t) x=ϕ(t)是单调可导函数,并且 ϕ ′ ( t ) ≠ 0 \phi'(t)\neq{0} ϕ′(t)=0( ϕ ( t ) \phi(t) ϕ(t)不是常数),又设 f ( ϕ ( t ) ) ϕ ′ ( t ) f(\phi(t))\phi'(t) f(ϕ(t))ϕ′(t)具有原函数(可积),则有换元公式: ∫ f ( x ) d x \int{f(x)\mathrm{d}x} ∫f(x)dx= [ ∫ f ( ϕ ( t ) ) ϕ ′ ( t ) d t ] t = ϕ − 1 ( x ) [\int{f(\phi(t))}\phi'(t)\mathrm{d}t]_{t=\phi^{-1}(x)} [∫f(ϕ(t))ϕ′(t)dt]t=ϕ−1(x)
(0-1)- 其中 t = ϕ − 1 ( x ) t=\phi^{-1}(x) t=ϕ−1(x)是 x = ϕ ( t ) x=\phi(t) x=ϕ(t)的反函数
证明
- 延续定理中的符号和条件说明进行证明
- 设
f
(
ϕ
(
t
)
)
ϕ
′
(
t
)
f(\phi(t))\phi'(t)
f(ϕ(t))ϕ′(t)的原函数为
Φ
(
t
)
\Phi(t)
Φ(t),(即
∫
f
(
ϕ
(
t
)
)
ϕ
′
(
t
)
d
t
\int{f(\phi(t))\phi'(t)}\mathrm{d}t
∫f(ϕ(t))ϕ′(t)dt=
Φ
(
t
)
+
C
\Phi(t)+C
Φ(t)+C)
- 为了便于叙述,记
Φ
(
t
)
\Phi(t)
Φ(t)=
Φ
(
ϕ
−
1
(
x
)
)
\Phi(\phi^{-1}(x))
Φ(ϕ−1(x))=
F
(
x
)
F(x)
F(x)
(1) - 只需要证明 F ( x ) F(x) F(x)是 f ( x ) f(x) f(x)的原函数,也就证明了 Φ ( t ) \Phi(t) Φ(t)是 f ( x ) f(x) f(x)的原函数
- 为了便于叙述,记
Φ
(
t
)
\Phi(t)
Φ(t)=
Φ
(
ϕ
−
1
(
x
)
)
\Phi(\phi^{-1}(x))
Φ(ϕ−1(x))=
F
(
x
)
F(x)
F(x)
- 由复合函数及反函数求导法则,对(1)两边关于
x
x
x求导
- 左边: d Φ d t ⋅ d t d x \frac{\mathrm{d}\Phi}{\mathrm{d}t}\cdot{\frac{\mathrm{d}t}{\mathrm{d}x}} dtdΦ⋅dxdt= f ( ϕ ( t ) ) ϕ ′ ( t ) ⋅ 1 ϕ ′ ( t ) f(\phi(t))\phi'(t)\cdot{\frac{1}{\phi'(t)}} f(ϕ(t))ϕ′(t)⋅ϕ′(t)1= f ( ϕ ( t ) ) f(\phi(t)) f(ϕ(t))= f ( x ) f(x) f(x)
- 右边: F ′ ( x ) F'(x) F′(x)
- 从而 F ′ ( x ) = f ( x ) F'(x)=f(x) F′(x)=f(x),说明 F ( x ) F(x) F(x)是 f ( x ) f(x) f(x)的一个原函数,即 ∫ f ( x ) d x \int{f(x)\mathrm{d}x} ∫f(x)dx= F ( x ) + C F(x)+C F(x)+C= Φ ( ϕ − 1 ( x ) ) + C \Phi(\phi^{-1}(x))+C Φ(ϕ−1(x))+C= Φ ( t ) + C \Phi(t)+C Φ(t)+C= [ ∫ f ( ϕ ( t ) ) ϕ ′ ( t ) d t ] t = ϕ − 1 ( x ) [\int{f(\phi(t))}\phi'(t)\mathrm{d}t]_{t=\phi^{-1}(x)} [∫f(ϕ(t))ϕ′(t)dt]t=ϕ−1(x)
第二类换元公式的应用
-
实际应用中,合适的代换 x = ϕ ( t ) x=\phi(t) x=ϕ(t)可能不容易看出
- 往往 x = ϕ ( t ) x=\phi(t) x=ϕ(t)的反函数 t = ψ ( x ) = ϕ − 1 ( x ) t=\psi(x)=\phi^{-1}(x) t=ψ(x)=ϕ−1(x)是容易建立的
- 再从 t = ψ ( x ) = ϕ − 1 ( x ) t=\psi(x)=\phi^{-1}(x) t=ψ(x)=ϕ−1(x)计算反函数得: x = ϕ ( t ) x=\phi(t) x=ϕ(t)
-
第二换元法比较适用于难以凑微分(第一换元法难以应用)的情况下,比如和基本积分表中相差较远的根式函数
倒代换
- 消去被积函数的分母中的变量因子 x x x
-
∫
a
2
−
x
2
x
4
d
x
\int{\frac{\sqrt{a^2-x^2}}{x^4}}\mathrm{d}x
∫x4a2−x2dx,
(
a
≠
0
)
(a\neq{0})
(a=0)
- 令 x = t − 1 x=t^{-1} x=t−1,则 d x \mathrm{d}x dx= − t − 2 d t -t^{-2}\mathrm{d}t −t−2dt
-
∫
a
2
−
x
2
x
4
d
x
\int{\frac{\sqrt{a^2-x^2}}{x^4}}\mathrm{d}x
∫x4a2−x2dx=
∫
a
2
−
t
−
2
t
−
4
(
−
t
−
2
)
d
t
\int{\frac{\sqrt{a^2-t^{-2}}}{t^{-4}}}(-t^{-2})\mathrm{d}t
∫t−4a2−t−2(−t−2)dt
- = − ∫ a 2 − t − 2 t − 2 d t -\int{\frac{\sqrt{a^2-t^{-2}}}{t^{-2}}}\mathrm{d}t −∫t−2a2−t−2dt= − ∫ ( a 2 − t − 2 ) t 4 d t -\int{\sqrt{(a^2-t^{-2})t^{4}}}\mathrm{d}t −∫(a2−t−2)t4dt= − ∫ a 2 t 4 − t 2 d t -\int{\sqrt{a^2t^4-t^2}}\mathrm{d}t −∫a2t4−t2dt= − ∫ ∣ t ∣ a 2 t 2 − 1 d t -\int{|t|\sqrt{a^2t^2-1}}\mathrm{d}t −∫∣t∣a2t2−1dt
- 当
x
>
0
x>0
x>0,即
t
>
0
t>0
t>0时,有
-
−
∫
∣
t
∣
a
2
t
2
−
1
d
t
-\int{|t|\sqrt{a^2t^2-1}}\mathrm{d}t
−∫∣t∣a2t2−1dt=
−
∫
(
a
2
t
2
−
1
)
1
/
2
t
d
t
-\int{({a^2t^2-1})^{1/2}}t\mathrm{d}t
−∫(a2t2−1)1/2tdt
- = − 1 2 ∫ ( a 2 t 2 − 1 ) 1 / 2 d t 2 -\frac{1}{2}\int{({a^2t^2-1})^{1/2}}\mathrm{d}t^2 −21∫(a2t2−1)1/2dt2= − 1 2 a 2 ∫ ( a 2 t 2 − 1 ) 1 / 2 d ( a 2 t 2 − 1 ) -\frac{1}{2a^2}\int{({a^2t^2-1})^{1/2}}\mathrm{d}(a^2t^2-1) −2a21∫(a2t2−1)1/2d(a2t2−1)= − 1 2 a 2 ⋅ 2 3 ( a 2 t 2 − 1 ) 3 2 + C -\frac{1}{2a^2}\cdot{\frac{2}{3}(a^2t^2-1)^\frac{3}{2}}+C −2a21⋅32(a2t2−1)23+C
- = − 1 3 a 2 ( ( a 2 t 2 − 1 ) 3 2 ) + C -\frac{1}{3a^2}({(a^2t^2-1)^\frac{3}{2}})+C −3a21((a2t2−1)23)+C= − 1 3 a 2 ( ( a 2 x − 2 − 1 ) 3 2 ) + C -\frac{1}{3a^2}({(a^2x^{-2}-1)^\frac{3}{2}})+C −3a21((a2x−2−1)23)+C
- = − 1 3 a 2 ( a 2 − x 2 x 2 ) 3 2 + C -\frac{1}{3a^2}(\frac{a^2-x^2}{x^{2}})^\frac{3}{2}+C −3a21(x2a2−x2)23+C= − 1 3 a 2 x 3 ( a 2 − x 2 ) 3 2 + C -\frac{1}{3a^2{x^{3}}}({a^2-x^2})^{\frac{3}{2}}+C −3a2x31(a2−x2)23+C
-
−
∫
∣
t
∣
a
2
t
2
−
1
d
t
-\int{|t|\sqrt{a^2t^2-1}}\mathrm{d}t
−∫∣t∣a2t2−1dt=
−
∫
(
a
2
t
2
−
1
)
1
/
2
t
d
t
-\int{({a^2t^2-1})^{1/2}}t\mathrm{d}t
−∫(a2t2−1)1/2tdt
三角恒等化去根式
- 经典根式积分@三角恒等去根式
其他使用第二换元法情形
例
-
∫
x
−
1
x
d
x
\int\frac{\sqrt{x-1}}{x}dx
∫xx−1dx
- 令 t = x − 1 t=\sqrt{x-1} t=x−1; x = t 2 + 1 x=t^2+1 x=t2+1, d x \mathrm{d}x dx= 2 t d t 2t\mathrm{d}t 2tdt
- ∫ x − 1 x d x \int\frac{\sqrt{x-1}}{x}dx ∫xx−1dx= ∫ t t 2 + 1 ⋅ 2 t d t \int{\frac{t}{t^2+1}}\cdot{2t}\mathrm{d}t ∫t2+1t⋅2tdt= 2 ∫ ( 1 − 1 t 2 + 1 ) d t 2\int{(1-\frac{1}{t^2+1}})\mathrm{d}t 2∫(1−t2+11)dt= 2 ( t − arctan t ) + C 2(t-\arctan{t})+C 2(t−arctant)+C= 2 ( x − 1 − arctan x − 1 ) + C 2(\sqrt{x-1}-\arctan{\sqrt{x-1}})+C 2(x−1−arctanx−1)+C
附加积分公式表
-
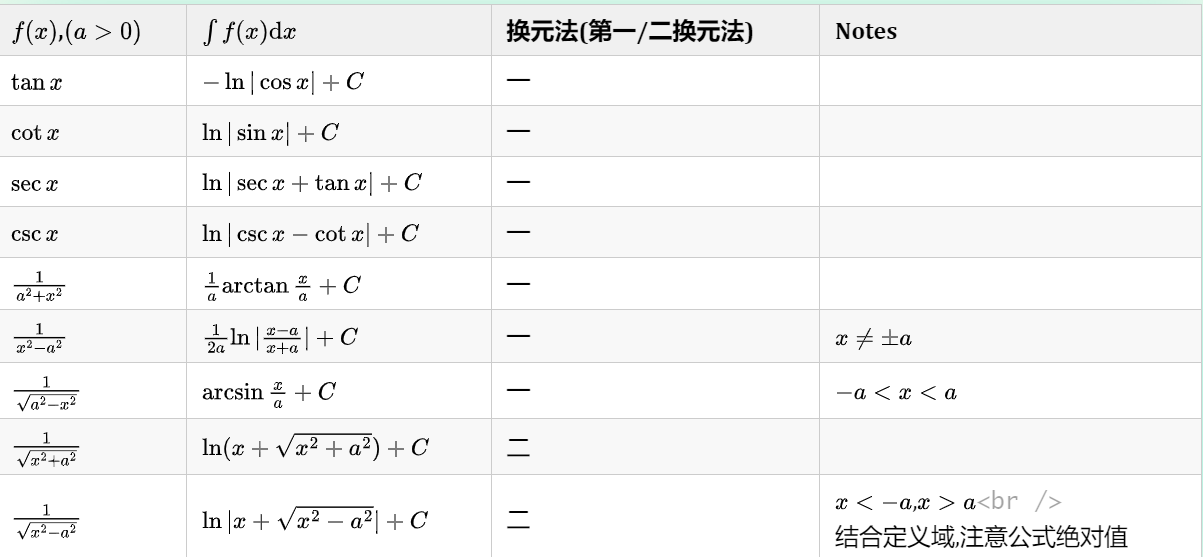
-
上述公式中有第二换元法推得的,而将它们作为积分公式后,则可以采用第一换元法的方式使用这些公式
-
高清版本(typora渲染)附末尾
例
-
∫ 1 4 x 2 + 9 d x \int{\frac{1}{\sqrt{4x^2+9}}}\mathrm{d}x ∫4x2+91dx= ∫ 1 ( 2 x ) 2 + 3 2 d x \int{\frac{1}{\sqrt{(2x)^2+3^2}}}\mathrm{d}x ∫(2x)2+321dx= 1 2 ∫ 1 ( 2 x ) 2 + 3 2 d ( 2 x ) \frac{1}{2}\int{\frac{1}{\sqrt{(2x)^2+3^2}}}\mathrm{d}(2x) 21∫(2x)2+321d(2x)= 1 2 ln ( 2 x + 4 x 2 + 9 ) + C \frac{1}{2}\ln(2x+\sqrt{4x^2+9})+C 21ln(2x+4x2+9)+C
-
∫ 1 1 + x − x 2 d x \int{\frac{1}{\sqrt{1+x-x^2}}}\mathrm{d}x ∫1+x−x21dx
- 一元二次多项式,总是可以配方成 ( x − a ) 2 + h (x-a)^2+h (x−a)2+h, ( h = ( c ) 2 ) (h=(\sqrt{c})^2) (h=(c)2)或 ( h = − c 2 ) (h=-\sqrt{c}^2) (h=−c2)
- 1 + x − x 2 1+x-x^2 1+x−x2= − ( x − 1 2 ) 2 + 5 4 -(x-\frac{1}{2})^2+\frac{5}{4} −(x−21)2+45= ( 5 4 ) 2 − ( x − 1 2 ) 2 (\sqrt{\frac{5}{4}})^2-(x-\frac{1}{2})^2 (45)2−(x−21)2
- ∫ 1 1 + x − x 2 d x \int{\frac{1}{\sqrt{1+x-x^2}}}\mathrm{d}x ∫1+x−x21dx= ∫ 1 ( 5 4 ) 2 − ( x − 1 2 ) 2 d x \int{\frac{1}{\sqrt{(\sqrt{\frac{5}{4}})^2-(x-\frac{1}{2})^2}}}\mathrm{d}x ∫(45)2−(x−21)21dx= ∫ 1 ( 5 4 ) 2 − ( x − 1 2 ) 2 d ( x − 1 2 ) \int{\frac{1}{\sqrt{(\sqrt{\frac{5}{4}})^2-(x-\frac{1}{2})^2}}}\mathrm{d}(x-\frac{1}{2}) ∫(45)2−(x−21)21d(x−21)= arcsin x − 1 2 5 / 2 + C \arcsin{\frac{x-\frac{1}{2}}{\sqrt{5}/2}}+C arcsin5/2x−21+C= arcsin 2 x − 1 5 + C \arcsin{\frac{2x-1}{\sqrt{5}}}+C arcsin52x−1+C
附
-
- | $f(x)$,$(a>0)$ | $\int{f(x)\mathrm{d}x}$ | 换元法(第一/二换元法) | Notes | | -------------------------- | ------------------------------------ | --------------------- | ------------------------------------------- | | $\tan{x}$ | $-\ln|\cos{x}|+C$ | 一 | | | $\cot{x}$ | $\ln|\sin{x}|+C$ | 一 | | | $\sec{x}$ | $\ln|\sec{x}+\tan{x}|+C$ | 一 | | | $\csc{x}$ | $\ln|\csc{x}-\cot{x}|+C$ | 一 | | | $\frac{1}{a^2+x^2}$ | $\frac{1}{a}\arctan{\frac{x}{a}}+C$ | 一 | | | $\frac{1}{x^2-a^2}$ | $\frac{1}{2a}\ln|\frac{x-a}{x+a}|+C$ | 一 | $x\neq{\pm a}$ | | $\frac{1}{\sqrt{a^2-x^2}}$ | $\arcsin{\frac{x}{a}}+C$ | 一 | $-a<x<a$ | | $\frac{1}{\sqrt{x^2+a^2}}$ | $\ln(x+\sqrt{x^2+a^2})+C$ | 二 | | | $\frac{1}{\sqrt{x^2-a^2}}$ | $\ln|x+\sqrt{x^2-a^2}|+C$ | 二 | $x<-a$,$x>a$<br />结合定义域,注意公式绝对值 | -
f ( x ) f(x) f(x), ( a > 0 ) (a>0) (a>0) ∫ f ( x ) d x \int{f(x)\mathrm{d}x} ∫f(x)dx 换元法(第一/二换元法) Notes tan x \tan{x} tanx $-\ln \cos{x} +C$ cot x \cot{x} cotx $\ln \sin{x} +C$ sec x \sec{x} secx $\ln \sec{x}+\tan{x} +C$ csc x \csc{x} cscx $\ln \csc{x}-\cot{x} +C$ 1 a 2 + x 2 \frac{1}{a^2+x^2} a2+x21 1 a arctan x a + C \frac{1}{a}\arctan{\frac{x}{a}}+C a1arctanax+C 一 1 x 2 − a 2 \frac{1}{x^2-a^2} x2−a21 $\frac{1}{2a}\ln \frac{x-a}{x+a} +C$ 1 a 2 − x 2 \frac{1}{\sqrt{a^2-x^2}} a2−x21 arcsin x a + C \arcsin{\frac{x}{a}}+C arcsinax+C 一 − a < x < a -a<x<a −a<x<a 1 x 2 + a 2 \frac{1}{\sqrt{x^2+a^2}} x2+a21 ln ( x + x 2 + a 2 ) + C \ln(x+\sqrt{x^2+a^2})+C ln(x+x2+a2)+C 二 1 x 2 − a 2 \frac{1}{\sqrt{x^2-a^2}} x2−a21 $\ln x+\sqrt{x2-a2} +C$