了解
一、函数的性质



理解
一、函数
1、函数概念

⚠️定义域和对应规则是同一函数的判断
2、复合函数

简单的说就是内层函数的值域与外层函数的定义域有交集
3、反函数

3.1、y=x^3为反函数,y=x^2不是
3.2、单调函数是反函数的充分非必要条件(单调函数一定有反函数)例如反函数不一定单调

3.3、反函数之间的等式
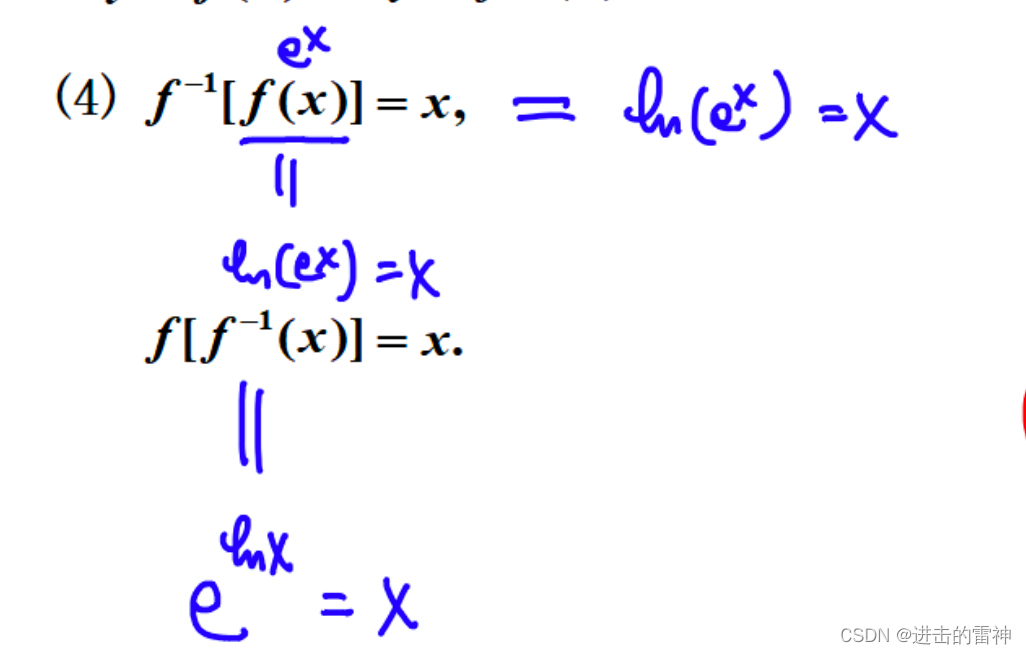
掌握
一、基本初等函数

1、幂函数y=x^a(a为常数)
1.1、性质
- 幕函数的图像最多只能同时出现在两个象限,且不经过第四象限;如图与坐标轴相交,则交点一定是坐标原点
- 所有幕函数在(0,+00)上都有定义,并且图像都经过点(1,1)。
- 当a≤-1且a为奇数时,函数在第一、第三象限为减函数
- 当a≤-1且a为偶数时,函数在第二象限为增函数
- 当a=0且x不为0时,函数图象平行于x轴且y=1、但不过(0,1)
- 当a=1时,函数图像为过(0,0),(1,1)且关于原点对称的射线
- 当0<a<1时,函数是增函数
- 当a≥1且a为奇数时
1.2、图形(常见的幂函数)
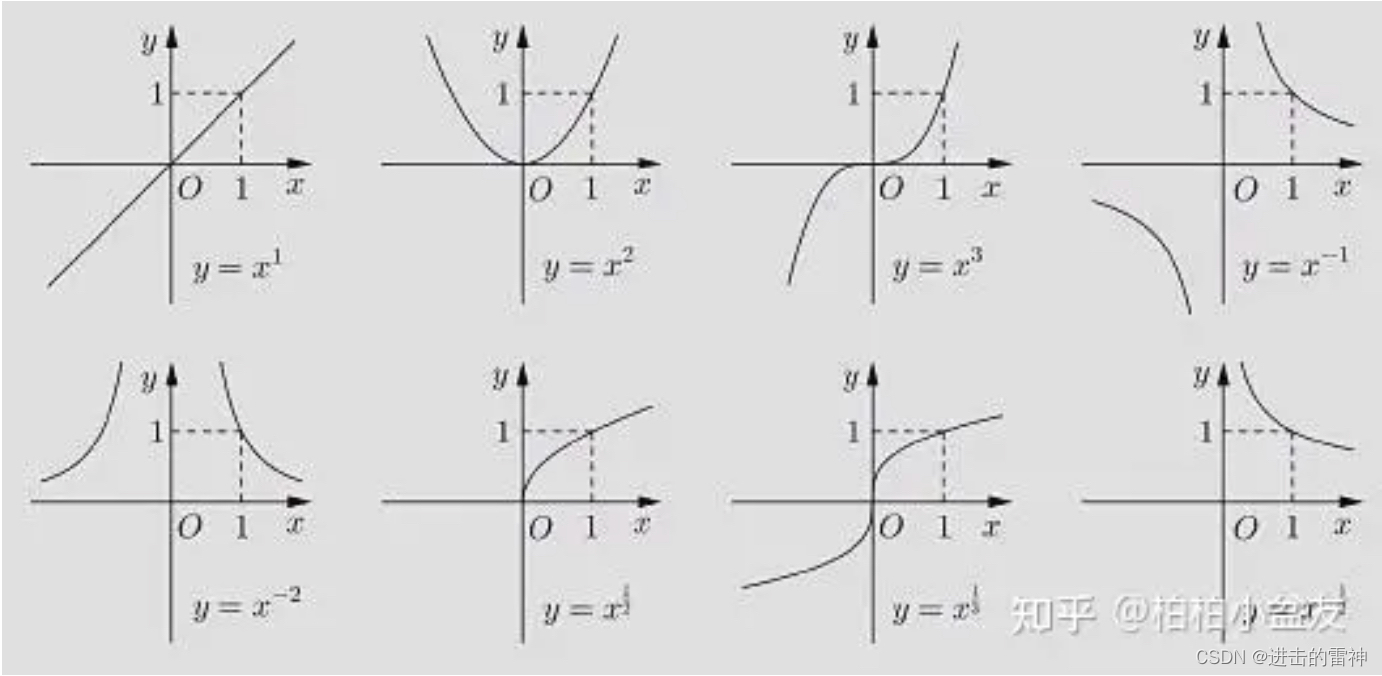
2、指数函数y=a^x(a>0且a≠1)
2.1、性质
- 指数函数y=a^x(a>0且a≠1)的函数值恒大于零,定义域为R,值域为(0,+00)
- 指数函数y=a^x(a>0且a≠1)的图像经过点(0,1)
- 指数函数y=a^x(a>1)在R上递增,指数函数y=a^x(0 <a< 1)在R上递减
- 函数总是在某一个方向上无限趋向于X轴,并且永不相交。
- 函数总是通过(0,1)这点,(若 ,则函数定过点(0,1+b))
- 指数函数无界
- 指数函数是非奇非偶函数
- 指数函数具有反函数,其反函数是对数函数
2.2、图形
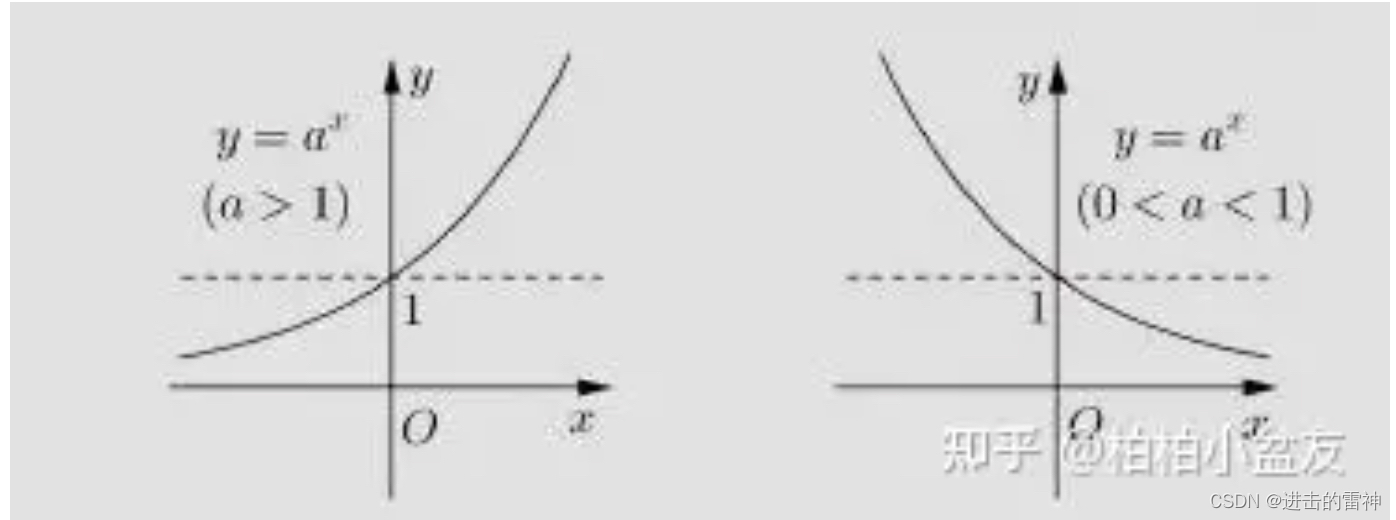
3、对数函数y=logaX(a>0,且a≠1)
3.1、性质
- 定义域:对数函数y=log ax 的定义域是{x 丨x>0};
- 定点 :对数函数的函数图像恒过定点(1,0);
- 单调性 :a>1时,在定义域上为单调增函数; 0<a<1时,在 定义域上为单调减函数;
- 零点:x=1
一般地
- 对数函数y=logax(a>0且a≠1)就是指数函数y=a^x(a>0且a≠1)的反函数。
- 因为指数函数y=a^x(a>0且a≠1)的值域是(0,+00)
- 所以对数函数y=logax(a>0且a≠1)的定义域是(0,+00)。
3.2、图形
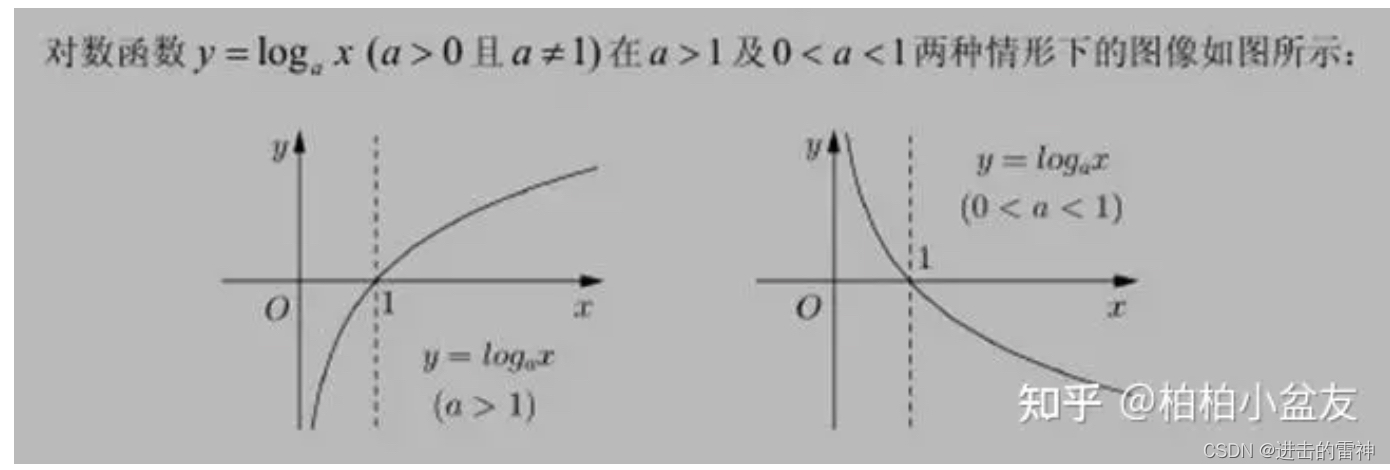
3.3、对数运算性质
如果a>0,a≠1,M>0,N>0,那么:

- (1)对数:一般地,如果a(a>0,a≠1)的b次幕等于N,即a^b=N,那么b叫做以a为底N的对数;记作:logaN =b,其中a叫做对数的底数,N叫做真数。
- (2)常用对数:lg(b)=log 10b(10为底数);
- (3) 自然对数:ln(b)=log eb(e为底数) e为 无限不循环小数,通常情况下只取e=2.71828。
4、三角函数
4.1、y=sinx(正弦)与y=cos x(余弦)函数的图像与性质
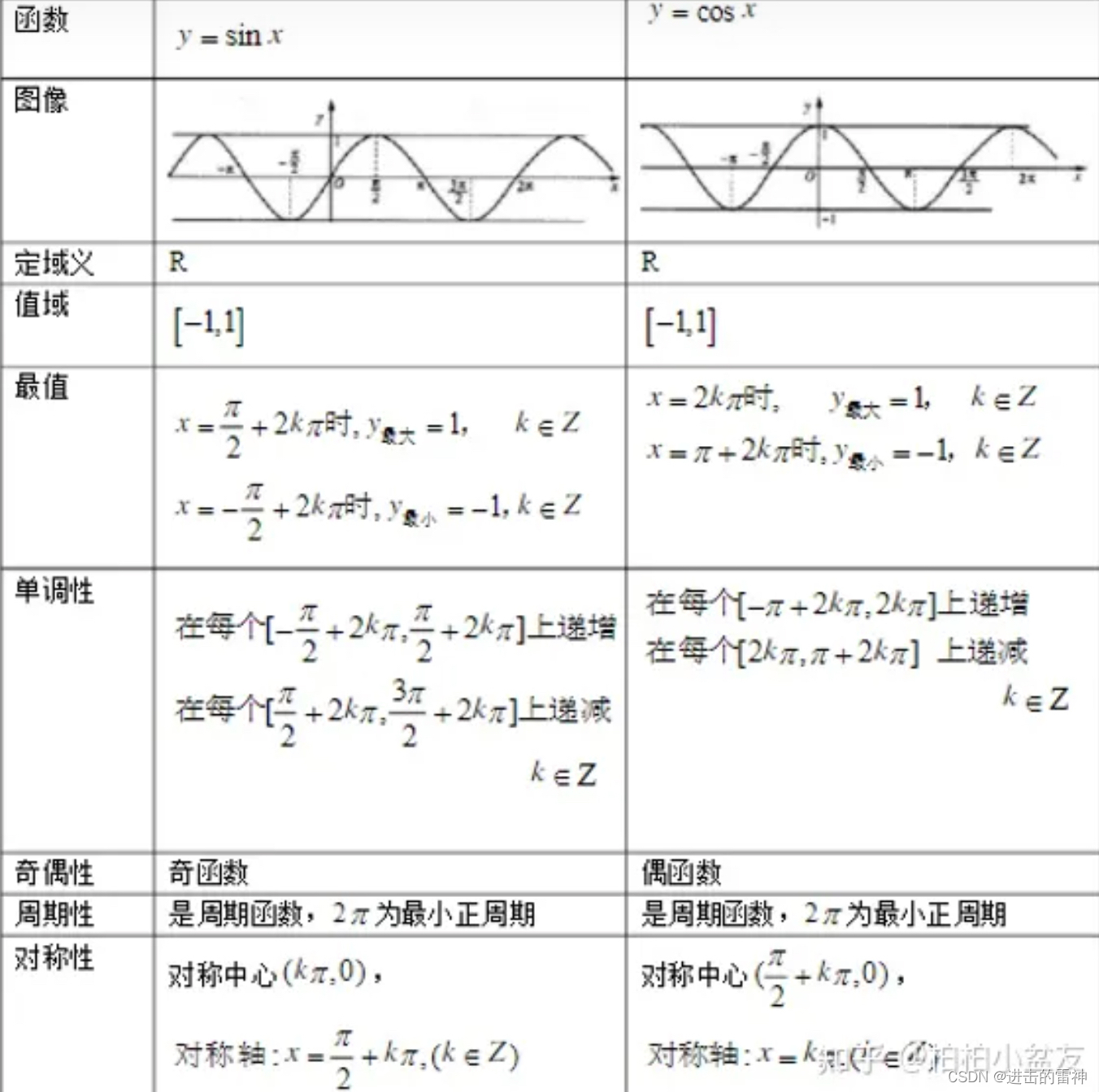
4.2、y=tan x(正切)与y=cotx(余切)函数的图像与性质
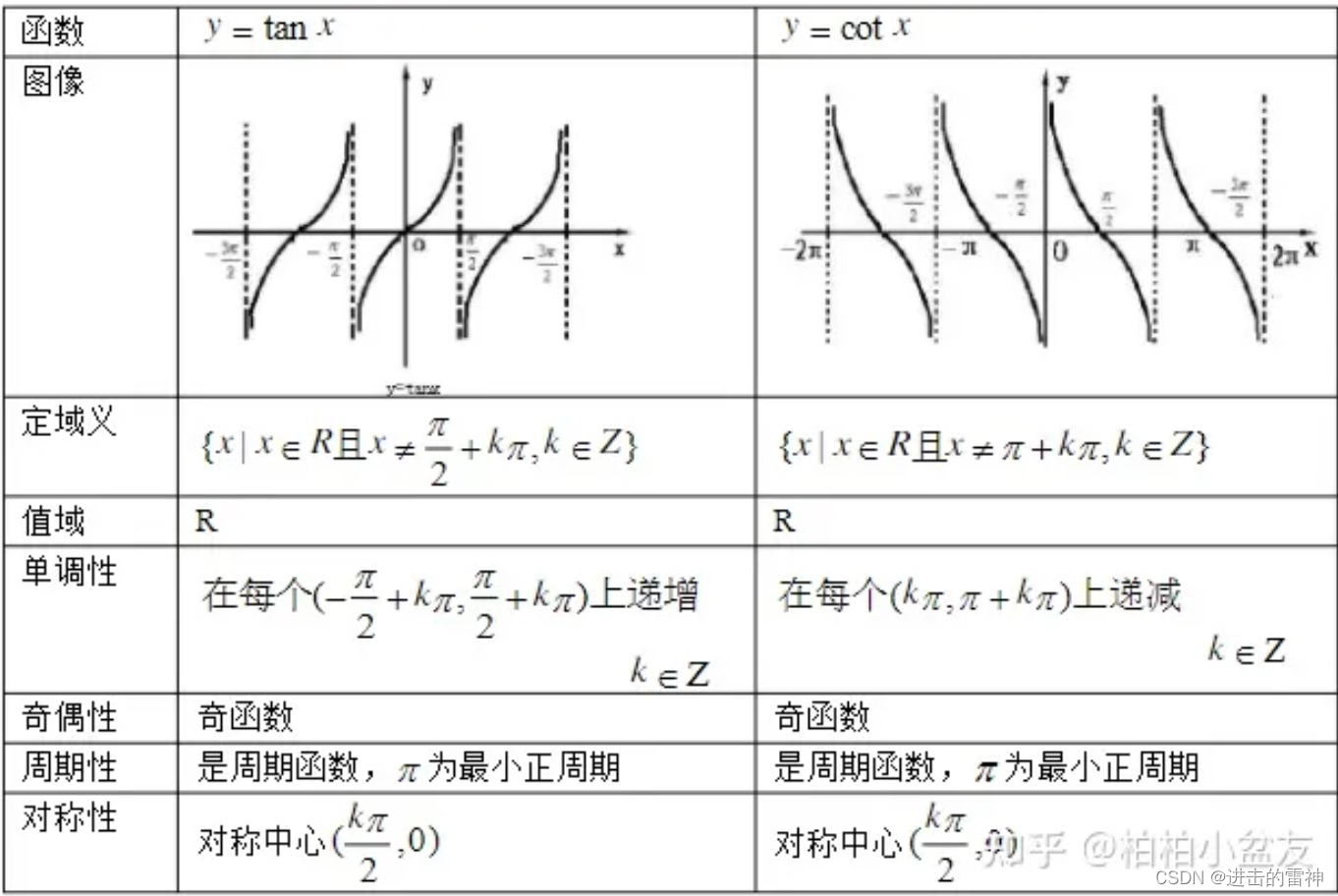
5、反三角函数
5.1、y=arcsin x(反正弦)与y = arccos x(反余弦)函数的图像与性质
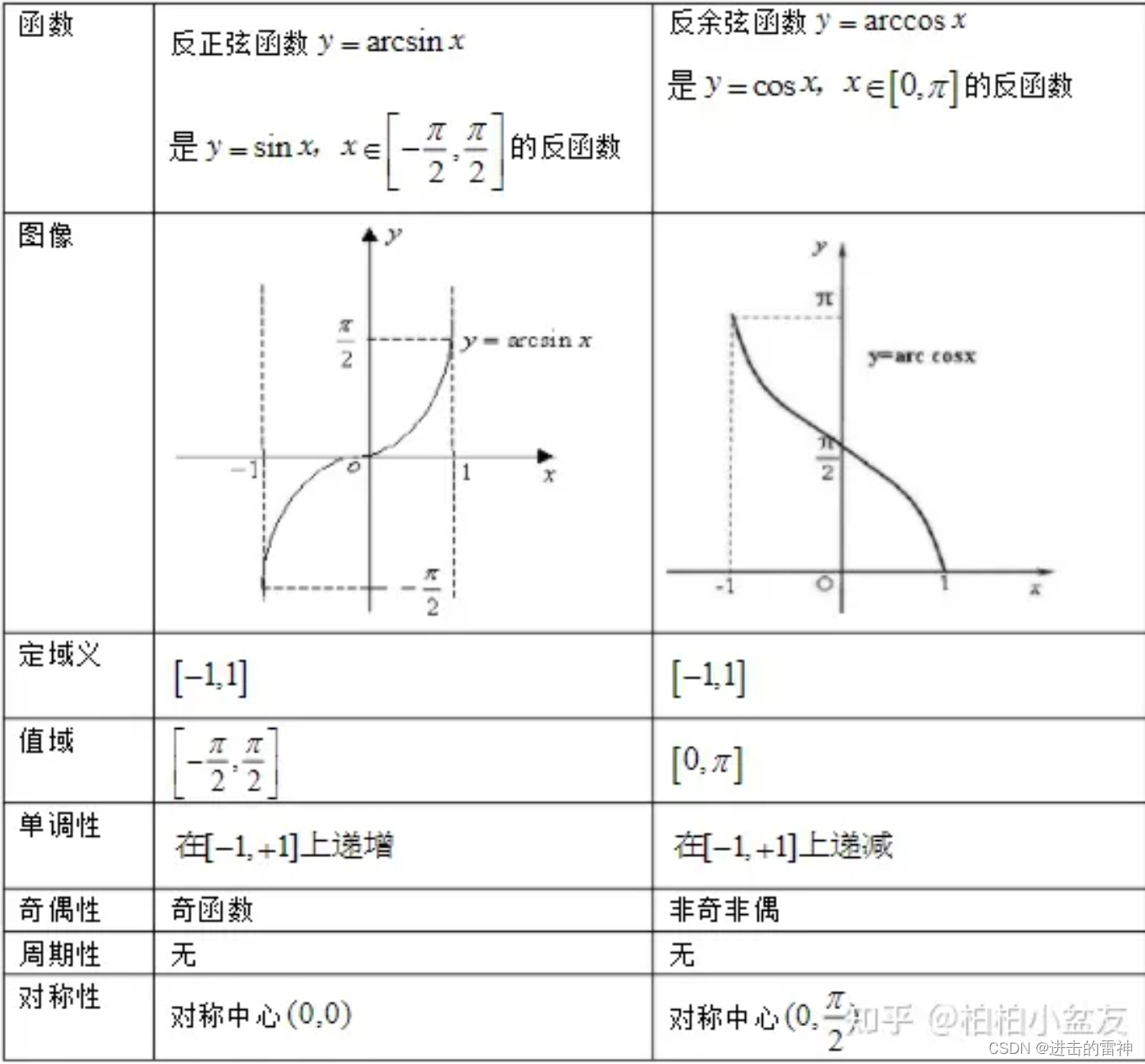
5.2、y= arctan x(反正切)与y = arccot x(反余切)函数的图像与性质