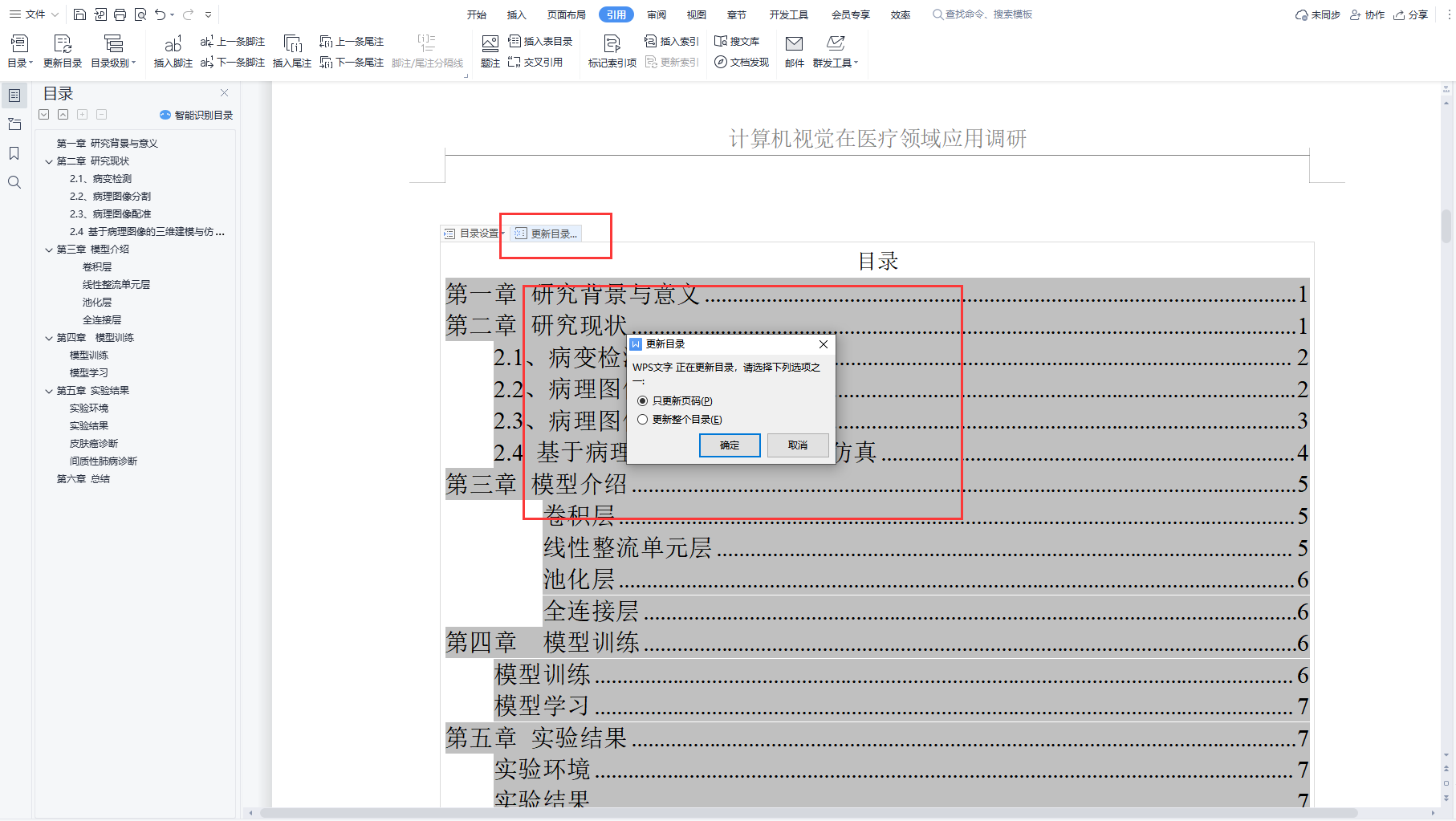
前言

众所周知，字符串查找的应用范围非常广，网页上有各式各样的浏览器搜索，再到编程需要的vsCode或vsStudio都自带了搜索功能；一个查找算法的优劣可以直接影响用户的搜索体验如何
但鉴于暴力搜索算法的O(m * n)复杂度，就有了K姓大佬，M姓大佬，P姓大佬设计出来的一套O(n + m)字符串查找算法；于是他们的名字被载入史册，且这套算法被命名为KMP算法
leetcode指路：找出字符串中第一个匹配项的下标

刚接触KMP算法时，你大概会觉得这个算法非常诡异，一波诡异的操作处理后生成了一个next数组，又一波诡异的遍历操作后，就找到了目标位置(？？？WTF)；
代码倒是不长，每个单词都认识，但是放一块就不认识了，像极了四级英语阅读。。

一、需要提前明白的概念

1. 最大前后缀

首先你需要知道最大前后缀是什么；

最大前后缀就是 在一段字符串中，从首尾分别开始，可能形成的最大相等字符子串

以下图为例：在箭头位置上，它的前置最大前后缀为abb
图1.1

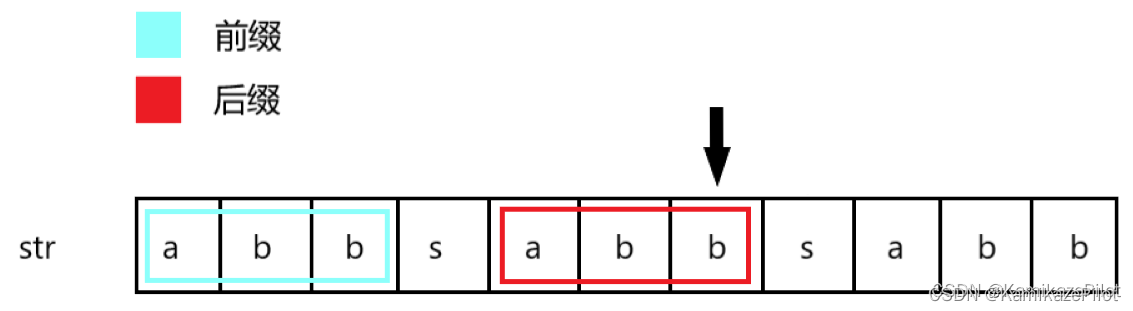
以下图为例：在箭头位置上，它的前置最大前后缀为abbsab
图1.2

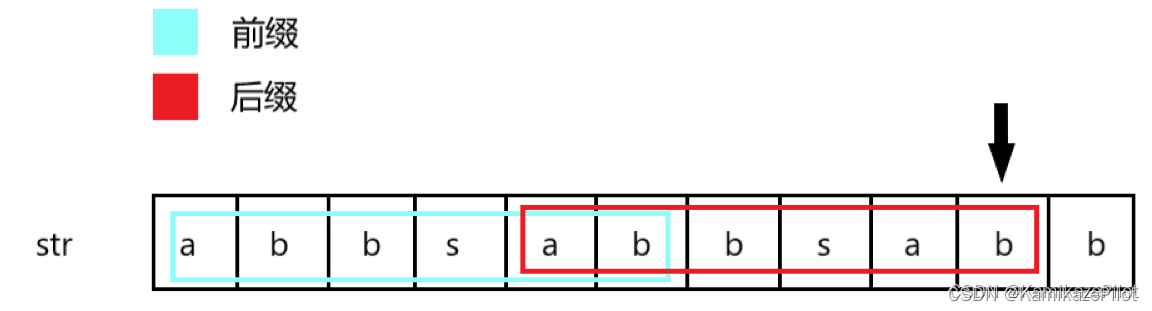
看到这里你可能会有疑惑，最大前后缀的规则是什么？下面简单进行一个总结：

最大前缀与最大后缀必须相等。
最大前后缀必须小于它可取的长度；即：图一中最大前后缀不能同时取abbsabb（s以前的所有字符），图二中最大前后缀不能取b以前的所有字符，那样的话就失去了它的意义。
最大前后缀必须尽可能的长；图二中可能相等的前后缀有：ab、abbsabb，我们需要取其中较大的那个。

2. `next`数组

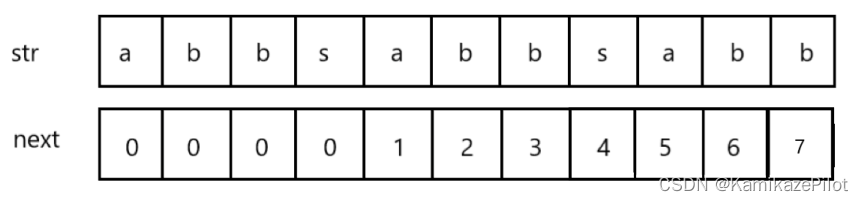
next数组专门用于保存字符串的每个位置之前，它的最大前后缀长度
比如在刚刚的那个字符串所对应的next数组
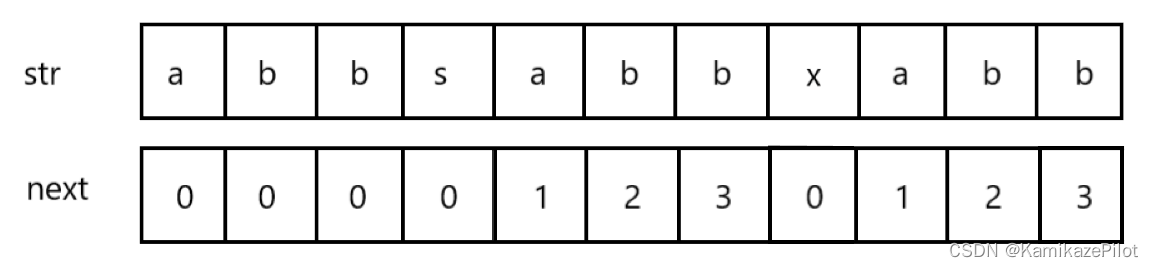
再举一个例子：
它的每个位置，都记录着在它位置之前的子串中的最大前后缀长度。

至于next数组是哪里来的，有什么用？会放在后面讲。

二、主逻辑

1.主要步骤：

这里先展示一下如何使用最大前后缀

比如有字符串str1 和 str2，要求在str1中查找str2位置；（这里的字符串跟上面关于next讲解的部分的没关系，千万不要搞混了）
首先假设我们已经得到了str2的正确的next数组
那么我们怎么通过已知的信息来对暴力解法进行优化呢？
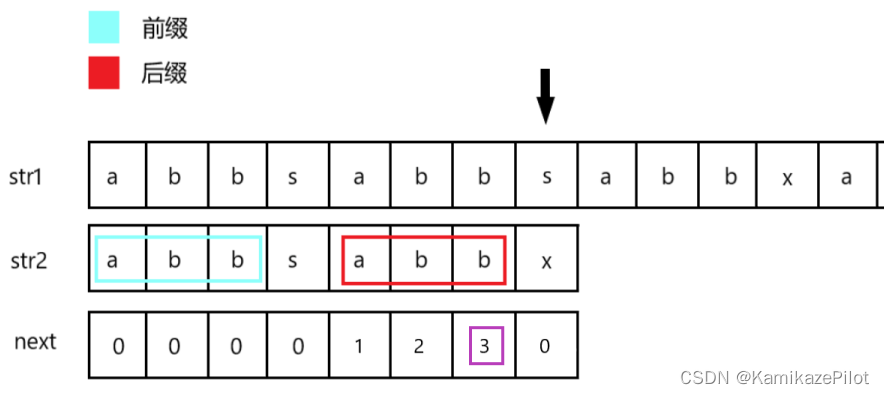
经过之前7个字符的比较，指针顺利来到了s位置
此时发现该位置两个该位置不匹配，那咋办？
此时我们已经知道了str2的next数组中，x位置上的前置子串最大前后缀长度为3
那这是不是代表，我把str2字符串向前移到相对应得位置，那么此时str1和str2得前缀依然是匹配上了：

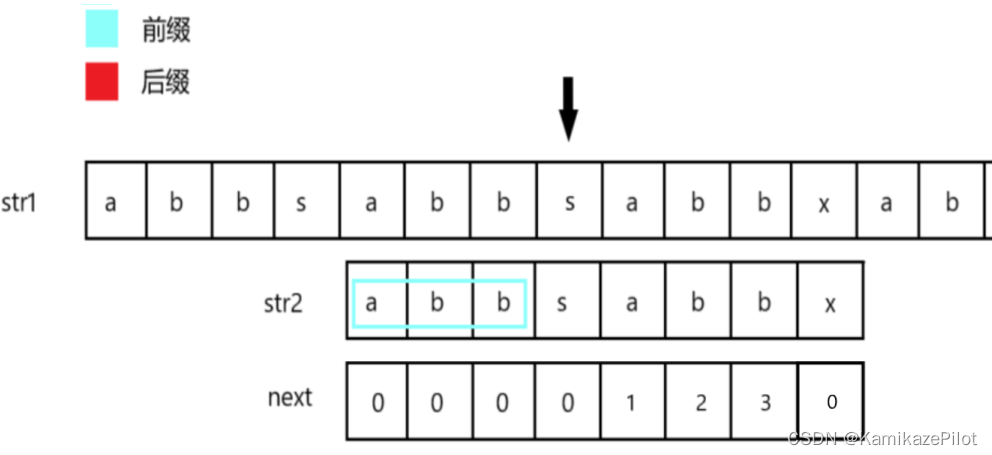
这一步，过滤了暴力解法的主串指针回溯过程
那么为什么可以这么跳过呢？
主要分两个证明：

前后缀相等，则字符串跳转后，下标位置处前字串也一定匹配
跳转经过的区间内，一定不存在与主串匹配的存在

问题一自不用说，肉眼可见，下面主要证明步骤2；为什么经过区间一定不含可能匹配的存在

假设：如果在经过区间上存在可匹配的存在，那么将说明此时该区间内存在更大的前后缀，这与next数组中的已求得数据不符，所以该结论不成立。

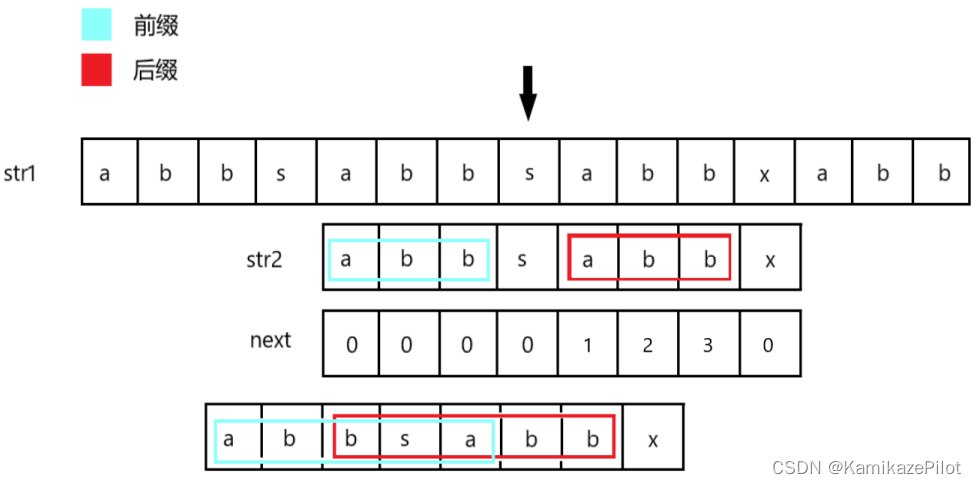
2.跳跃方式

跳跃到哪个位置将由next数组决定，next数组与str2共用一个下标，需要查询前缀位置直接在next的对应下标位置寻找
例如下图中，在箭头位置首次匹配失败，通过直接查询next数组中 x的对应位置找到需要跳转的下标。
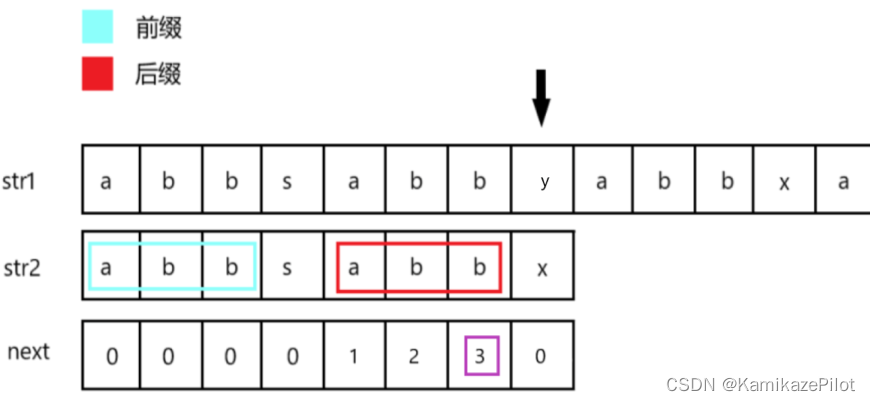
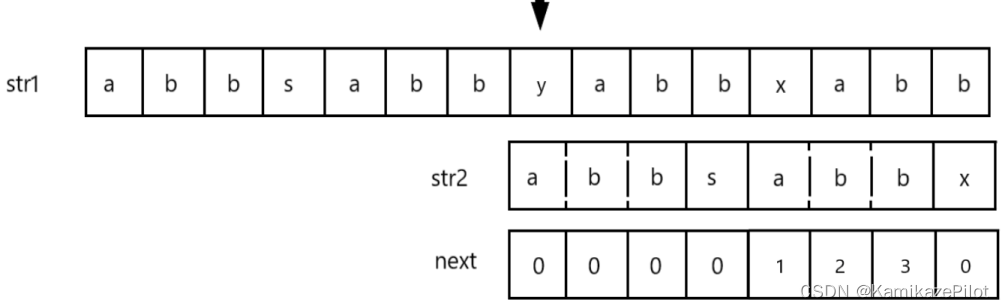
这里还匹配失败如下图：
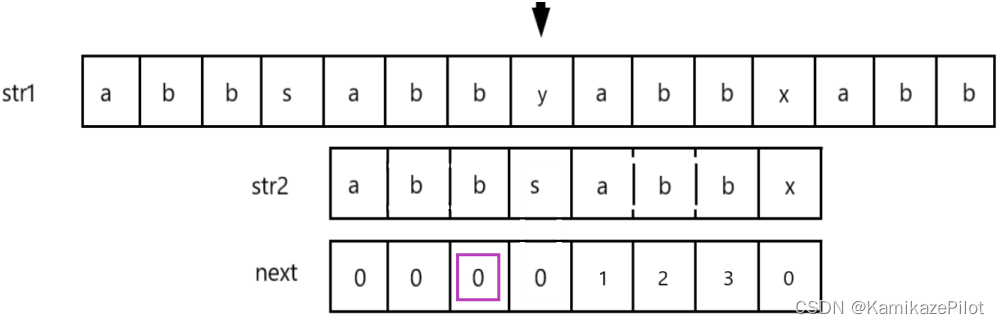
那么这里就再次进行跳转，跳转到0位置继续匹配
如果str2指针已经跳到0位置，还匹配失败的话，就挪动主串指针：

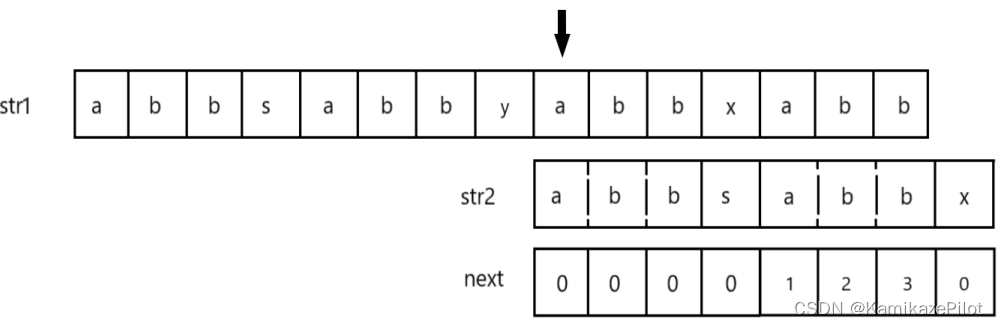
以上就是主串的整个匹配过程。
计算可得：这个过程的最大时间复杂度不超过O(2 * N)

3.主要代码

int strStr(string str1, string str2) {
        vector<int> next;
        func(next, str2);					//求next数组

        int idx1 = 0;
        int idx2 = 0;
        while(idx1 < str1.size())
        {
            if(str1[idx1] == str2[idx2])	//匹配上就两个指针一起往下走
            {
                idx1++;
                idx2++;
                if(idx2 == str2.size())
                {
                    return idx1 - idx2;
                }
            }
            else if(idx2 == 0)				//没匹配上而且idx2在0位置
            {
                idx1++;
            }
            else{							//没匹配上  idx2不在0位置
                idx2 = next[idx2];
            }
        }
        return -1;
    }

三、求`next`数组

求next数组所用的是经典的动态规划过程，简单来说就是两个指针一个在头部找前缀，一个指针在尾部找后缀。
这里不能使用暴力求解的方法，因为暴力求解的最高时间复杂度为O(m ** 2)，那么在某些极端情况下，整个算法的时间复杂度会涨到O(n ** 2)

1.总过程

我不论如何，先给next数组填一个0
图3.1

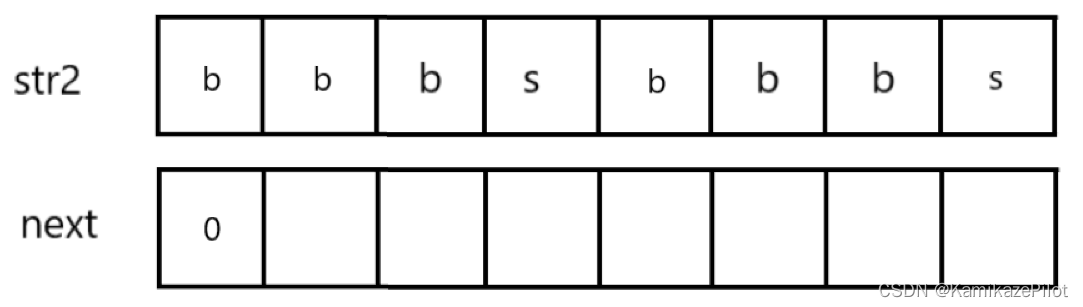
为啥这么做呢？是因为下标0位置不包含前缀，而且这一位也不会被访问到，我们真正开始计算next数组是从1号下标开始。
创建两个指针，分别寻找前缀和后缀，这里用颜色区分。
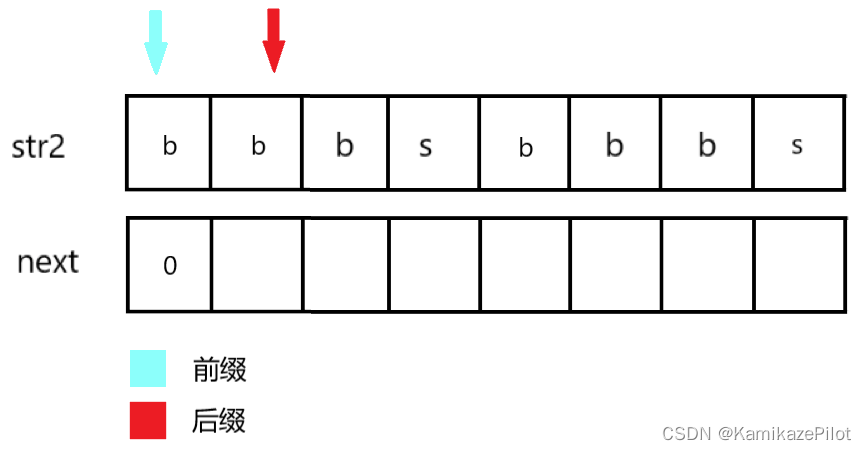
第一步发现：两个字符相等，那么都自增，后缀位置next数组内填(前缀指针下标 + 1)即(0 + 1)
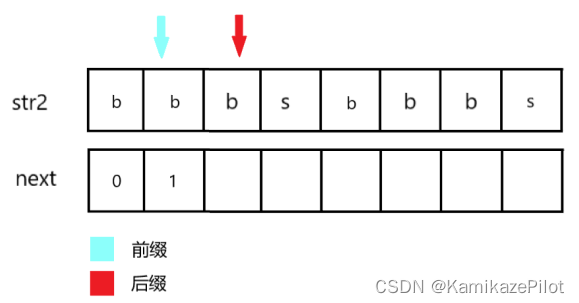
第二步发现：还相等，重复上过程
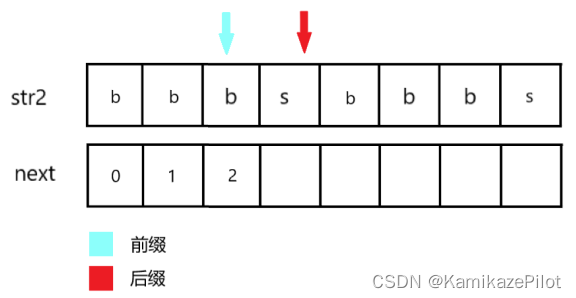
第三步发现：她两不相等，那么就通过已知最大前缀数来找到需要跳转到的位置：next[1] == 1
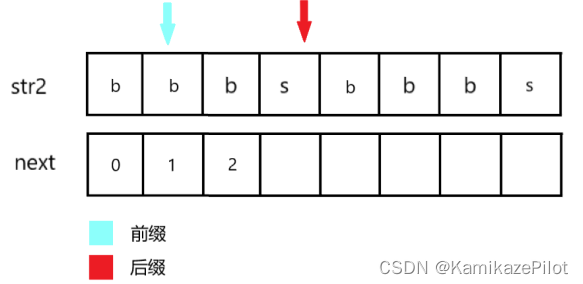
第四步发现：她两还不相等，那么通过已知最大前缀数来找到需要跳转到的位置：next[0] == 0
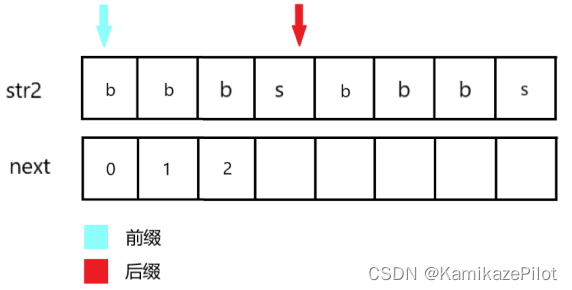
此时发现她两还不相等，但是前缀下标已经走到了0位置，所以说明s位置不存在任何可以匹配的相等前后缀，就给该位置赋 0 然后后缀指针自增

图3.7
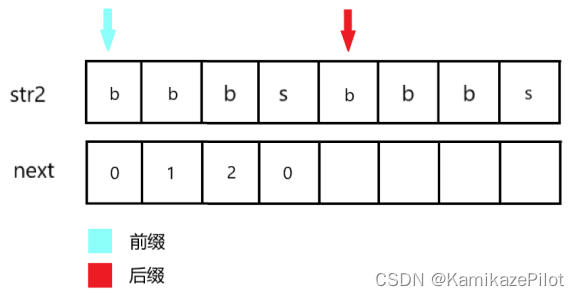
继续重复上述过程：
图3.8
图3.9
图3.10
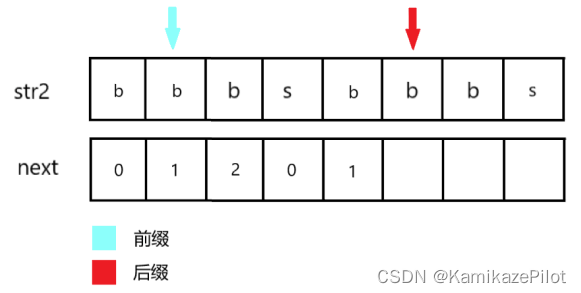
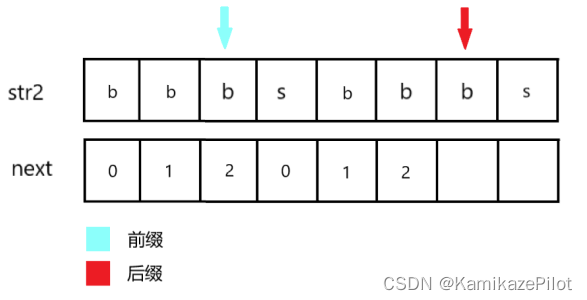
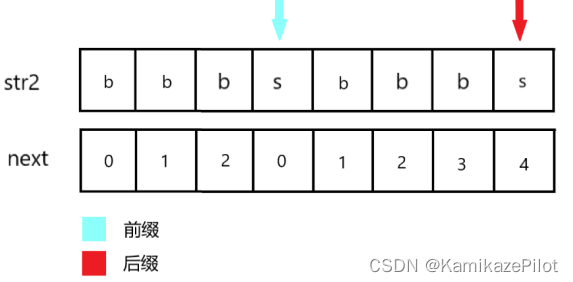
以上就是整个next数组的求解过程，主要采用动态规划的形式，以类似主逻辑的方式将整个next数组求解。

四、代码

class Solution {
    //求next 数组
    void func(vector<int>& next, string& str2)
    {
        next.resize(0);
        next.push_back(0);
        int idx1 = 1;
        int idx2 = 0;
        while(idx1 < str2.size())
        {
            //相等则next填充，两指针自增
            if(str2[idx1] == str2[idx2])
            {
                next.push_back(++idx2);
                idx1++;
            }//格式串在最左部，
            else if(idx2 == 0)
            {
                next.push_back(0);
                idx1++;
            }
            else{//可以向前找
                idx2 = next[idx2 - 1];
            }
        }
    }
public:
	int strStr(string str1, string str2) {
        vector<int> next;
        func(next, str2);					//求next数组

        int idx1 = 0;
        int idx2 = 0;
        while(idx1 < str1.size())
        {
            if(str1[idx1] == str2[idx2])	//匹配上就两个指针一起往下走
            {
                idx1++;
                idx2++;
                if(idx2 == str2.size())
                {
                    return idx1 - idx2;
                }
            }
            else if(idx2 == 0)				//没匹配上而且idx2在0位置
            {
                idx1++;
            }
            else{							//没匹配上  idx2不在0位置
                idx2 = next[idx2];
            }
        }
        return -1;
    }
}