一定要读 真的是不一样的收获啊

不知道 屏幕前的各位get到了没有

Hinton et al. (2015) introduced the idea of temperature in the softmax outputs to better represent smaller probabilities in the output of a single sample. 

Hinton等人(2015)引入了softmax输出中温度的思想，以更好地表示单个样本输出中的较小概率。

These smaller probabilities provide useful information about the learned representation of the teacher model; some tradeoff between large temperatures (which increase entropy) or small temperatures tend to provide the highest transfer of knowledge between student and teacher.

这些较小的概率提供了有关教师模型学习表示的有用信息；高温（增加熵）或低温之间的一些权衡往往提供学生和教师之间知识的最高转移。

soft target 的work

Attention transfer (Zagoruyko & Komodakis, 2016a) focuses on the features maps of the network as opposed to the output logits. Here the idea is to elicit similar response patterns in the teacher and student feature maps (called "attention").

注意力转移 (Zagoruyko & Komodakis, 2016a) 专注于网络的特征图，而不是输出 logits。在这里，这个想法是在教师和学生特征图（称为“注意力”）中引出类似的响应模式。

resolution can be combined in this approach, which is a significant limitation since it requires student and teacher networks with very similar architectures.

这种方法可以结合分辨率，这是一个重大限制，因为它需要具有非常相似架构的学生和教师网络。

FitNets (Romero et al., 2014) also deal with intermediate representations by using regressions to guide the feature activations of the student network.FitNets (Romero et al., 2014) 还通过使用回归来指导学生网络的特征激活来处理中间表示。

这一段比较关键

我们在本文中使用的对比目标与 CMC 中使用的对比目标相同（Tian et al., 2019）。

但是我们从不同的角度推导出，并给出了一个严格的证明，即我们的目标是互信息的下界。

我们的目标也与 (Oord et al., 2018; Gutmann & Hyvärinen, 2010) 中介绍的 InfoNCE 和 NCE 目标有关。Oord等人(2018)在自监督表示学习的背景下使用对比学习。

他们表明，他们的目标最大化互信息的下界。(Hjelm et al., 2018) 中使用了一种非常相关的方法。InfoNCE和NCE密切相关，

但与对抗学习不同(Goodfellow et al.， 2014)。

在 (Goodfellow, 2014) 中，表明 Gutmann &

Hyvärinen (2010) 的 NCE 目标可以导致最大似然学习，而不是对抗性目标。

对比目标鼓励教师和学生将相同的输入映射到接近表示（在某些度量空间中），以及远距离表示的不同输入，如阴影圆圈所示。

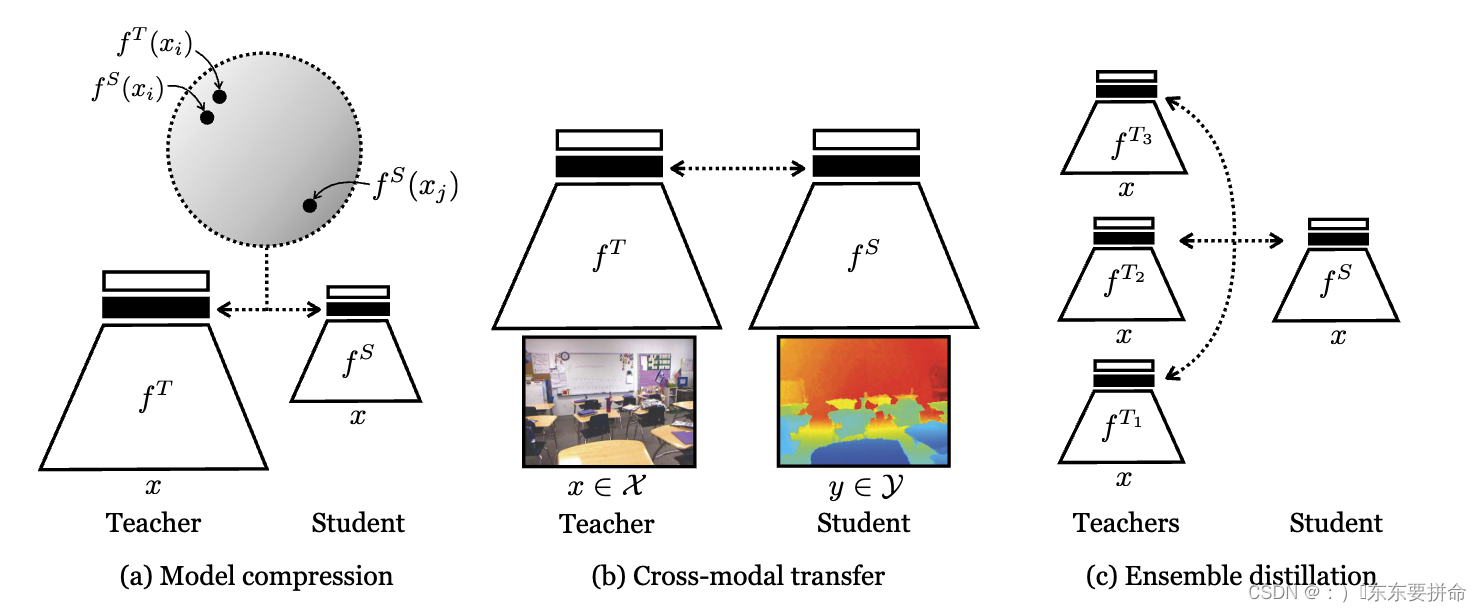
让我们深入探讨对比损失（Contrastive Loss）的细节：

对比损失的核心思想是将相似的样本拉近，将不相似的样本推远。在这篇论文中，对比损失被用来最大化教师和学生表示之间的互信息。

互信息度量了两个随机变量之间的相互依赖性。在这里，我们可以将教师和学生的表示视为两个随机变量。互信息的定义基于边际分布和条件分布。

• 边际分布：它描述了单个随机变量的概率分布，不考虑其他随机变量。例如，教师或学生的表示的概率分布。

• 条件分布：给定一个随机变量的值，它描述了另一个随机变量的概率分布。例如，给定教师的表示，学生的表示的概率分布。

互信息度量了从边际分布到条件分布的信息增益。在对比损失中，我们希望最大化这种增益，这意味着学生的表示应该尽可能地捕获教师表示中的信息。

为了实现这一目标，对比损失将相似的表示（例如，来自同一个样本的教师和学生的表示）拉近，而将不相似的表示（例如，来自不同样本的表示）推远。

互信息（Mutual Information, MI）是信息论中的一个概念，用于量化两个随机变量之间的相互依赖性。它度量了通过观察一个随机变量而获得的关于另一个随机变量的信息量。

假设我们有两个随机变量 X 和 Y，它们的联合分布如下：

X\Y	y1​	y2​
x1​	0.2	0.3
x2​	0.1	0.4

这个表格表示的是 X 和 Y 的所有可能的组合的概率。

边际分布

边际分布是从联合分布中得到的，它表示的是一个随机变量的分布，而不考虑其他随机变量。

对于 X 的边际分布：

• p(X=x1)=0.2+0.3=0.5 P(X=x1​)=0.2+0.3=0.5
• p(X=x2)=0.1+0.4=0.5 P(X=x2​)=0.1+0.4=0.5

对于 Y 的边际分布：

• p(Y=y1)=0.2+0.1=0.3P(Y=y1​)=0.2+0.1=0.3
• p(Y=y2)=0.3+0.4=0.7P(Y=y2​)=0.3+0.4=0.7

条件分布

条件分布表示的是在给定一个随机变量的值的情况下，另一个随机变量的分布。

例如，给定X=x1​ 的条件下 Y 的分布：

• p(Y=y1∣X=x1)=0.20.5=0.4 P(Y=y1​∣X=x1​)=0.50.2​=0.4
• p(Y=y2∣X=x1)=0.30.5=0.6 P(Y=y2​∣X=x1​)=0.50.3​=0.6

这意味着，如果我们知道 X=x1​，那么 Y 取 y1​ 的概率是0.4，取 y2​ 的概率是0.6。

同样，我们可以计算给定 X=x2的条件下Y 的分布。

这个表格表示的是 X 和 Y 的所有可能的组合的概率。例如，p(X=x1,Y=y1)=0.2。P(X=x1​,Y=y1​)=0.2，这意味着 X 取值 x1​ 和 Y 取值 y1​ 的联合概率是0.2。

互信息的定义是基于边际分布、条件分布和联合分布的：

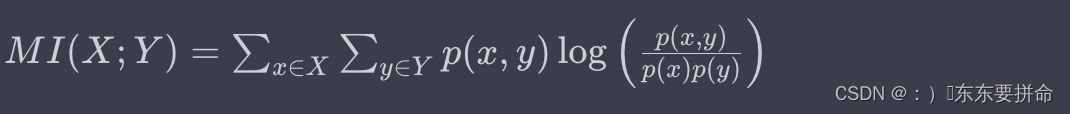
从直观上讲，互信息度量了以下内容：

• 如果 X 和 Y 完全独立，那么它们之间的互信息为0，因为知道一个变量的值并不提供关于另一个变量的任何信息。
• 如果 X 和 Y 完全相关（例如，一个是另一个的函数），那么互信息将是最大的，因为知道一个变量的值完全确定了另一个变量的值。

在对比损失中，我们希望最大化这种增益（X，Y相关的程度大一些），这意味着学生的表示应该尽可能地捕获教师表示中的信息。

总之，互信息是一个度量两个随机变量之间相互依赖性的指标，它基于边际分布、条件分布和联合分布来定义。

为了实现这一目标，对比损失将相似的表示（例如，来自同一个样本的教师和学生的表示）拉近，而将不相似的表示（例如，来自不同样本的表示）推远。

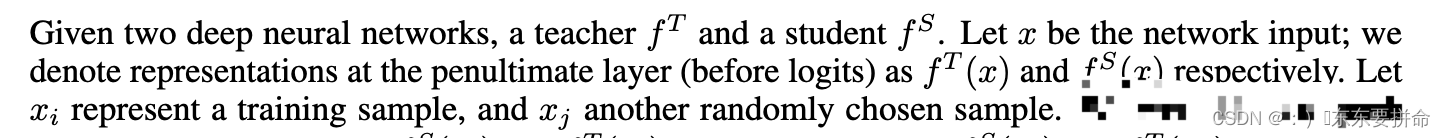
这里的表示默认大家会了啊

我们还要知道

例如，考虑两个随机变量：一个是你明天是否会吃早餐（是或否），另一个是明天是否会下雨（是或否）。如果这两个事件是独立的（即吃早餐与下雨无关），那么你吃早餐和明天下雨的联合概率就是你吃早餐的概率乘以明天下雨的概率。

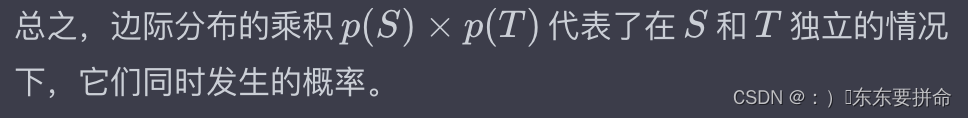
by maximizing KL divergence between these distributions, we can maximize the mutual information between student and teacher representations.

通过最大化这些分布之间的 KL 散度，我们可以最大化学生和教师表示之间的互信息。

这句话很好理解哈，首先要知道的是KL散度是衡量两个分布的接近程度的，

所以如何接近呢 就要设计实现这一目标的损失函数了

c=0 X ，Y完全独立 ；c =1 可以看相互依赖性（我也不知道对不对）

现在，假设在我们的数据中，我们为每个 N 个不一致对（来自联合分布，即提供给 T 和 S 的相同输入）被赋予 1 个一致的对（来自边缘的乘积；提供给 T 和 S 的独立随机抽样输入）。

这句话虽然是中文 但是有点看不懂

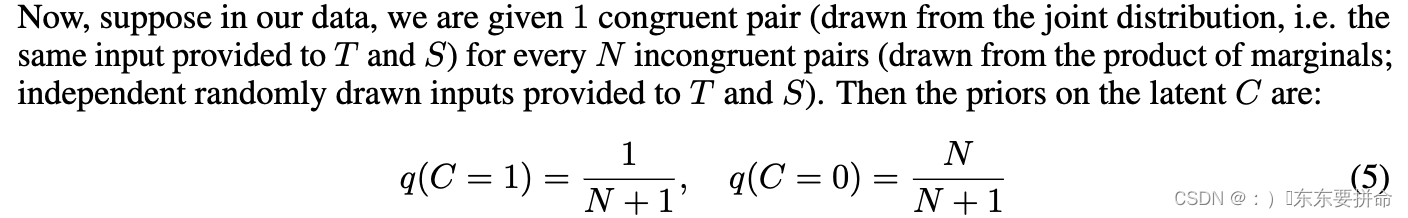
简而言之，先验分布表示我们的初始经验，而后验分布表示在考虑新数据后的更新后的知识。

他让我们算 后验分布 

我给你们推啊 

很简单 相信你们看的懂的

这个放缩是咋放出来的呀

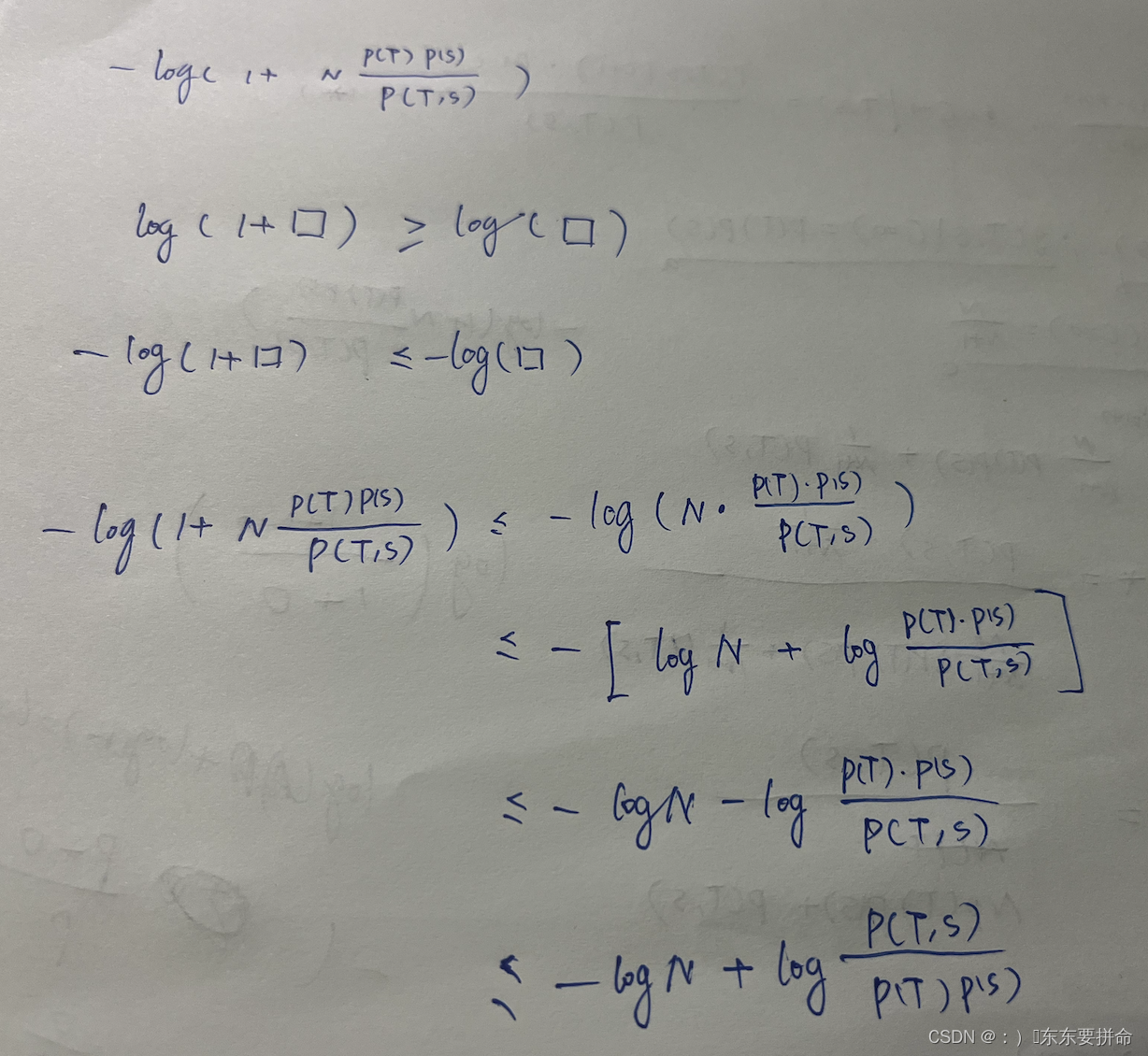
然后移项

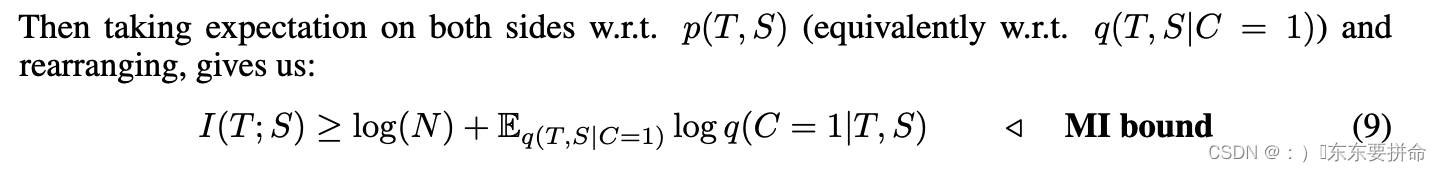
这个东西眼熟不 互信息的重要组成部分

Thus maximizing Eq(T,S|C=1) log q(C = 1|T, S) w.r.t. the parameters of the student networkS increases a lower bound on mutual information.

学生网络的参数增加了互信息的下界

但是，我们不知道真实分布 q(C = 1|T, S)

相反，我们通过将模型 h : {T , S} → [0, 1] 拟合到数据分布 q(T, S|C = 1) 和 q(T, S|C = 0) 的样本来估计它，其中 T 和 S 表示嵌入的域

我们最大化该模型下数据的对数似然（二元分类问题）：

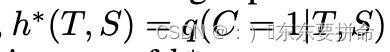
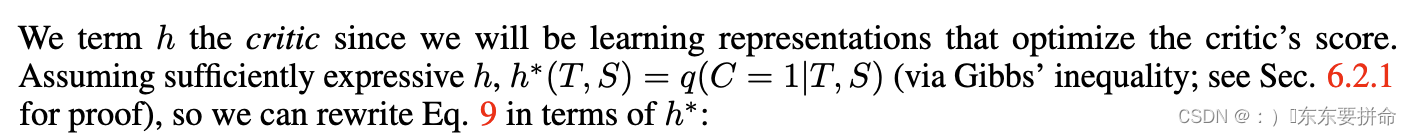
东东学到沉默 根本顶不住 

明天继续研究这个细节 我们继续

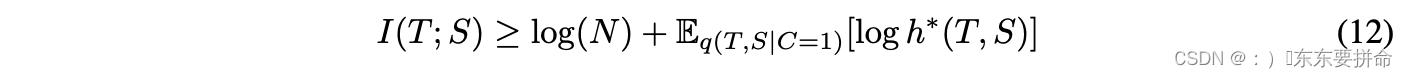
理解的挺抽象

因此，我们看到最优评价是一个期望下界互信息的估计量。

我们希望学习一个学生来最大化其表示和老师之间的互信息，提出以下优化问题：

The first line comes about by simply adding N Eq(T,S|C=0)[log(1 − h∗(T, S))] to the bound in (12) . This term is strictly negative, so the inequality holds. The last line follows from the fact that Lcritic(h∗)upper-bounds Lcritic(h). Optimizing (15) w.r.t. the student we have:

第一行是关于简单地将 N Eq(T,S|C=0)[log(1−h∗(T, S))] 添加到 (12) 中的界限。该术语严格为负，因此不等式成立。最后一行源于 Lcritic(h∗) 上限 Lcritic(h) 的事实。优化（15）w.r.t.我们有的学生：（太顶了 ）

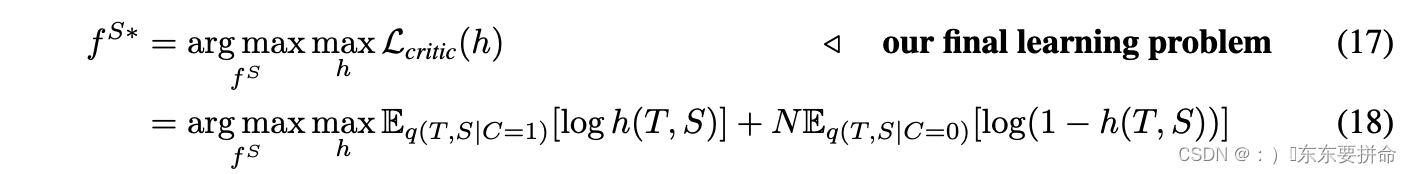
这表明我们可以同时学习 h 来联合优化 f S。

我们注意到，由于 (16) ，f S∗ = arg maxf S Lcritic(h)，对于任何 h，

也是对互信息优化下限（较弱的）的表示，因此我们的公式不依赖于 h 被完美优化。

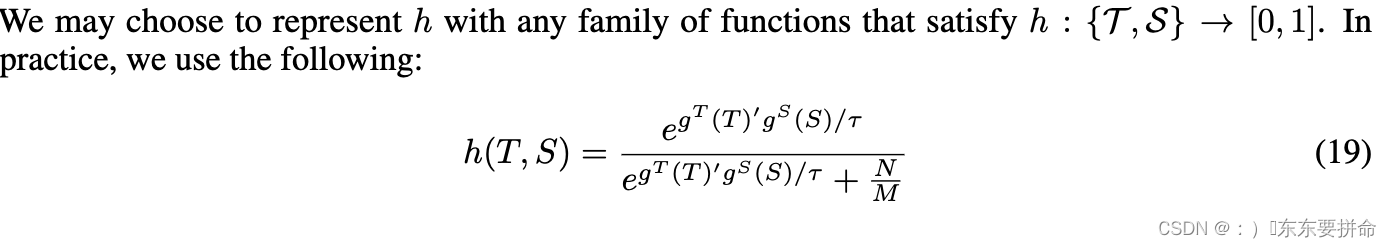
其中 M 是数据集的基数，τ 是调整浓度水平的温度。在实践中，由于 S 和 T 的维度可能不同，GS 和 gT 将它们线性变换为相同的维度，并在内积之前通过 L-2 范数进一步对其进行归一化。方程的形式。(18)的灵感来自于NCE(Gutmann&Hyvärinen，2010；Wu等人，2018)。我们的公式类似于 InfoNCE 损失 (Oord et al., 2018)，因为我们最大化互信息的下界。然而，我们使用了不同的目标和界限，在我们的实验中，我们发现它比 InfoNCE 更有效。

实施。理论上，方程式中的较大 N。 16 导致 MI 的下界更紧密。在实践中，为了避免使用非常大的批量大小，我们遵循 Wu 等人。 (2018) 并实现存储从先前批次计算的每个数据样本的潜在特征的内存缓冲区。因此，在训练期间，我们可以有效地从内存缓冲区中检索大量负样本。

今天就先这样吧 科研的孩子们晚安