堆（二叉树，带图详解）

news2024/9/27 9:23:36

一.堆

1.堆的概念

2.堆的存储方式

逻辑结构

 物理结构

2.堆的插入问题

3.堆的基本实现（代码）（以小堆为例）

1.堆的初始化

2. 向上调整

 3.插入结点

4. 交换函数、堆的打印

5.向下调整

 6.删除根节点并调整成小根堆

7.获取堆顶的元素

8.判断栈是否为空

9.另一种初始化数组的方法

10.两种实现堆排序的方法的比较

二、堆的应用与实现

1.堆的升序写法

 升序堆：

2.向下调整建堆(大堆)

总结

🗡CSDN主页：d1ff1cult.🗡

🗡代码云仓库：d1ff1cult.🗡

🗡文章栏目：数据结构专栏🗡

一.堆

1.堆的概念

如果有一个关键码的集合K = { ， ， ，…， }，把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中，并满足： <= 且
<= ( >= 且 >= ) i = 0，1，
2…，则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

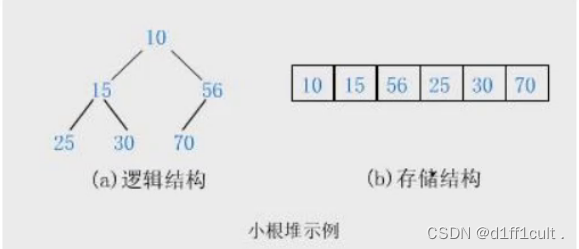
堆是一种非线性结构，是完全二叉树

堆分为小根堆（小堆）和大根堆（大堆）两种，小堆中所有的父节点均小于他的子结点，大堆中所有的父结点均大于子节点。

堆的底层用数组存储

小根堆：

大根堆：

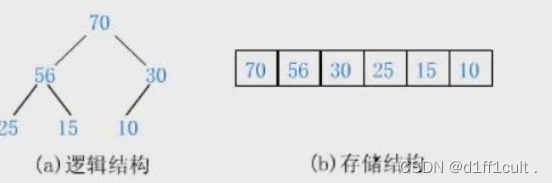
顺序存储下左右子树与父节点之间的关系：
leftchild=parent*2+1；

rightchild=parent*2+2；

parent=（child-1）/2;

2.堆的存储方式

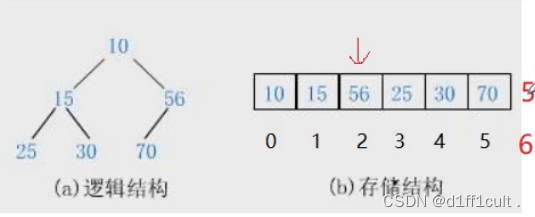
🗡逻辑结构

这里的逻辑结构是我们为了可以更好的李姐而想象出来的

 🗡物理结构

堆在内存中就是这样存储的

2.堆的插入问题

插入90我们发现该堆仍然是小堆，其实这是一个巧合，当我们插入50的时候发现该堆不再是一个小堆，我们此时需要不断地对50进行调整才能使得该堆重新成为小堆。

接下来继续向堆中插入一个5

插入数据后调整的基本思路:此时5的下标为6，根据5的下标找到5的父亲结点（5-1）/2=2 ，5的父亲结点为56，再让5与56比较大小，发现56>5所以将56和5的位置进行交换，再继续让交换后的5找父亲节点，5的父亲结点的下标为（2-1）/2=0，5的父亲结点为10，再将5与10继续比较，10>5进行交换，此时5的下标为0为根节点，调整完毕。

第一次进行交换:56与5进行比较 5<56 交换5和56

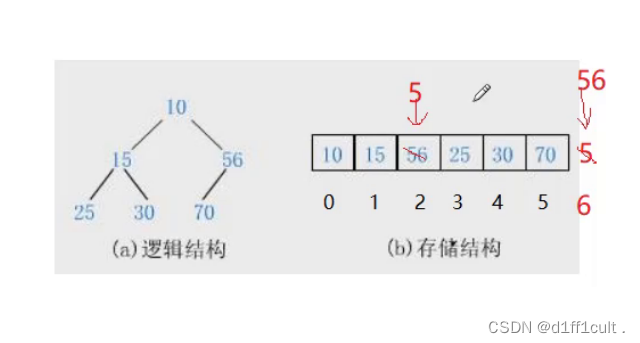
第二次进行交换： 找到交换后的5的父节点10，将10与5进行比较5<10则交换5与10的位置

 

很奇怪，这个最后插入的5 从孙子一跃成为了爷爷（bushi

3.堆的基本实现（代码）（以小堆为例）

下面介绍几个主要的实现堆的函数。

typedef int HPDataType;

typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;
void Swap(HPDataType* a, HPDataType* b);
void HeapPrint(HP* php);
void HeapInit(HP* php);
void HeapDestroy(HP* php);
void HeapPush(HP* php, HPDataType x);
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
void AdjustUp(HPDataType* a, int child);
void AdjustDown(HPDataType* a,int n,int parent);
bool HeapEmpty(HP* php);
void HeapInitArray(HP* php, int* a, int n);
void HeapSor

🗡堆的初始化

将数组和容量以及数组大小全部置空。

void HeapInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->capacity = 0;
	php->size = 0;
}

🗡向上调整

将插入的结点一步步调整，使该堆再次成为小堆

向上调整的前提：前面的数据是堆

AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child>0)
	{
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (parent - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

 🗡插入结点

插入一个结点，并将其调整成为一个小堆

void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{
		int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a,sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}
	php->a[php->size] = x;
	php->size++;
	AdjustUp(php->a, php->size-1);
}

🗡交换函数、堆的打印

void Swap(HPDataType* p1, HPDataType* p2)
{
	HPDataType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}//交换函数
void HeapPrint(HP* php)
{
	assert(php);
	for (int i = 0; i < php->size; i++)
	{
		printf("%d ", php->a[i]);
	}
	printf("\n");
}//堆的打印函数

🗡向下调整

向下调整的前提：根结点左右子树都是堆

void AdjustDown(HPDataType* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while(child<n)
	{
		if (child+1<n&&a[child] > a[child + 1])//保证child存的是左右孩子里面较小的那一个
		{
			++child;
		}

		if (a[child] < a[parent])// 父节点与两个儿子中较小的一个交换位置
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = child * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

🗡删除根节点并调整成小根堆

void HeapPop(HP* php)
{
	assert(php);  
	assert(php->size > 0);
	Swap(&php->a[0], php->a[php->size - 1]);
	--php->size;
	AdjustDowm(php->a, php->size, 0);
}

🗡获取堆顶的元素

HPDataType HeapTop(HP* php) 
{
	assert(php);
	assert(php->size > 0);
	return php->a[0];
}

🗡判断栈是否为空

bool HeapEmpty(HP* php)
 {
	 assert(php);
	 return php->size == 0;
 }

🗡另一种初始化数组的方法

 void HeapInitArray(HP* php, int* a, int n)
 {
	 assert(php);
	 assert(a);
	 php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);
	 if (php->a == NULL)
	 {
		 perror("malloc fail");
		 exit(-1);
	 }
	 php->size = n;
	 php->capacity = n;
	 memcpy(php->a, a, sizeof(HPDataType) * n); 
	 for (int i = 0; i < n; i++)
	 {
		 AdjustUp(php->a, i);
	 }
 }

🗡两种实现堆排序的方法的比较

 下面是使用HeapPush()函数实现堆排的过程  ：

void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child>0)
	{
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (parent - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{
		int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a,sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}
	php->a[php->size] = x;
	php->size++;
	AdjustUp(php->a, php->size-1);
}

这种方法是通过malloc函数开辟一块一块的空间，并通过不断地扩容将数据push到数组中，再对数组中的内容进行不断的向上调整从而达到堆排的目的。

下面是用AdjustUp()函数实现堆排的过程：

void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child>0)
	{
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (parent - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
void HeapSort(int* a, int n)
{
	for (int i = 0; i < n; i++)
	{
		AdjustUp(a, i);
	}
}

这种方法与HeapPush函数不同的地方在于该函数传参数时直接传入一个数组，省去了malloc开辟空间的消耗。

二、堆的应用与实现

🗡堆的升序写法

通常这里我们都会问一个问题，实现升序排序我们应该建一个小堆还是一个大堆？

答案是，升序时我们应该建一个大堆，那么为什么呢？

我们都知道小堆的根节点是整棵二叉树中最小的值，选出了最小的值之后，我们还要去找次小的值

 首先是建小堆不适用的原因，这里有这样一个数组，我们将这个数组展开：

 

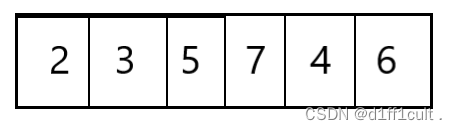
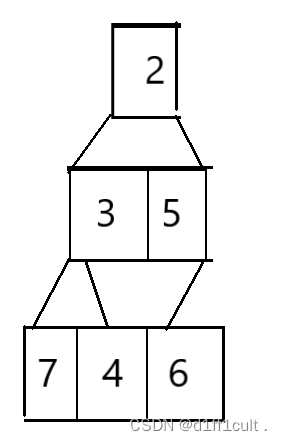
 按照我们需要建升序堆的要求，我们会将最小的根节点删除掉，删除后如下图所示

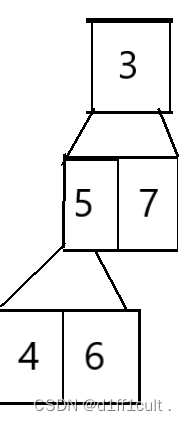
我们发现这个二叉树不再是堆，但是我们要选择次小值的话需要进行调整，就需要重新建堆，建堆的时间复杂度为o(n)=n*logn,代价还是比较大的，甚至不如遍历一遍来的快，所以我们这里摒弃了建小堆的想法，那么接下来就看看建大堆的优势在哪里了

 建大堆的基本思想以及优势:

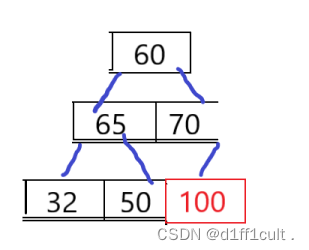
我们排升序，建一个大堆，将根节点和最后一个结点交换位置，那么最大的数就被交换到了数组的最后面，此时一个数字已经排好了，原本根节点的左右子树还是堆，我们就可以通过向下调整，来找出次打的值，此时我们不再把交换到数组最后的根节点看作树的结点，对剩下的数字进行向下调整，找出了次小的值，这里的时间复杂度O(n)仅仅为logn合计起来n个结点的时间复杂度O(n)=n*logn，消耗比较小。再与树的最后一个结点进行交换。过程我们用下面的数组进行演示。

 

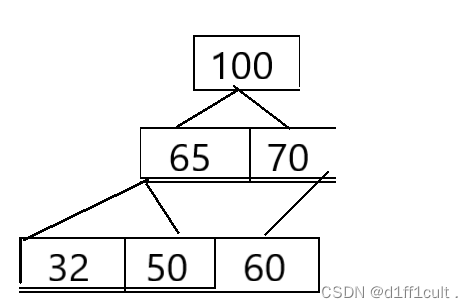
将根节点的数字与树的最后一个结点的数字进行交换，并不再把交换到后面的根节点看作树的内容

 🗡升序堆：
void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child>0)
	{
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (parent - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
void AdjustDown(HPDataType* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while(child<n)
	{
		if (child+1<n&&a[child] > a[child + 1])//保证child存的是左右孩子里面较小的那一个
		{
			++child;
		}

		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = child * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapSort(int* a, int n)
{
	for (int i = 0; i < n; i++)
	{
		AdjustUp(a, i);
	}
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		--end;
	}
}

🗡向下调整建堆(大堆)

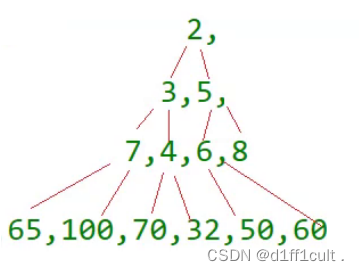
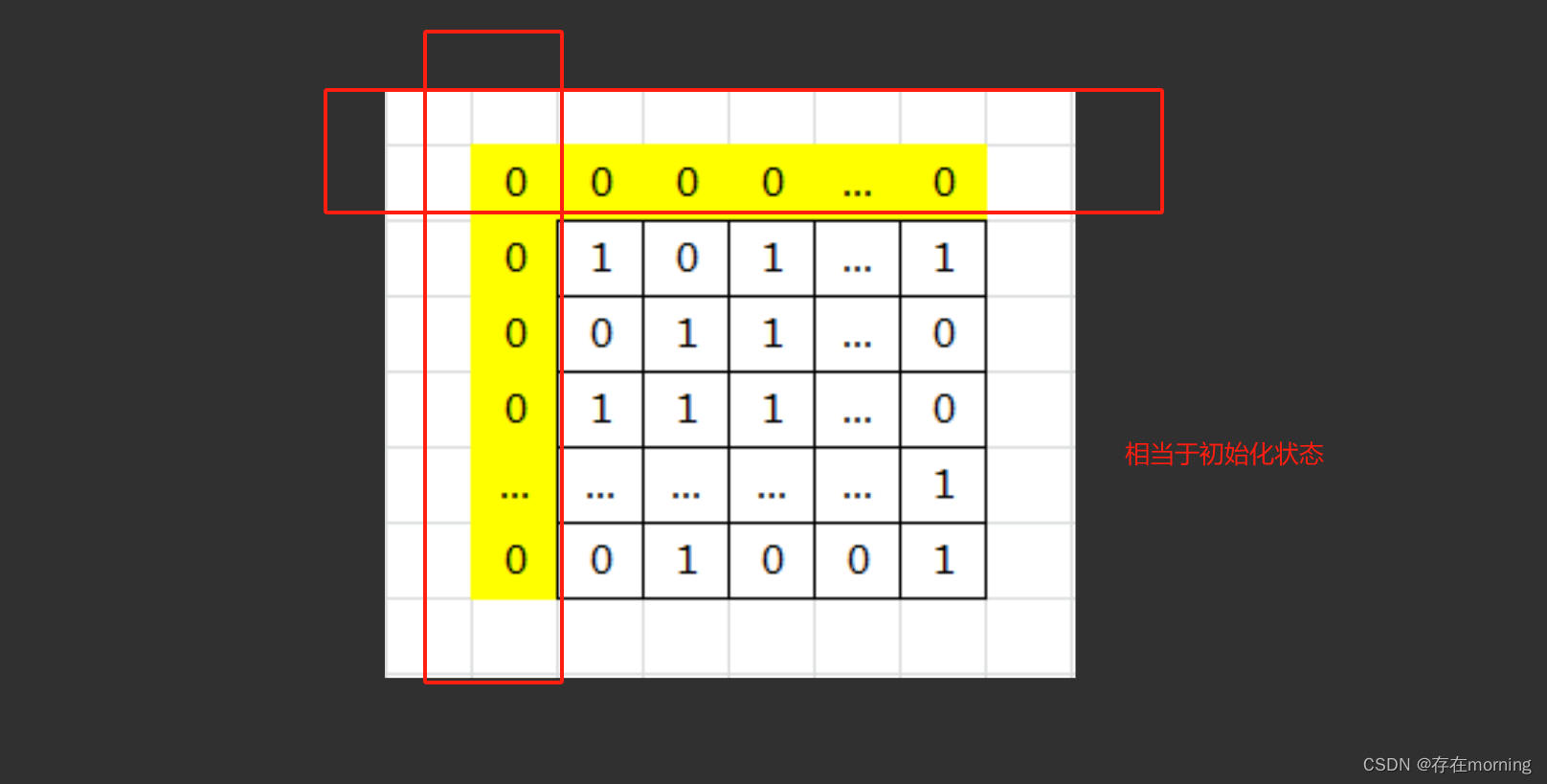
有这样一个数组，我们如果想通过用根节点直接向下调整建大堆，就必须保证根节点的左右子树都是大堆，所以我们就想出了倒着调整树的方法：

需要注意的是：单个叶子结点，既是大堆也是小堆。

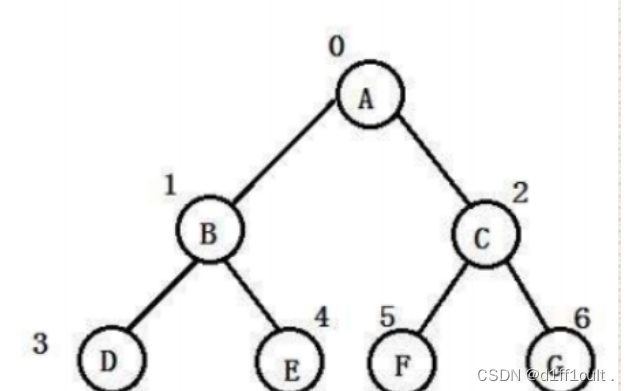
这种建堆方法是从树的末尾开始找到第一个非叶子结点然后对其进行向下调整，从数组后面查找的第一个非叶子结点也就是树中最后一个结点的父节点，最后一个结点的下标为n-1，则它的父结点的下标为(n-1-1)/2 ，这棵树从后面查找的第一个非叶子结点是6，对6进行向下调整，如下图

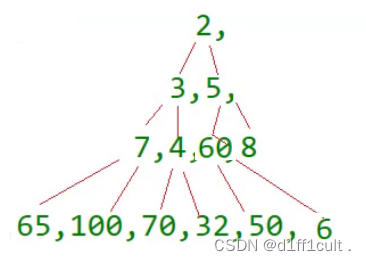
我们发现调整完成之后，结点5的左子树已经成为了大堆，右子树也是大堆，那我们就应该对下一个非叶子结点进行调整了，我们只需要将60位置的下标+1，就得到了下一个非叶子结点的下标，同理也对他进行调整，直到2的左右子树都调整为大堆

void AdjustDown(HPDataType* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while(child<n)
	{
		if (child+1<n&&a[child] > a[child + 1])//保证child存的是左右孩子里面较小的那一个
		{
			++child;
		}

		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = child * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapSort(int* a, int n)
{
	//向上调整建堆（大堆或者小堆）
	//for (int i = 0; i < n; i++)
	//{
	//	AdjustUp(a, i);
	//}
	//向下调整建堆
	for (int i = (n - 2) / 2; i >= 0; i--)
	{
		AdjustDown(a, n, i);
	}
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		--end;
	}
}

向上调整建堆，时间复杂度O(n)=n*logn，而向下调整建堆的时间复杂度O(n)=n.

总结

上述就是关于堆的一些知识，有不懂的地方欢迎提问。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1133467.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Transformer详解学习

Transformer详解学习

1. Transformer 原理 1.1 Transformer整体结构 Transformer的结构图&#xff0c;拆解开来&#xff0c;主要分为图上4个部分&#xff0c;其中最重要的就是2和3Encoder-Decoder部分&#xff0c;对咯&#xff0c;Transformer是一个基于Encoder-Decoder框架的模型。 接下来我将按照…
阅读更多...
通过使用Cpolar内网穿透工具实现BUG管理系统的远程访问

通过使用Cpolar内网穿透工具实现BUG管理系统的远程访问

文章目录 前言1. 本地安装配置BUG管理系统2. 内网穿透2.1 安装cpolar内网穿透2.2 创建隧道映射本地服务 3. 测试公网远程访问4. 配置固定二级子域名4.1 保留一个二级子域名 5. 配置二级子域名6. 使用固定二级子域名远程7. 结语 前言 BUG管理软件,作为软件测试工程师的必备工具…
阅读更多...
Kettle循环结果集中的数据并传入SQL组件【或转换】里面

Kettle循环结果集中的数据并传入SQL组件【或转换】里面

简介&#xff1a;在尝试使用了结果集的Demo循环后&#xff0c;进入到生产还是有一点问题的&#xff0c;以下是各个组件的分解解释、遇到的问题&#xff0c;以及解决问题的思路&#xff0c;最后文章的最后会把完整的Ktr文件放出来。记得收藏点赞喔&#xff01; 先来看张图~来自…
阅读更多...
【疯狂Java】数组

【疯狂Java】数组

1、一维数组 (1)初始化 ①静态初始化&#xff1a;只指定元素&#xff0c;不指定长度 new 类型[] {元素1,元素2,...} int[] intArr; intArr new int[] {5,6,7,8}; ②动态初始化&#xff1a;只指定长度&#xff0c;不指定元素 new 类型[数组长度] int[] princes new in…
阅读更多...
【德哥说库系列】-PostgreSQL跨版本升级

【德哥说库系列】-PostgreSQL跨版本升级

&#x1f4e2;&#x1f4e2;&#x1f4e2;&#x1f4e3;&#x1f4e3;&#x1f4e3; 哈喽&#xff01;大家好&#xff0c;我是【IT邦德】&#xff0c;江湖人称jeames007&#xff0c;10余年DBA及大数据工作经验 一位上进心十足的【大数据领域博主】&#xff01;&#x1f61c;&am…
阅读更多...
【算法训练-动态规划 五】【二维DP问题】最大正方形

【算法训练-动态规划 五】【二维DP问题】最大正方形

废话不多说&#xff0c;喊一句号子鼓励自己&#xff1a;程序员永不失业&#xff0c;程序员走向架构&#xff01;本篇Blog的主题是【动态规划】&#xff0c;使用【数组】这个基本的数据结构来实现&#xff0c;这个高频题的站点是&#xff1a;CodeTop&#xff0c;筛选条件为&…
阅读更多...
Kafka - 深入了解Kafka基础架构：Kafka的基本概念

Kafka - 深入了解Kafka基础架构：Kafka的基本概念

文章目录 Kafka的基本概念 Kafka的基本概念 我们首先了解一些Kafka的基本概念。 1&#xff09;Producer &#xff1a;消息生产者&#xff0c;就是向kafka broker发消息的客户端2&#xff09;Consumer &#xff1a;消息消费者&#xff0c;向kafka broker获取消息的客户端3&…
阅读更多...
如何避免Web3诈骗，重点关注这5个安全标识提醒

如何避免Web3诈骗，重点关注这5个安全标识提醒

从预付费电子邮件到网络钓鱼攻击&#xff0c;互联网充斥着各种骗局。尽管区块链内置了加密功能&#xff0c;但它们也遭受了相当多的恶意攻击并被获取了对帐户的访问权限。幸运的是&#xff0c;大多数诈骗攻击都有特定的安全标识提醒&#xff0c;精明的用户可以留意&#xff0c;…
阅读更多...
淘宝商品详情API接口，解决滑块问题

淘宝商品详情API接口，解决滑块问题

淘宝商品详情API接口是一种用于获取淘宝商品详细信息的接口&#xff0c;它可以帮助开发者在自己的网站或应用程序中快速获取淘宝商品的详细信息&#xff0c;包括价格、图片、商品描述等。 该接口的主要作用包括&#xff1a; 商品信息展示&#xff1a;通过淘宝商品详情API接口…
阅读更多...
网络协议--IGMP：Internet组管理协议

网络协议--IGMP：Internet组管理协议

13.1 引言 12.4节概述了IP多播给出&#xff0c;并介绍了D类IP地址到以太网地址的映射方式。也简要说明了在单个物理网络中的多播过程&#xff0c;但当涉及多个网络并且多播数据必须通过路由器转发时&#xff0c;情况会复杂得多。 本章将介绍用于支持主机和路由器进行多播的In…
阅读更多...
wkhtmltoimage/wkhtmltopdf 使用实践

wkhtmltoimage/wkhtmltopdf 使用实践

1. 介绍 wkhtmltopdf/wkhtmltoimage 用于将简单的html页面转换为pdf或图片&#xff1b; 2.安装 downloads 2.1. mac os 下载64-bit 版本然后按照指示安装, 遇到 untrust developers 时&#xff0c;需要在 Settings -> Privacy 处信任下该安装包。 2.2. debian # 可用…
阅读更多...
[AutoSar NVM] 存储架构

[AutoSar NVM] 存储架构

依AutoSAR及公开知识辛苦整理&#xff0c;禁止转载。 专栏 《深入浅出AutoSAR》&#xff0c; 全文 2900 字. 图片来源&#xff1a; 知乎 汽车的ECU内存中有很多不同类型的变量&#xff0c;这些变量包括了车辆各个系统和功能所需的数据。大部分变量在ECU掉电后就会丢失&#x…
阅读更多...
AnkiPDF Guru软件评测：打开全新学习方式的大门

AnkiPDF Guru软件评测：打开全新学习方式的大门

在当今信息爆炸的时代&#xff0c;如何高效学习和记忆成为了每个人关注的焦点。AnkiPDF Guru软件作为结合了Anki和PDF的学习利器&#xff0c;向我们展示了一种全新的学习方式。本文将以软件的实用性和使用场景为切入点&#xff0c;从专业的角度客观分析和评测该软件&#xff0c…
阅读更多...
3.2.6:工作表的VBA操作引申

3.2.6:工作表的VBA操作引申

我给VBA的定义&#xff1a;VBA是个人小型自动化处理的有效工具。利用好了&#xff0c;可以大大提高自己的劳动效率&#xff0c;而且可以提高数据处理的准确度。我推出的VBA系列教程共九套和一部VBA汉英手册&#xff0c;现在已经全部完成&#xff0c;希望大家利用、学习。 如果…
阅读更多...
【毕业设计】基于SSM酒店后台管理系统

【毕业设计】基于SSM酒店后台管理系统

前言 &#x1f525;本系统可以选作为毕业设计&#xff0c;运用了现在主流的SSM框架&#xff0c;采用Maven来帮助我们管理依赖&#xff0c;所选结构非常合适大学生所学的技术&#xff0c;本系统结构简单&#xff0c;容易理解&#xff01;本系统功能结构完整&#xff0c;非常高适…
阅读更多...
express session JWT JSON Web Token

express session JWT JSON Web Token

了解 Session 认证的局限性 Session 认证机制需要配合 cookie 才能实现。由于 Cookie 默认不支持跨域访问&#xff0c;所以&#xff0c;当涉及到前端跨域请求后端接口的时候&#xff0c;需要做很多额外的配置&#xff0c;才能实现跨域 Session 认证。 注意&#xff1a; 当前端…
阅读更多...
rust学习—— 复合类型结构体、复合类型枚举、复合类型元组

rust学习—— 复合类型结构体、复合类型枚举、复合类型元组

文章目录 复合类型元组用模式匹配解构元组用点来访问元组元组的使用示例 复合类型结构体结构体定义结构体语法创建结构体实例访问结构体字段简化结构体创建结构体更新语法 结构体的内存排列元组结构体(Tuple Struct)单元结构体(Unit-like Struct)结构体数据的所有权打印结构体 …
阅读更多...
k8s kubeadm配置

k8s kubeadm配置

master 192.168.41.30 docker、kubeadm、kubelet、kubectl、flannel node01 192.168.41.31 docker、kubeadm、kubelet、kubectl、flannel node02 192.168.41.32 do…
阅读更多...
springboot配置redis

springboot配置redis

1.Jedis库 依赖库 <dependency><groupId>redis.clients</groupId><artifactId>jedis</artifactId><version>5.0.2</version> </dependency>使用案例&#xff1a; Testpublic void jedis(){Jedis jedis new Jedis("127…
阅读更多...
【Java 进阶篇】Java Servlet URL Patterns 详解

【Java 进阶篇】Java Servlet URL Patterns 详解

Java Servlet 是构建动态 Web 应用程序的关键组件之一&#xff0c;而 URL Patterns&#xff08;URL 模式&#xff09;则是定义 Servlet 如何响应不同 URL 请求的重要部分。在本文中&#xff0c;我们将深入探讨 Java Servlet URL Patterns 的各个方面&#xff0c;适用于初学者&a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023